1. 引言
在高超声速风洞中,大多采用带有尾支撑的强迫振动法开展动导数实验 [1] 。支撑干扰是动导数误差的重要来源,其对模型气动力影响的严重程度远超过洞壁干扰效应。在高超声速风洞中尾支干扰主要体现在对阻力特别是底部阻力测量的干扰,而底部阻力修正是高超声速风洞试验一直没有很好解决的问题。针对钝锥的初步研究表明,尾支撑对钝锥动态气动力的影响远超过静态的情况 [2] ,当涉及到激波诱导分离、旋涡运动与破裂等非定常流动结构产生非线性气动载荷时,动态条件下的支撑干扰的研究是一项难度大,技术复杂的课题。而对于动导数这类特种实验,尚未有过系统的支撑干扰修正研究。目前在我国高超声速飞行器技术飞速发展的大背景下,对于高超声速复杂飞行器来说,特别是包含内流的机体推进一体化飞行器,迫切需要针对动导数特种实验开展支撑干扰研究 [3] 。
支撑干扰的修正主要包括试验修正方法、工程修正方法和数值计算方法。试验修正方法采用辅助支架和叠加法来测定主(假)支撑的干扰,该方法已使用多年,不论什么类型支撑系统,不论高、低速风洞,不论静、动态试验,均采用叠加法测定支撑干扰,但在实践中发现在某些情况下测量值并不合理,这往往发生在分离流、大扰动或非定常流动现出现时 [4] 。文献 [5] 综述了在静态试验和动态试验研究支架干扰的情况,G. S. Taylor等通过水洞试验研究三角翼的动态支架干扰 [6] ,结果显示出动态非定常条件下的动导数支撑干扰的试验修正方法成本高,试验条件的限制较多,并且一般采用辅助支撑带虚拟支杆的方法进行支撑干扰修正,难以扣除二次干扰 [7] 。
工程修正方法有较大的局限性,当试验模型和支架形式与已知支架干扰的模型和支架形式相差甚远时工程修正方法并不可靠。文献 [8] 提出高速尾撑干扰的工程估算修正方法。尾撑系统对常规测力模型的升力干扰很小,可以不修正。支杆对模型阻力的影响主要是对模型后体阻力的影响,它取决于模型后体的几何形状、支杆的几何参数、来流马赫数和雷诺数。但对于动态非定常条件下的动导数等特种试验,尚未有可靠的工程估算方法 [9] 。
考虑了流动非线性、非定常效应的数值计算方法精度高,不受模型运动等干扰因素的影响,是支撑干扰的修正的重要发展方向 [10] 。目前大多数研究采用数值计算方法开展常规静态气动力的支撑干扰修正,针对动导数特种实验的系统性支撑干扰修正研究较为少见 [11] 。本文采用三维非定常N-S方程针对类X-51A吸气式高超声速内外流一体化飞行器的动导数辨识开展支撑干扰数值模拟研究。在7˚钝锥标模验证的基础上,对比类X-51A动导数试验模型与真实飞行条件下的动态特性,开展尾支撑干扰对动导数的影响研究,获得尾支撑干扰带来的动导数变化量。
2. 数值方法
在贴体坐标系下,对完全气体、忽略质量力下的三维无量纲Navier-Stokes方程形式如下:
(1)
式中:
为守恒变量,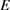 、
、
为无粘通量,
、
、
为粘性通量。
、
、
为无粘通量,
、
、
为粘性通量。
本文在空间上采用二阶精度的Roe格式,Roe格式是基于Godunov方法的基本思路发展起来的,是通量差分分裂(FDS)格式的一种,由于其优秀的间断分辨率和较小的数值耗散性,目前受到广泛的应用。采用引入“双时间步”(Dual-time-step)方法的LU-SGS隐式格式离散流体运动方程时间项。动网格生成采用刚性网格生成方法。远场入流边界采用适用于动态边界条件下的一维Riemann不变量的无反射边界条件。对于定常/非定常超音速出流,边界点上的值由内流场计算结果外推得到。对于壁面边界,采用速度无滑移、绝热壁条件。奇性轴采用外插后周向平均处理。
3. 动导数计算方法
在飞行器姿态控制系统设计及轨道(弹道)设计中,所需要的动态稳定性参数有数十个之多 [12] 。表1列出了一些重要的动态阻尼导数。本文采用小振幅强迫简谐分析法给出了多种导数的数值辨识方法 [13] 。

Table 1. Dynamic damping derivatives
表1. 动态阻尼导数 [14]
对于飞行器做单自由度的俯仰运动,如果其质心速度不变,则确定运动的独立状态变量只有攻角
和俯仰角速度
。对俯仰力矩系数
,由Etkin假定,俯仰力矩系数可写成:
(2)
给定强迫振动:
,其中
为瞬时攻角,
为俯仰角,
为基准状态的攻角,
为振动幅度,k为减缩频率。在k不很大,且忽略高阶导数的影响时,当非定常振动过程达到谐振解,通过数值积分可以求出俯仰阻尼导数为 [15] :
(3)
式中:
为积分起始时刻,
为振动周期。
类似的,通过给定不同的扰动方式可以推导出其他类型的动态稳定性参数的计算公式。其中强迫滚转运动的形式为
,
为滚转角,
为滚转角振幅;强迫偏航运动的形式为
,
为偏航角,
为偏航角振幅。
4. 验证算例
验证算例选自美国阿诺德工程发展中心冯·卡门空气动力学实验室(AEDC-VKF) 7˚钝锥的支撑干扰实验 [16] 。实验来源于一个为期三年的技术项目,目的是获得系统的超声速、高超声速风洞实验的支撑干扰特性。7˚钝锥的支撑干扰实验测量了尾支撑长度对动导数、静态俯仰力矩系数及底部压力的影响,同时对马赫数、攻角、边界层流态、减缩频率等影响因素进行了细致的考察。

Figure 1. Blunt cone dimensions and centroid position
图1. 钝锥外形尺寸及质心位置

Figure 2. Two forms of support for the blunt cone
图2. 钝锥外形的两种支撑形式

Figure 3. Comparison of moment coefficients of two support forms
图3. 两种支撑形式力矩系数的对比
图1给出了钝锥的外形尺寸及质心位置。实验分为两种不同的支撑形式,如图2。第一种形式的支撑(Interference Sting, IS)支杆长度Ls与底部直径D长度相等,使得支撑与底部流场之间存在较强的干扰,第二种形式的支撑(Clean Sting, CS)支杆长度Ls是底部直径D的3.3倍,由于支杆相对较长,使得干扰效应相对较弱。
马赫数为2、5、8的实验结果和马赫数为5的计算结果均显示出两种支撑形式的静态俯仰力矩基本相同,而动态条件下的俯仰阻尼导数却存在很大差异,如图3所示。实线为俯仰力矩系数结果,虚线为俯仰阻尼导数结果。由此可见,当涉及到激波诱导分离、旋涡运动与破裂等非定常流动结构产生非线性气动载荷时,动态条件下的支撑干扰远比静态条件下复杂,静态条件下的支撑干扰修正规律不能直接应用于动态非定常的情况。
图3(d)给出了马赫数为5的条件下本文计算结果与实验的对比,俯仰力矩系数的差别不超过10%,俯仰阻尼导数的差别不超过30%,较好的验证了本文动态非定常计算的可靠性。
5. 类X-51A支撑干扰计算
高超声速巡航导弹X-51A是美国空军研究实验室(AFRL)联合波音公司(负责机身)和普惠公司(负责发动机)研制的一架超燃冲压发动机验证机—乘波器(SED-WR)飞行试验平台。本文以内外流一体化飞行器X-51A为背景,利用公开的图像数据资料进行反向建模,生成的类X-51A三维实体外形见图4。飞行器全长4.2672 m (168 inches),最大体宽度0.5842 m (23 inches),进气道宽度0.2286 m (9 inches)。图5给出了内流道的示意图。燃烧室凹腔为开式凹腔,长度为0.1193 m,深度为0.0178 m,长深比6.7,后缘角为30度。带支杆的实验外形如图6所示。模型缩比为1:10,支杆长度0.3833 m,支杆安装角为1˚。

Figure 4. X-51-like hypersonic vehicle
图4. 类X-51高超声速飞行器
本文模拟的飞行状态为马赫数4.8,飞行高度18,288公里(60,000英尺)。此时助推器与飞行器分离,进气道打开,发动机尚未点火,内流道处于冷流状态下的通流状态。带支杆的实验外形的计算状态为马赫数4.8,来流温度60 k,来流压力412.9 Pa。表2为真实外形与带支杆的实验外形0度攻角下定常计算结果的对比。设计工况下类X-51A外形的俯仰力矩处于配平状态,受支撑干扰影响实验外形产生了小的低头力矩,升力系数和阻力系数也有明显的差别。表中还给出了进气道性能参数之间的对比。从图7进气道波系结构的对比来看,真实飞行状态与缩比模型实验状态的天地不一致是造成二者差异的主要原因。受模型缩比的影响,真实外形的压升比和温升比低于缩比外形,流量系数、总压恢复系数及进气道出口的平均马赫数高于缩比外形,进气道内存在更为清晰的激波反射过程。

Table 2. Comparison between the real shape and the experi-mental shape
表2. 真实外形与实验外形对比
在定常模拟的基础上,本文开展了动态非定常流场的计算,得到了真实外形的俯仰阻尼导数
为−0.968,缩比实验外形为−0.962,静态计算时二者升力系数差别为16%,阻力系数差别达到24%,但动态情况下动导数的差别不超过千分之七,说明了静态条件下的支撑干扰修正规律与动态非定常的情况完全不同。图8展示了动态条件下俯仰力矩系数及进气道性能参数的迟滞特性。真实外形与实验外形的各项进气道性能参数有较大偏移,迟滞环形状也不尽相同,但二者俯仰力矩系数迟滞环却差别不大,充分说明了非线性非定常主导的流动特征往往会给飞行器带来超出预期的气动效应。

Figure 7. Schlieren photograph of inlet symmetry plane
图7. 进气道对称面数值纹影图

Figure 8. Pitch moment coefficient and inlet performance parameters loop
图8. 俯仰力矩系数及进气道性能参数迟滞环
6. 结论
本文采用三维非定常N-S方程针对类X-51A吸气式高超声速内外流一体化飞行器的动导数辨识开展支撑干扰数值模拟研究。针对钝锥俯仰方向的验证算例显示,不同支撑形式下的静态力矩系数基本相同,而动态阻尼导数却存在很大差异。针对类X-51A真实外形与实验外形的比较显示,静态条件下气动力/力矩系数与进气道性能参数有显著差异,但动态条件下的俯仰力矩系数及俯仰阻尼导数却基本一致。因此对俯仰阻尼导数来说,动态非定常条件下的支撑干扰修正规律与静态的情况完全不同。要想获得系统的类X-51A内外流一体化外形支撑干扰特性,后续应进一步开展滚转和偏航方向上的直接阻尼导数和交叉阻尼导数的支撑干扰研究。此外,还需要开展不同攻角、马赫数以及考虑尾喷管喷流效应等更多工况的数值模拟研究。