1. 引言
软管式空中加油具有成本低且方式简单的特点,是目前空中加油领域应用最为广泛的加油方式。但是软管式空中加油系统的缺点也十分明显,加油机吊舱拖拽着软管–锥套飞行时受到大气紊流的干扰会造成飘摆运动,这对受油机的准确对接产生影响,严重的情况可能会造成机毁人亡,因此对软管–锥套的飘摆运动进行建模与控制对保证空中加油系统安全性有着十分重要的意义。
在软管–锥套系统中,锥套提供的阻力通常占据总阻力的75%以上 [1] ,改变锥套的伞面面积可以有效改变锥套提供的阻力大小,进而控制锥套下沉或者上升达到锥套位置可控的目的。
目前,国内外学者有关软管–锥套的建模和控制的研究已取得显著的成果,北京航空航天大学的王海涛等人 [2] 提出了一种变长度多级串联理想单摆系软管运动模型,针对对接过程的软管飘摆运动现象设计了积分滑膜反推控制器。南京航空航天大学的张进等人 [3] 建立了加油软管–锥套数学模型,并设计了PID控制器用于抑制系统受到大气紊流影响产生的飘摆运动,从而降低软管摆动的幅度。
国外williamson [4] 研究了一种通过改变稳定伞阻尼系数对锥套产生主动控制的方法,并通过风洞实验确定了模型参数,设计了LQR控制器。
国内外现有关于软管–锥套系统的研究文献大多采用经验值进行系统建模,而没有对锥套气动特性的影响因素如伞撑角、伞撑厚度等进行深入探讨,并进行仿真分析。本文以研究软管–锥套系统动态特性为基础,主要采用CFD模拟技术对一类变阻尼稳定伞进行气动分析,然后通过建立稳定伞的模型并将模型在模拟风场的环境下进行仿真分析,最后确定伞撑角与作用在稳定伞上的气动力大小的关系。
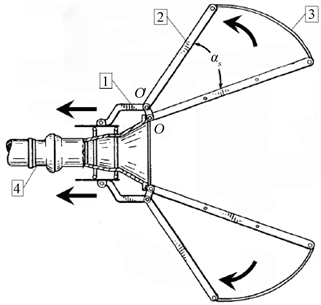
Figure 1. Structural sketch of a variable damping stabilization umbrella
图1. 某型变阻尼稳定伞结构示意图
2. 变阻尼稳定伞设计及伞面形状的确定
本文所参考变阻尼稳定伞设计为文献 [5] 中的设计,如图1所示,某型稳定伞变阻尼结构如图所示,伞撑的开合程度用伞撑角
表示,即为图中内外两个撑杆之间的夹角,2为稳定伞的可活动伞骨,装置1向左活动时带动OO’绕定点O绕动,2的一端与O’相连带动伞骨2张开,即伞撑角
变大,伞面的阻尼增加,稳定伞下沉量增加。同理,装置1向右移动时,伞骨2收缩,伞撑角
变小,伞面的阻尼减少,稳定伞下沉量减少。这就是变阻尼稳定伞的设计思想,通过改变伞撑角
的大小控制稳定伞的阻尼大小,从而达到控制稳定伞位置的目的。
稳定伞面采用透气的尼龙织物材料,在没有风场的情况下,伞面没有确定的形状,在处于风场的情况下,伞面的形状由来流速度和伞撑角等因素有关,然而伞面形状与这些影响因素没有确定的关系形式。但是,可以确定的是不同的伞面形状有着不同的伞背面的尾流形态和流动分离点,因此,不同的伞面形状对稳定伞的气动模型有不同的影响。
3. CFD数值模拟
3.1. 稳定伞模型
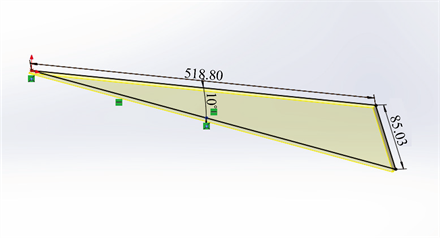
稳定伞的伞面材料一般采用柔软可透气的尼龙织物,在无风的状态下,伞面没有固定的形状,在风场中的稳定伞伞面形状与来流速度和伞撑角有关。因此为了建立稳定伞模型,假设伞面材料无弹性,在风场的作用下,伞面不可延伸。稳定伞模型采用SolidWorks软件搭建,其模型尺寸与实际尺寸相当见图2。伞撑采用36个等圆周分布,伞撑厚度为8 mm,伞面厚度为6 mm。
把SolidWorks搭建的模型导入fluent进行网格划分,将稳定伞处于的外流场建立为圆柱体计算域:D = 10 m,L = 20 m (见图3)。将三种型号的模型(见图4)分别放入流场中模拟,模拟来流为定常、可压缩、3-D粘性假设的理想气体,湍流模型选取常用的S-A模型,来流速度从200 km/h增加到600 km/h,步长为100 km/h。数值迭代直至稳定,监测阻力值也趋于稳定,收敛精度达10−4。
3.2. 仿真结果分析
理论上分析伞面厚度以及透气性会影响模拟的结果,仿真的目的是为了模拟真实的情况伞阻力大小,通过对比仿真结果和真实的实验数据即可验证仿真结果是否可信,本文给出某型锥套的仿真模型及仿真数据,与飞行试验数据进行对比,该试验数据为NASA德莱顿飞行试验中心 [6] 。
 (a)
(a) 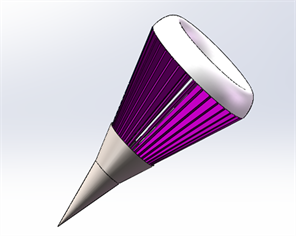 (b)
(b)
Figure 2. (a) 10-degree umbrella support size; (b) SolidWorks model of paradrogue
图2. (a) 10度伞撑尺寸;(b) 锥套SolidWorks模型

Figure 3. The computational domain of steady parachute flow field
图3. 稳定伞流场计算域
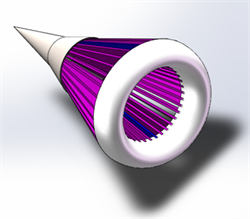 (a) αs = 10˚
(a) αs = 10˚  (b) αs = 20˚
(b) αs = 20˚  (c) αs = 30˚
(c) αs = 30˚
Figure 4. The shape of three conical sleeve stabilized parachutes
图4. 三种锥套稳定伞外形
德莱顿飞行试验中心的飞行试验在在7500 ft和2100 ft~2900 ft的高空进行,本文的CFD模拟仿真采用标准大气模型,高度定为1300 ft,在大气对流层有公式可以描述标准大气模型的温度、压力和密度之间的关系:
(1)
(2)
(3)
式中,
、
、
取海面标准值,温度为15℃对应
= 288.15 K,
= 101,325 Pa,
= 1.225 kg/m3。
图5为飞行试验结果和仿真数据对比,对比图中数据可以得出CFD仿真结果(红色数据点)和试验结果拟合直线相近,证明仿真结果是可信的。
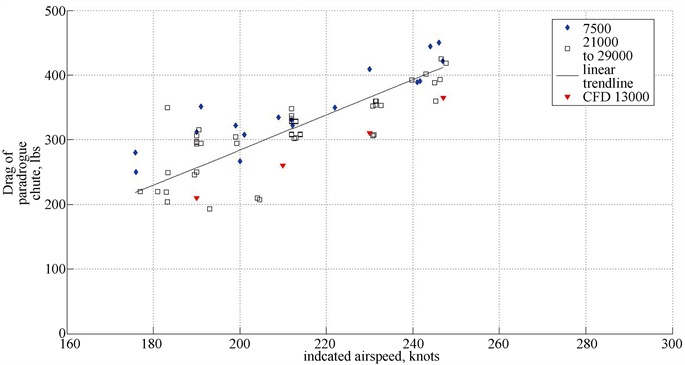
Figure 5. Comparison of CFD simulation results with flight test data
图5. CFD模拟结果与飞行试验数据对比
4. 模拟结果与分析
分析稳定伞背风截面流线图(见图6)可知,稳定伞的伞撑角为10˚时几乎没有背风面分离气泡,而随着伞撑角的增大,背风面分离气泡增大,这意味着稳定伞阻力也随之增加,若Cd记为稳定伞的阻力系数,则稳定阻力D可表示为 [7] [8] :
(4)
其中,
、
、
分别表示来流密度、速度及参考面积。Cd与
、
的关系可表示为:
(5)
图7为Cd与
的关系曲线,分析可知,Cd在一定来流速度范围内,Cd受
影响较小,因此上式近似变式为:
(6)
伞撑角
的改变,实际是改变伞面阻力面积,阻力面积与伞撑角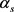 的平方有正比关系,即有Cd与
的关系式如下所示:
的平方有正比关系,即有Cd与
的关系式如下所示:
(7)
其中,系数A、B、C为待定系数,
取10˚、20˚、30˚,Cd取0.65、0.71、0.83 [9] 代入可得:
(8)
经过以上分析可以得出稳定伞的阻力系数随着伞撑角的增大而增大,也即是稳定伞的阻力随伞撑角的增大而增加。根据软管-锥套系统模型 [10] 可知,锥套的位置随着气动载荷的变化,锥套随之上浮或下沉,参考图8可以通过改变伞撑角的大小,进而改变稳定伞的阻力大小,从而有助于软管–锥套系统的控制部分优化,应对其飘摆运动。
 (a)
= 10˚
(a)
= 10˚ 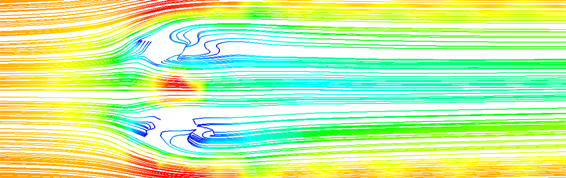 (b)
=20˚
(b)
=20˚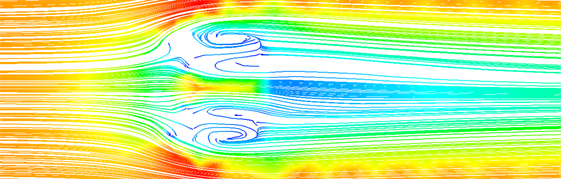 (c)
= 10˚
(c)
= 10˚
Figure 6. Ma = 0.5, streamline diagram of leeward section of stable umbrella
图6. Ma = 0.5,稳定伞背风截面流线图
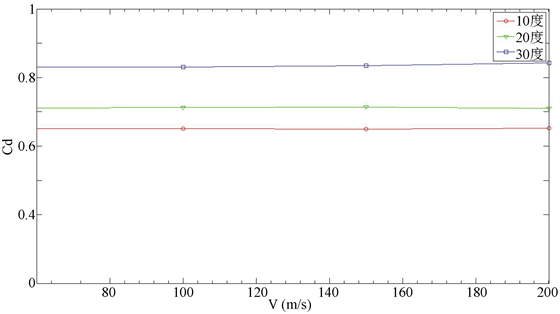
Figure 7. Resistance coefficient-velocity curve of stable parachute
图7. 稳定伞阻力系数–速度关系曲线
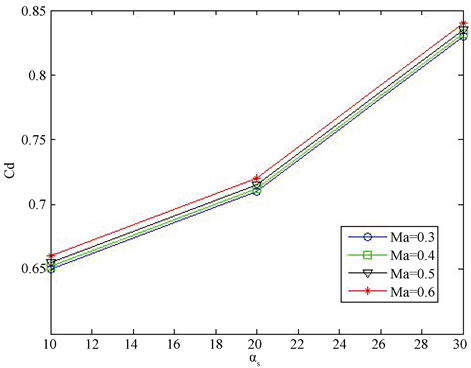
Figure 8. The relationship curve between drag coefficient and brace angle of stabilized parachute
图8. 稳定伞阻力系数–伞撑角关系曲线
5. 总结
本文建立了三种不同伞撑角的稳定伞简化模型,并且采用CFD模拟技术分别把三种模型加入定常、定压的稳定流场下进行气动模拟,然后对模拟结果进行分析得出,稳定伞背风面分离气泡的大小随着伞撑角的改变而改变,进而改变稳定伞的阻力大小,最后得出稳定伞阻力系数与伞撑角的近似解析关系式。在软管–锥套数学模型中,锥套的下沉量由软管–锥套的气动载荷决定,其中锥套所受阻力占主要影响。因此,锥套的阻力大小的改变可以调整锥套的位置,上述关系式适用于软管–锥套系统抑制飘摆运动。