1. 引言
经典判断矩阵主要分为积性判断矩阵 [1] 和模糊判断矩阵 [2] [3] 两类,其元素为单一实数值。由于社会经济环境复杂性或者是某些知识的缺乏,决策者在实际决策过程中通常很难用单一实数值来表达偏好信息。为此,文献 [4] [5] 提出了直觉模糊判断矩阵,其矩阵元素为直觉模糊数 [6] ,能够更好的描述决策者的判断信息。因此,许多学者对直觉模糊判断矩阵进行了充分研究 [7] [8] [9] 。文献 [10] 指出直觉模糊判断矩阵的基础为0.1~0.9标度不符合某些实际决策需要,而1~9标度恰能够补充其不足,进而提出了直觉积性集和直觉积性判断矩阵。文献 [12] [13] [14] 对直觉积性集上的集成算子进行了研究;文献 [15] [16] 研究了基于直觉积性集的层次分析法;文献 [17] 给出了直觉积性判断矩阵的排序区间。我们知道,判断矩阵一致性是判断矩阵理论研究的核心内容,而通常模糊判断矩阵一致性分为加性一致和积性一致性,积性判断矩阵只有积性一致性。
本文在已有模糊判断矩阵积性一致性 [2] [3] 和直觉积性判断矩阵积性一致性 [10] [16] 工作基础上提出直觉积性判断矩阵对数一致性概念,并提出单个和多个直觉积性判断矩阵一致性检验与修正算法,其优点是能够尽可能的保留决策者最初的判断信息,最后通过实例说明算法有效性。
2. 预备知识
本节我们简要介绍直觉积性集和直觉积性判断矩阵相关概念。
定义2.1 [10] :设
为论域集,称
为直觉积性集,其中
表示隶属度,
表示非隶属度,两者满足条件
,
。
为了表示方便,称
为直觉积性数。为了对直觉积性数进行比较,文献 [10] 引入如下方法:
定义2.2 [10] :设
为直觉积性数,称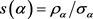 为
的得分函数,
为
的准确函数:
为
的得分函数,
为
的准确函数:
1) 如果
,那么
;
2) 如果
,那么
如果
,那么
;
如果
,那么
。
定义2.3 [11] :对两个直觉积性数
,定义如下距离测度:
定义2.4 [10] :设
为论域集,称矩阵
为直觉积性判断矩阵,其中
为直觉积性数,且满足
。
为了描述决策者给出的双曲直觉积性判断矩阵
间的偏差,我们定义如下距离测度:
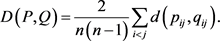
不难发现,偏离测度反映了
偏差的平均值。
3. 直觉积性判断矩阵对数一致性及其检验与修正算法
3.1. 直觉积性判断矩阵对数一致性
本节给出直觉积性判断矩阵对数一致性。首先,我们给出如下引理:
引理3.1:对
,有
1)
;
2)
。
证明:1)由于
,我们有
,
,
所以
;
2)
。
定义3.1:设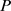 为直觉积性判断矩阵,对所有
如果满足
为直觉积性判断矩阵,对所有
如果满足
,
则称
具有对数一致性。
众所周知,具有一致性的判断矩阵与排序向量之间有密切的关系,我们给出直觉积性排序向量的概念以确定具有对数一致性的直觉积性判断矩阵与直觉积性排序向量之间的联系。
定义3.2:称
为直觉积性排序向量,其中
(
)为直觉积性数。
定理3.2:设
为直觉积性排序向量,则
,其中
且
,
,
,为直觉积性对数一致性判断矩阵。
证明:首先证明
为直觉积性判断矩阵。由于
,由引理3.1不难验证
且
,因此
为直觉积性数。显然
,所以,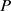 为直觉积性判断矩阵。下证,
为对数一致的,
为直觉积性判断矩阵。下证,
为对数一致的,
所以
为对数一致的。综上,
为直觉积性对数一致性判断矩阵。
3.2. 单个直觉积性判断矩阵对数一致性判断与修正算法
在实际决策中,决策者给出的直觉积性判断矩阵往往不能满足上述对数一致性要求,通常要求其具有可接受的一致性,即,决策者提供的直觉积性判断矩阵与直觉积性对数一致性判断矩阵之间的偏差可接受,否则对其进行修正,使其具有可接受一致性。修正的原则是既要达到一致性要求,又要尽可能的保留决策者最初的判断信息。
定义3.3:设
为直觉积性判断矩阵,
为直觉积性对数一致性判断矩阵,如果对给定阈值
,有
,则称
具有可接受对数一致性。
对给定直觉积性判断矩阵
,我们给出如下检验与修正单个直觉积性判断矩阵对数一致性算法。主要包括如下步骤:
步骤1:建立数学模型
确定排序向量
和相应的直觉积性对数一致性判断矩阵
;
步骤2:计算
,如果
,则具有可接受对数一致性,转向步骤4;否则,不具有可接受对数一致性,从而需要对
进行修正,转下一步;
步骤3:计算
对应位置上元素之间的距离测度
,如果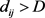 ,则修正
,则修正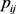 为
,修正后的直觉积性判断矩阵记为
,转向步骤1;
为
,修正后的直觉积性判断矩阵记为
,转向步骤1;
步骤4:由定义2.2计算排序。
容易验证上述算法具有收敛性。
注:上述算法的优点是在对不具有对数一致性的直觉积性判断矩阵进行修正的同时还尽可能的保留决策者最初的判断信息。
例3.1:设决策者提供直觉积性判断矩阵
步骤1:取
,建立数学模型
,可以确定排序向量
和相应的直觉积性对数一致性判断矩阵
;
步骤2:计算
,所以
不具有可接受对数一致性,从而需要对
进行修正,转下一步;
步骤3:计算
对应位置上元素之间的距离测度
,有
,
修正
为
,修正后的直觉积性判断矩阵记为
;
步骤4:建立数学模型
,可以确定排序向量
和相应的直觉积性对数一致性判断矩阵
修正后的直觉积性判断矩阵
步骤5:计算
,所以
具有可接受对数一致性。
步骤6:计算得分
,因此排序为
。
3.3. 多个直觉积性判断矩阵对数一致性检验与修正算法
为了适应群体决策需要,我们给出多个直觉积性判断矩阵的对数一致性检验与修正算法。
定义4.1:设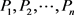 为
个直觉积性判断矩阵,
为具有对数一致性的直觉积性判断矩阵。如果
,则称
相对
具有群体可接受对数一致性。
为
个直觉积性判断矩阵,
为具有对数一致性的直觉积性判断矩阵。如果
,则称
相对
具有群体可接受对数一致性。
我们提供如下算法来实现多个直觉进行判断矩阵对数一致性的检验与修正:
步骤1:建立数学模型
确定排序向量
和直觉积性对数一致性判断矩阵
,如果
,则转到步骤4;否则,不满足群体对数一致性,需要对
中某些矩阵进行修正,转到下一步;
步骤2:记
,挑选直觉积性判断矩阵
使得
;
步骤3:计算
相应位置上元素
之间的距离
,如果
,则将修正
中的元素
为
,相应直觉积性判断矩阵记为
,转向步骤1;
步骤4:计算直觉积性对数一致性判断矩阵
排序向量
的得分值,进行排序。
与单个直觉积性判断矩阵对数一致性检验与修正算法类似,这里多个直觉积性判断矩阵对数一致性检验与修正算法也具有收敛性。
注:上述算法优点在于能够在修正对数一致性的同时,尽可能的保留了决策者最初的判断信息。
例3.2:设在一群体决策过程中三位专家给出的直觉积性判断矩阵
如下:
。
通过以下步骤对
的对数一致性进行检验与修正:
步骤1:建立数学模型
确定排序向量
和直觉积性对数一致性判断矩阵
,我们有
,
,
;
步骤2:计算
,
,因此需对
进行修正;
步骤3:计算
对应位置上元素之间的距离测度
,有
,
修正
为
,修正后的直觉积性判断矩阵记为
;
步骤4:建立数学模型
确定排序向量
和直觉积性对数一致性判断矩阵
,我们有
,
修正后的直觉积性判断矩阵
,
,
;
步骤5:计算
,
,因此需对
进行修正;
步骤6:计算
对应位置上元素之间的距离测度
,有
,
修正
为
,修正后的直觉积性判断矩阵记为
;
步骤7:建立数学模型
确定排序向量
和直觉积性对数一致性判断矩阵
,我们有
,
,
,
所以,修正后的直觉积性判断矩阵
具有可接受对数一致性。
步骤8:计算得分
,因此排序为
。
4. 小结
本文在已有判断矩阵及其一致性工作基础上引入了直觉积性判断矩阵对数一致性,并给出了能够尽可能保留决策者判断信息的一致性检验与修正算法,通过例子说明了算法的有效性。
共识性是基于判断矩阵群体决策的另一重要研究内容,作为本文的进一步研究,我们将给出能够同时兼顾直觉积性判断矩阵共识性和一致性的新算法。
基金项目
临沂大学大学生创新创业训练项目(No. 201710452004);山东省自然科学基金(No. ZR2017MG027)。