1. 引言
电子商务是一种基于互联网平台的买卖双方直接在网上进行交易的商业模式。近些年电子商务的迅猛发展为消费者提供了购物的便利,造就了淘宝天猫,京东商城等电子商务巨头。文献 [1] 指出电子商务造就了一个复杂的生态系统,衍生出了大量的产业,许多公司集聚而来。不仅如此,文献 [2] 中介绍了电子商务成为中国经济转型的重要风口,是战略性新兴产业,对国家发展的重要性不言而喻。但是经过了这么多年的发展,电商交易规模急剧增长的情况下是否已经趋于饱和,是否还有更强劲的动力等都是问题,文献 [3] [4] 对电子商务的现状与未来做了一些报道;但是基于数理模型研究论文极少。文献 [5] 通过灰色模型利用四年的年数据来预测未来跨境电商规模,文中仅用几个点进行趋势预测,显然时间越长偏差会越明显。所以建立一个比较有效的预测模型,无论对消费者,电商巨头,行业研究,还是国家未来的经济发展以及就业预计都将提供帮助。
模型方面,文献 [6] 提出了随机logistic人口增长模型,运用了低阶累积量函数的微分方程。文献 [7] [8] 也是利用logistic模型对人口增长进行应用预测和研究。文献 [9] 提出基于李雅普诺夫指数的状态反馈控制策略,消除混沌logistic增长模型中的混沌轨道,并给出控制条件。本文从数学角度选择三个模型对电子商务规模数据进行探讨分析并作出推断,研究方法与结果具有一定的理论价值和实际意义。
2. 模型介绍
2.1. 二次函数增长模型
模型假设电子商务交易金额增长率是常数,即单位时间内电子商务交易金额的增长量与当时的电子商务交易金额成正比。定义
为t时刻的电子商务交易金额,可以得到
2.2. 指数函数增长模型
模型假设今年电子商务交易额
,年增长率r,k年后电子交易额为
。
且电子商务增长率r是常数(或单位时间内电子商务的增长量与当年的电子商务交易额成正比)。
为t时刻的电子商务交易额;模型的表达式为
。
2.3. 阻滞增长模型
根据前两个模型可以得到电子商务交易量数据的无穷增长的结论,显然这有一定的不合理。而阻滞增长(logistic)模型考虑到了自然资源、环境条件等因素对电子商务交易金额的增长起着阻滞作用,并且随着电子商务交易金额的增加,阻滞作用会越来越大。所以有如下模型:
这里参数r是该模型的内禀增长率,
是自然资源和环境条件所能容纳的最大电子商务交易金额数据。当x =
时,电子商务交易金额不再增长,即此时增长率为0。对上述方程求解可以得到
。
3. 实证检验
3.1. 模型的描述统计
我们选取艾瑞网上摘录的2010年第一季度到2016年第四季度的电子商务交易数据(见表1)共计28个进行实证分析。

Table 1. E-commerce transaction data in quarter from 2010 to 2016
表1. 电子商务2010年~2016年季度交易规模数据(万亿)
利用二次模型,指数模型和阻滞增长模型对上述数据的分析结果进行简单的汇总比较,相关的模型统计量描述和方差分析结果如表2所示:

Table 2. Statistical description of models
表2. 模型的统计描述
从表2可以看出,三个模型的拟合度(R2值)均达到了0.9以上,而方差分析的Signif F值均明显小于0.01,因此这三个模型的拟合结果均具有统计上的意义。
三个模型的判定系数均接近于1,所反映的自变量与因变量的相关性较高,模型的拟合程度较好。虽然三个模型的拟合程度均不相上下,但是我们可以明显的发现逻辑曲线和指数曲线的标准误差项明显较小,我们可以初步认为其更适用于电子商务规模的增长模型。
3.2. 三个模型的拟合结果描述
本文用数学软件对这三个模型曲线进行拟合,相关参数数据描述如下。
二次模型:因变量y对自变量时间t,t2的非标准化回归系数分别为0.023,0.005,对应的显著性检验的T值分别为0.949,5.808;显著性水平方面,变量t的sig > 0.05,显著性水平不强;而t的平方项的sig < 0.05,显著性水平较强。对应的二次曲线模型为:
指数模型:因变量ln(y)对自变量时间t的非标准化回归系数为0.060,对应的显著性检验的T值为39.954,回归系数的显著性水平sig T值小于0.05。
对应的指数回归方程为:
阻滞模型:因变量
对时间t的非标准化回归系数为0.936,对应的显著性检验的T值为592.701,回归系数的显著性水平sig T值小于0.05。
对应的logistic模型的回归方程是:
3.3. 三条曲线的拟合曲线及预测图
上面的三张图是通过对三个模型进行拟合得到的实际效果图(见图1),可以看出对于已有的数据的拟合效果还算不错。但是第1张和第2张往后将呈现爆炸性的增长趋势显然不符合实际,第3张就比较合理的预计再经过十年左右电子商务规模将渐趋于一个上限。
4. 模型的残差分析
4.1. 自相关分析检验残差的独立性
图2是对三个模型的残差项用R软件所做的自相关函数图(ACF)。
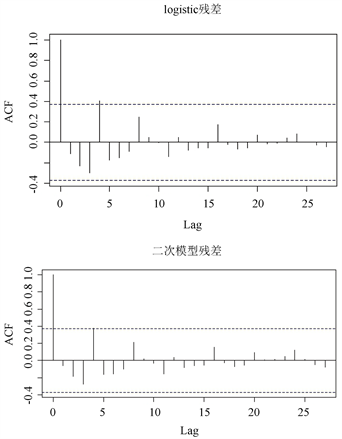
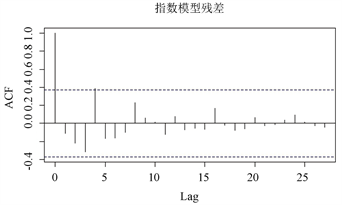
Figure 2. Residual autocorrelation coefficient
图2. 残差自相关系数
从上面三个残差的自相关系数图可以看出,样本长度为28,自相关系数服从以0为均值,
为标准差的正态分布,当自相关系数落在以区间(−
,
)为独立置信区间时,我们就认为误差项是均值为
0的独立同分布随机变量序列。从图中我们可以得出残差项存在独立性。
4.2. 残差的正态分布检验
图3分别是二次,指数,阻滞模型的残差的直方图。
可以看出残差项近似的服从正态分布,均值为零。由于电子商务正处于初始的加速上升阶段所以拟合效果均不错差异性不是很大。
4.3. 未来季度数据预测

Table 3. Quarterly Data Forecast in the future
表3. 未来季度数据预测(万亿)
5. 结束语
在模型的拟合结果中我们可以看出,二次曲线和指数曲线模型拟合值与前期数据比较吻合,这说明目前我国的电子商务正处于迅猛发展时期,但考虑到环境因素等原因,未来不可能一直持续这一趋势。当资源有限时,电子商务交易总额的增长率将会随着基数的增大而减小,由此我们认为电子商务交易额的增长速度会缓慢下降,即随着电商交易额的增加而降低,存在着增长有限性的特征。阻滞增长模型,更能描述电子商务的发展趋势,对数据进行拟合,结果可以看出阻滞增长模型拟合得到的数据客观的反映了电子商务增长规律,与现有数据非常吻合,并且对未来电商交易金额的预计(见表3)也在我们的理想范围之内,效果更为准确。
根据模型的拟合效果预测图也可以看出未来十年电商交易规模仍旧会有着较强的发展势头,并将在未来五年内突破年交易量五十万亿大关。伴随着大量传统企业的转型升级和智能物流体系的建立,电子商务的交易金额将牵动着国民生产总值的发展,电商的地位将日益抬高,政府对电商的支持度也是日益增加,这表明电商在中国经济市场未来将占有相当大的份额,未来将是中国经济强劲增长的非常重要的一环。我们不仅要看到电商以前辉煌的成就,也要瞄准电商充满机遇的未来。
基金项目
国家社科基金17BTJ023资助。