基于虚拟正交试验的关节轴承挤压成形数值模拟分析

Numerical Simulation Analysis for Spherical Plain Bearing Extrusion Based on Virtual Orthogonal Experiment

摘要: 以国产某型号关节轴承为研究对象，基于自开发有限元平台建立关节轴承挤压装配过程的有限元仿真模型。基于模拟仿真的虚拟正交试验，选取轴承内外圈间隙，模具挤压行程等工艺参数作为实验因素，选取轴承密合度为衡量目标，通过正交试验设计，对多目标工艺参数进行优化，并得到了不同工艺参数对轴承密合度的影响程度以及较优的工艺参数。

Abstract: Based on the self-developing platform, the finite element simulation model of the extrusion as-sembly process for a certain type of domestic joint bearing was established. Based on the simulation of the virtual orthogonal experiment, the bearing inner and outer ring clearance and die extrusion stroke process parameters were selected as the experimental factors. Selecting bearing fit as the measuring goal, through the orthogonal experiment design, the multi-objective process parameters were optimized, the influence degree of different process parameters on bearing fit was known, and the optimum process parameters were obtained.

1. 引言

关节轴承因其具有承载能力大，抗冲击性强、润滑好等优点，广泛应用于航空、航天、风电、动车、重载铁路货车等高新技术企业。关节轴承的结构主要包括：内圈，外圈，衬垫。其成型过程，通常是利用冷挤压的方法，将外圈内表面沿着内圈外表面挤压成型。作为关节轴承一种重要的成型方法，冷挤压具有高效、优质、低耗等特点 [1] [2] [3] 。

目前已有学者运用有限元方法对轴承挤压过程进行了研究。吴连平等提出了一种集数值仿真，人工神经网络和遗传算法为一体的关节轴承模具型腔优化设计方法，合理的设置了模具参数，有效提高了轴承内外圈间隙的均匀性 [4] 。陈清伟针对目前仿真与试验存在较大误差的问题，通过修正仿真模型中的衬垫参数，有效提高了仿真模型精度 [5] 。杨庆华等提出了一种结合正交实验法，BP神经网络和遗传算法的模具优化设计方法，试验结果表明，最大行程载荷与凹模磨损量，优化结果与仿真结果相接近，提出的方法有效的降低了模具设计周期 [6] 。

但由于关节轴承在批量加工过程中内外圈间隙不同，同时关节轴承在挤压过程中，随着模具挤压行程不同，关节轴承密合度皆不相同，上述文献对挤压进行仿真时，忽略了上述两因素对轴承密合度的影响。基于此本文基于虚拟正交试验，对上述两因素进行实验分析。

2. 有限元模型的建立

本文选用某型号自润滑关节轴承进行仿真计算，挤压前的外圈及内圈尺寸如图1、图2所示。外圈材料05Cr17Ni4Cu4Nb，内圈材料G95Cr18，衬垫材料为PTFE混合编织物。依据关节轴承尺寸图纸，设计模具图纸如图3所示。根据模具和轴承实际尺寸完成每个零件的几何模型，并按实际工况进行装配。由于挤压过程轴承几何形状和受力都是对称的，现取整个挤压模型的1/2进行模拟计算。轴承合套挤压模型由内圈、衬垫、外圈、上模具、下模具组成，所建立的有限元模型如图4所示。

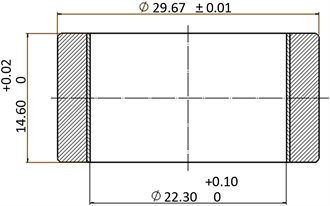
Figure 1. The outer ring of the spherical plain bearing

图1. 关节轴承外圈

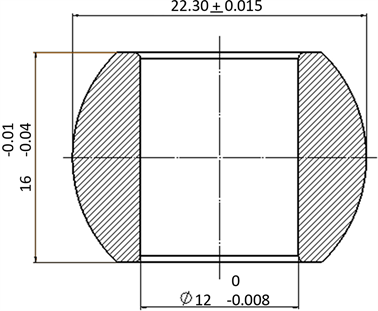
Figure 2. The inner ring of the spherical plain bearing

图2. 关节轴承内圈

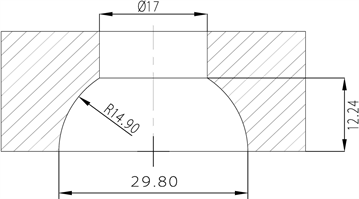
Figure 3. The extrusion mold of the spherical plain bearing

图3. 关节轴承挤压模具

由于关节轴承挤压装配过程属于材料非线性，几何非线性，接触非线性的问题，采用自开发求解器进行求解。根据实际运动关系，本文定义三个接触对。接触面之间的摩擦采用库伦摩擦定律，内圈与衬垫之间动摩擦因数取为0.6，最大静摩擦因数取为0.1，外圈与上、下模具的动摩擦因数取为0.1，最大静摩擦因数取为0.12，衬垫粘贴于外圈内表面。轴承沿Z方向进行位移固定约束，上模具和下模具，沿Y方向进给运动，上下模具采用解析刚体进行求解，每个刚体设置一个参考点，用参考点代表其运动。由于轴承为对称模型采用扫掠方式进行网格划分，模具采用自由网格进行划分。为避免沙漏模式产生，对模型全局进行均布网格划分。为在较短的计算时间内得到高质量的计算结果，本文将模型各部件密度放大100倍。

3. 虚拟正交试验方案的确立

虚拟正交试验设计也称正交设计，是试验设计的基本工具，它是根据均衡分布的思想，运用组合数学理论构造的一种数学表格，具有很强的实用性 [7] [8] 。

在关节轴承样件加工过程中，内圈外径尺寸通过磨床进行最后一道工序加工，因而具有较高的尺寸精度，外圈内表面通过喷砂方式进行最后一道工序，然后以涂胶方式将衬垫粘贴于其内表面，因而导致外圈尺寸精度较低，对于批次产品而言，易产生不同间隙，如图5所示。间隙值的大小由公式(2-1)和公式(2-2)所示。

Figure 4. The combined extrusion finite element model of the spherical plain bearing

图4. 关节轴承合套挤压有限元模型

$\Delta t=粘贴衬垫后外圈内径-内圈外径$ (2-1)

$间隙值=2\times \Delta t$ (2-2)

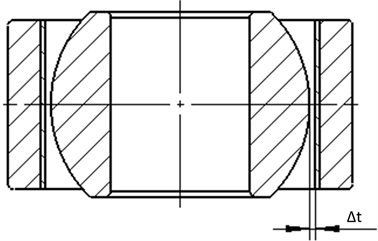
Figure 5. The schematic diagram bearing for the clearance of the inner ring and outer ring

图5. 内外圈间隙示意图

图6为该型号关节轴承在间隙值为0时，从模具开始接触关节轴承挤压开始到挤压结束，关节轴承密合度随挤压行程变化趋势图，横坐标对应挤压行程，纵坐标对应轴承密合度。由图可知，初始阶段上下模具开始接触轴承外圈，外圈变形较小，密合度值较大，同时变化较小。随着上、下模合模过程的进行，外圈变形逐渐增大，开始出现密合度小于标准值0.07的区域，并在某一时刻达到最小值。随着模具继续合模，外圈端面位置变形较轴承中间位置变化更加明显，密合度值逐渐增大，随着挤压过程的结束，轴承密合度达到某一固定值。

根据上述所选的工艺参数结合正交试验，设置两个因素，内外圈间隙d及挤压行程c。间隙值的确定，以内外圈最大间隙0.12作为上限，对区间内的间隙值进行等差划分。挤压行程的确定为对密合度符合标准的行程区间进行取值，得到因素水平表如表1所示。

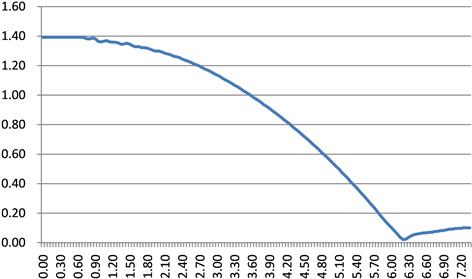
Figure 6. The schematic diagram bearing for the clearance of the inner ring and outer ring

图6. 关节轴承密合度随时间变化趋势图

Table 1. The horizontal elements of figure orthogonal experiment

表1. 正交试验水平要素图

4. 仿真结果分析

由于轴承密合度是自润滑关节轴承最重要的性能指标之一，用于考核其成形加工后内外圈间隙的均匀性，是保证轴承寿命和运行平稳性的关键因素，本文选取密合度作为正交试验衡量指标。文中分别建立间隙值为0至0.12的有限元模型，选取密合度符合标准的区间范围的挤压行程。根据此因素水平表，建立两因素，四水平正交试验表，得到16组试验方案，并对每组方案进行有限元分析，分析结果如表2所示，其中δ代表轴承密合度、r代表极差。

Table 2. The table of the virtual orthogonal experiment

表2. 虚拟正交试验表

通过虚拟正交试验，可获得各因素对各指标的极差值，进而获得各优化指标影响因素的主次顺序，由极差r可知，综合考虑挤压行程及轴承内外圈间隙两因素，影响密合度的主次顺序为：挤压行程d > 轴承间隙c。同时考虑轴承密合度在实际使用过程中越小越好，实验方案中选取d 1，c 4作为批次产品生产的工艺参数。

5. 结论

基于正交试验，对自润滑关节轴承挤压成形过程进行了数值模拟分析，确定了关节轴承在密合度δ ≤ 0.07时的影响因素为：挤压行程 > 轴承间隙，同时在批次产品生产过程中，确定了相对较优的工艺参数。

基金项目

国家国际科技合作专项2015DFR50750。