1. 引言
魔方又叫鲁比克方块,于1974年匈牙利布达佩斯建筑学院鲁比克教授发明。它是一个由26个小方块连结在一起组成的大立方体 [1] 。小方块分为3类:6个中心块(只有一个颜色面,决定了魔方表面的颜色)、8个角块(3个颜色面)和12个边缘块(2个颜色面),中心块绕着本身旋转,角块和边缘块绕着中心块旋转。魔方有6种水平方向转动( )、6种垂直方向转动(
)、6种垂直方向转动( )、前表面有顺时针和逆时针2种转动(
)、前表面有顺时针和逆时针2种转动( ) [2] 。小方块有3种状态:归位、定向、复原。归位是指小方块的位置不正确,需翻转到合适位置;定向是指小方块位置已正确,但其各表面颜色指向不对;复原是指小方块的位置及其各表面颜色指向都正确。
) [2] 。小方块有3种状态:归位、定向、复原。归位是指小方块的位置不正确,需翻转到合适位置;定向是指小方块位置已正确,但其各表面颜色指向不对;复原是指小方块的位置及其各表面颜色指向都正确。
魔方手动求解方法很多,分层方法、棱方法、桥式方法、角方法、CFOOP方法、CFOP方法、笑面虎方法等。其中,CFOP方法是世界上使用最广泛的快速复原魔方方法。此方法使用了119个公式,分4个步骤复原魔方 [3] 。计算机求解魔方,就是用编程方法,让计算机复原任意一种打乱状态的魔方。计算机求解魔方有两种方法:穷举法和层次法。穷举搜索法 [4] 需要解决三个难题:如何用公式描述魔方状态、魔方状态的存储、魔方状态和魔方的操作对应。由于魔方状态千变万化,穷举搜索法求解效率极低。
本文分析计算机求解魔方的经典算法:层次法。该复原方法 [5] 包含七个步骤:第一步,形成上层十字,任选一面,归位四个角块的位置和颜色;第二步,把上层四个边缘块的位置和颜色归位;第三步,归位中层四个边缘块的位置和颜色;第四步,下层形成十字,把下层四个角块的位置归位;第五步,归位下层四个角块的颜色;第六步,把下层四个边缘块的位置归位;第七步,把下层四个边缘块的颜色归位。本文设计实现了这七个步骤的算法流程,并用图例详细解释每一步复原过程。
2. 建立数学模型
首先建立图1所示的三维坐标:每个小方块用其右前上角的坐标表示,小方块的面颜色用垂直于该面的坐标轴表示,即每个小方块用四元组表示,如图1上表面为蓝色的角块,表示为(3, 3, 3, z)。魔方的前后左右上下各个面分别用front、behind、left、right、upper、bottom表示。一连串拧转魔方的操作是通过若干次(upper或bottom面)水平方向左右转动90度、(left或right面)垂直方向上下转动90度、front面顺时针或逆时针转动90度实现。如串操作 表示,魔方front面首先顺时针转动90度、bottom面水平向右转动90度、front面逆时针转动90度、right面垂直向上转动90度这四个动作。
表示,魔方front面首先顺时针转动90度、bottom面水平向右转动90度、front面逆时针转动90度、right面垂直向上转动90度这四个动作。
3. 求解算法框图设计
完整求解算法框架如下所示:
Input:待复原的魔方
Output:已复原的魔方
1 Stage 1:上层小方块复原
2 上层角块复原,算法1流程
3 上层边缘块复原,算法2流程
4 Stage 2:中层小方块复原
5 中层边缘块复原,算法3流程
6 Stage 3:下层小方块复原
7 下层角块归位,算法4流程
8 下层角块定向,算法5流程
9 下层边缘块归位,算法6流程
10 下层边缘块定向,算法7流程
11 Result:魔方复原
3.1. 魔方上层复原
魔方上层复原就是使这一层所有小方块的上表面颜色与中心块颜色一致,同时,同一侧面的各个小方块颜色也要一致。魔方初始状态如图1所示,魔方整体向左旋转90度,之后寻找和角块(3, 1, 3)一样的目标角块(3个颜色面,一面为蓝色,一面为(3, 1, 3, x)的颜色),使角块目标处于图2(a)标示的位置(黑色编号所示位置),执行算法1 (图3所示)流程,上层角块复原(图2(b)所示)。在本文所示的算法流程图中,例如图3,Switch (3, 1, 3, x)表示位于x轴上3位置、y轴上1位置、z轴上3位置的小方格,面的颜色为垂直于x轴的面颜色;Case (3, 3, 1, y)表示位于x轴上3位置、y轴上3位置、z轴上1位置的小方格,面的颜色为垂直于y轴的面颜色。算法1中 分支表示若图2(a)中所示的编号①标记的方块,且面颜色为y轴指向的面颜色(红色)与Switch (3, 1, 3, x)指向的面颜色一致,就执行系列拧转操作(
分支表示若图2(a)中所示的编号①标记的方块,且面颜色为y轴指向的面颜色(红色)与Switch (3, 1, 3, x)指向的面颜色一致,就执行系列拧转操作( ),则(3, 3, 3)角块复原。魔方整体向右再次旋转90度,若此时转到(3, 3, 3)位置的角块已复原,则上层角块复原完毕。
),则(3, 3, 3)角块复原。魔方整体向右再次旋转90度,若此时转到(3, 3, 3)位置的角块已复原,则上层角块复原完毕。

Figure 1. The coordinates of the cubes
图1. 魔方各个小方块的坐标
 (a)
(a)  (b)
(b) 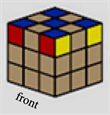 (c)
(c)  (d)
(d)
Figure 2. Initial and target states of upper layer. (a) Initial state of module 1, (b) Target state of module 1, (c) Initial state of module 2, (d) Target state of module 2
图2. 上层复原状态图及目标图。(a) 算法1状态图,(b) 算法1目标图,(c) 算法2状态图,(d) 算法2目标图
寻找目标边缘块(两个颜色面,一面为蓝色,一面为(3, 1, 3, x)的颜色),旋转中层及底层,使目标边缘块位于图2(c)标示出的位置(黑色编号所示位置),执行算法2 (图4所示)流程,上层边缘块复原,结果如图2(d)所示。
3.2. 魔方中层复原
在算法2目标图(图3(d)所示)基础上,旋转魔方中层,使中层中间方块颜色(3, 2, 2, x)与顶层方块侧面颜色(3, 2, 3, x)一致;旋转魔方下层,得到图5(a)状态,执行算法3 (图6所示)流程,将中层边缘块复原(图5(b)所示)。
 (a)
(a)  (b)
(b)
Figure 5. Initial and target states of middle layer. (a) Initial state of module 3, (b) Target state of module 3
图5. 中层复原状态图及目标图。(a) 算法3状态图,(b) 算法3目标图
3.3. 魔方下层复原
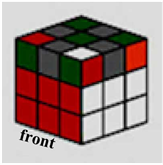
第一步复原四个角块,第二步复原四个边缘块。将算法3的目标图翻转,下层翻转到上层,蓝色面翻到底面,白色面翻到左侧,利用算法4 (图7所示)流程归位四个角块。该流程将图8(a)中②或③编号位置上为红绿白三色的角块转到①编号位置,即(3, 3, 3)位置。
 (a)
(a)  (b)
(b)
Figure 8. Initial and target states of corner cubes of bottom layer. (a) Initial state of module 4, (b) Target state of module 4
图8. 下层角块归位状态图及目标图。(a) 算法4状态图,(b) 算法4目标图
角块归位后,还需定向操作。无论这四个角块是否出现图9(a)所示的三种情况,都执行算法5 (图10所示)流程。执行算法5流程时,需要轮流操作9(a)所示的三种情况,直至四个角块全部复原(见图9(b)所示),算法5结束。
 (a)
(a) (b)
(b)
Figure 9. Initial and target states of corner cubes of bottom layer. (a) Initial state of module 5, (b) Target state of module 5
图9. 下层角块定向状态图及目标图。(a) 算法5状态图,(b) 算法5目标图
魔方下层复原的第二步:复原四个边缘块。若算法5执行完毕,目标图中没有如图11所示的归位边缘块,先执行一次算法6 (图12所示),之后将归位的边缘块所在的面转到前面;然后继续执行算法6流程,直到四个边缘块全部归位。
 (a)
(a) 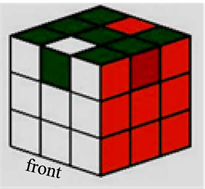 (b)
(b)
Figure 11. Initial and target states of edge cubes of bottom layer. (a) Initial state of module 6, (b) Target state of module 6
图11. 下层边缘块归位状态及目标图。(a) 算法6状态图,(b) 算法6目标图
下面完成四个边缘块定向。算法6流程结束时,至少有两个边缘块定向,结果会出现图13所示的两种情况。执行算法7 (图14所示)流程,将剩下的两个边缘块定向,至此,魔方复原成功。

Figure 13. Initial state of edge cubes of bottom layer
图13. 算法7初始状态
4. 结束语
魔方设计更好地理解了三维空间的各种运动。对于计算机求解,要求具有一定的智能判断能力;在对魔方状态进行判断后,根据算法设定,匹配最佳操作。本文研究的对象是三阶魔方,图例结果说明,本文算法适用于打乱状态的三阶魔方,算法设计是可行的。文献 [6] 利用android手机中的DroidCam软件和LabVIEW软件实现魔方复原。文献 [7] 从分析的角度给出了基于Arduino电子平台的一种魔方复原方案。而本文的研究工作旨在Visual studio 2010开发环境下编程实现三阶魔方复原,并结合OpenGL提供的强大三维绘图功能,开发一款3D虚拟魔方软件,处理Windows输入消息,通过操作键盘复原魔方。
致谢
衷心的感谢郝航行同学,他的学士学位论文《基于OpenGL的魔方游戏的设计与实现》中的图片,对阐明本文算法流程图帮助很大。