水文模型在山洪模拟中的比较应用

Comparison and Application of Hydrological Models in Mountain Flood Simulation

摘要: 山洪灾害频繁发生，给社会造成了重大经济损失，因此水文模拟对山洪灾害防治具有重要现实意义。为研究不同水文模型在山洪预报中的模拟效果，以官山河流域为例，使用新安江模型、TOPMODEL模型和改进的SCS模型等三种模型对多场场次洪水进行模拟研究。使用1973~1987年的逐日逐时降雨径流资料对模型参数率定，取其中15场典型洪水进行模型验证。从三种模型模拟效果来看，模拟效果一般。TOPMODEL模型对洪峰流量拟合得较好，平均相对误差为23.14%，合格率为40%；改进的SCS模型与TOPMODEL模型对峰现时间模拟较好，合格率均为93%；改进的SCS模型对洪量模拟效果最佳，相对误差为20.73%，合格率为67%。TOPMODEL半分布式水文模型能从物理层面更为真实地描述自然界的洪峰流量响应过程，改进的SCS模型提高了地下径流的贡献而使得洪量模拟效果相对较好。

Abstract: Mountain flood disasters occur frequently, causing major economic losses to society. Therefore, hydrological simulation has important practical significance for the prevention and control of mountain flood disasters. In order to study the simulation consequence of different hydrological models in mountain flood forecasting, taking the Guanshan river basin as an example, Xin’anjiang model, TOPMODEL model and improved SCS model were used to simulate multi-field floods. The model parameters were determined using the time by day rainfall runoff data from 1973 to 1987, and 15 typical floods were used for model verification. From the simulation results of the three models, the simulation effects are general. The TOPMODEL model fitted the peak flow better. The average relative error is 23.14%, and the pass rate is 40%. The improved SCS model and the TOPMODEL model have better peak-to-peak time simulation, and the pass rate is 93%; the improved SCS model’s simulation effect on the flood amount is the best, the relative error is 20.73%, and the pass rate is 67%. The TOPMODEL semi-distributed hydrological model can describe the flood peak flow response process in the natural world from the physical level more realistically. The improved SCS model improves the contribution of underground runoff and makes the flood simulation effect relatively better.

1. 引言

山洪灾害是由突发性暴雨造成的山区洪水灾害，具有短历时、高强度特点。我国山区面积占全国土地面积69%，且山洪灾害频发。我国有超过一半的人口分布在山区，山洪灾害给国民经济带来的损失严重 [1] 。

大约40年前就开始有研究者在降雨及山洪方面进行研究 [2] ，国外开展的山洪预警预报研究比我国开展得要早。如以美国为代表的发达国家，已经构建较为成熟的山洪预警预报系统如山洪预警指南系统(FFG)，基于水文模型的动态临界雨量法已广泛使用，而我国刚初步采用临界雨量的计算方法，正在推广使用分布式水文模型和动态临界雨量法 [3] 。在山区流域洪水预报实际工作中，在国外，Gunter Bloschl等在奥地利北部山区应用分布式水文模型模拟山洪过程，使得模拟精度提高10%~30% [4] ，Isabelle Braud等应用分布式水文模型模拟法国东南部流域2002年山洪过程，模拟效果也较好 [5] 。

国内沿用传统大江大河建模思路从淹没角度建立了以经验归纳统计法和水文水力学方法为手段的洪水预报模型，初步提出了“一维简化水动力学模型”、“分布式水文模型”和“多维完整水动力学模型”等模型。如王璐等将5种常用的水文模型应用于湿润、半干旱半湿润地区的14个典型山区小流域，在山区开展模型适用性研究，得出在湿润地区，API、新安江、TOPMODEL模型模拟效果较好而不管在湿润地区还是半湿润半干旱地区，HEC-HMS模型适用性最强的结论 [6] ；包红军将基于新安江模型建立的分布式混合产流GMKHM水文模型和分布式新安江模型应用于2009年汛期嘉陵江乔庄河支流大沟小流域山洪预报试验，得出两个分布式模型均适用于所研究小流域 [7] ；刘志雨等以动态临界雨量为指标，在江西遂川江流域应用了GBHM分布式水文模型 [8] ；郭良等提出构建以分布式水文模型为基础的山洪预警系统建设思路 [9] ；潘佳佳等比较了暴雨山洪动力学、运动波模型、扩散波模型的应用效果等等 [10] 。

但是我国山区环境复杂，山洪灾害突发性和局地性强，对山区暴雨洪水形成时空特征、致灾机理认识不够深入，监测预报预警的准确性和及时性不高，与国外发达国家普遍采用的实时动态预警方式相比，存在较大差距 [11] 。国家科技部“重大自然灾害监测预警与防范”重点专项2017年度项目申报指南中明确提出，山洪洪峰流量预报精度要由40%提高到50%，说明了我国山洪预报精度依旧普遍偏低的现状。针对目前我国山洪灾害突发性和区域性强、山洪灾害预警技术还未成型，预警系统尚未建立完善等现状，充分利用历史山洪灾害资料和实验资料，开展山区暴雨洪水时空演变特征、山洪灾害发生预警阈值、山洪形成机理和致灾机制、山洪模拟预报等基础性研究成为迫切需求 [12] 。

无资料小流域洪水模拟是山洪灾害预警预报的基础，本文旨在通过选取几种不同的典型水文模型模拟研究区暴雨洪水过程，对比分析不同模型模拟结果，总结不同模型适用条件，学习各个模型在机理分析中的建模思路，对研究区洪水预报做出初步尝试，以期后续构建适用于研究区的水文模型，提高山洪预警预报精度，减少山洪灾害造成的损失。

2. 模型概述

2.1. TOPMODEL模型

TOPMODEL模型是一个基于地形的有一定物理机制的半分布式水文模型，其利用地形指数 $\ln \left(a/\tan \beta \right)$ 或地形-土壤指数 $\ln \left(a/T\tan \beta \right)$ (a = 单位等高线长度的排水面积、 $\tan \beta$ = 地表坡度、T = 导水系数)来反映流域水文现象特别是径流运动的分布规律 [13] 。

TOPMODEL模型在流域中将任意一点沿垂向可分为三层：分别是植被根系层(S_rz)、土壤非饱和层(S_uz)、饱和地下水区，用饱和地下水面到流域土壤表面的距离z_i表示。将研究流域划分成若干单元网格，降雨首先按一定速率下渗进入植被根系层，补给该层土壤缺水量，该层水分会有部分蒸发，满足该层土壤贮藏容量和蒸发消耗后的水量能够进一步下渗进入非饱和层土壤。在非饱和层中，水份按一定重力排水速率Q_v下渗进入饱和地下水层，接着经由侧向流动形成基流Q_b。随着饱和地下水位逐渐抬高，在流域的下游河道等处便有水分冒出，形成饱和坡面流Q_s。流域总径流Q就是由基流和饱和坡面流组成，即 $$ [13] [14] 。

2.2. 新安江模型

新安江模型是在我国南方湿润地区有着广泛应用的集总式模型。模型的核心是流域蓄水容量曲线 [15] ，新安江模型首先对蓄满单元流域进行产汇流计算，得出单元流域的出口流量过程，再进行出口以下的河道洪水演算，把各个单元流域的出流过程叠加，求得流域的总出流过程 [16] 。蒸散发计算采用三层蒸散发模型；产流计算采用蓄满产流模型；用自由水蓄水库结构将总径流划分为地表径流、壤中流和地下径流3种；地表汇流计算采用单位线法；壤中流和地下径流汇流计算采用线性水库法。

2.3. 改进的SCS模型

SCS模型是美国农业部水土保持局(Soil Conservation Service, SCS)于1958年研发并应用于小流域的设计洪水模型，Mishra等提出的改进的SCS模型的产流机制为超渗产流机制，并假设下渗速率fc和接近无穷大时的最小渗透速率相等 [17] [18] [19] 。改进的SCS模型根据水量平衡原理及比例相等假设计算地面径流，降雨扣掉初损后下渗的部分分为下渗的静态部分(Fc)和动态部分(Fd)，动态下渗部分补充土壤含水量，静态下渗部分渗透到地下水位，最终在流域出口流出。不管土壤毛细管含水量是否得到满足，静态下渗部分(Fc)都会形成地下径流。本文地表产流汇流采用瞬时单位线法，地下径流汇流采用线性水库法，流域出口断面总径流包括地表径流和地下径流，即总径流 $Q=Q_s+Q_g$ 。

2.4. 模拟误差评定标准

1) 洪峰流量相对误差

$Q_e=\frac{\left|Q_{p,sim}-Q_{p,obs}\right|}{Q_{p,obs}}\times 100\%$ (1)

式中： $Q_{p,sim}$ 、 $Q_{p,obs}$ 分别为场次洪峰流量的模拟值与实测值，m³/s；Q_e为场次洪峰流量相对误差，%，所有场次取其平均值即为流域洪峰流量平均相对误差，取实测洪峰流量的±20%作为许可误差。

2) 峰现时间误差

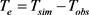(2)

式中：T_sim、T_obs分别为峰现时间的模拟值与实测值；T_e为峰现时间误差，h，3 h内视为合格。

3) 洪量相对误差

$V_e=\frac{\left|V_{sim}-V_{obs}\right|}{V_{obs}}\times 100\%$ (3)

式中：V_sim、V_obs分别为场次洪水流量的模拟值与实测值，m³/s；V_e为场次洪水流量相对误差，%，所有场次取其平均值即为流域洪水流量平均相对误差，以实测值的±20%作为许可误差。

4) 合格率

$QR=\frac{n}{m}\times 100\%$ (4)

式中：QR为合格率；n为合格模拟次数；m为模拟的总次数。

3. 模型应用与结果分析

3.1. 研究区概况

本文以官山河流域作为研究区，官山河流域位于湖北省汉江中上游、丹江口市西南部，地处东经110˚48'~111˚34'59''，北纬32˚13'16''~32˚58'20'' (如图1)，总人口为14,619人，户数为3854户，人口密度为241人/km²。流域面积465 km²，孤山水文站控制流域面积为322 km²，河道平均坡降5.7‰，多年平均流量7.78 m³/s。流域地形以中小起伏山地、丘陵为主，海拔为240~1606 m，平均高程690 m，大部分地区坡度在15˚~25˚，流域地势中间低，边缘高；最高点在流域西部与房县交接处(房县大湾沟村)。流域属于局地性暴雨和连阴雨高发区，年降水量1100 mm，经常发生溪河洪水、泥石流以及滑坡灾害，其中2012年8月4日至5日，28个小时内官山镇普降暴雨达340毫米，造成百年一遇的洪涝灾害。

流域主要有官山河、袁家河、吕家河、西河4条河流，最长河流长度约14.2 km，河流总长度268.5 km，河网密度约0.84 km/km²。流域内有大马站、袁家河站和西河站三个气象站，孤山站一个水文站(如图2)。站点权重如表1所示。

3.2. 模型应用与结果比较分析

利用流域1973~1987年逐日逐时水文资料以纳什效率系数作为目标函数对三个模型参数进行率定，资料来源于《长江流域水文资料》。并选取15场洪水用已优选参数进行模拟，模拟结果见表2，选取部分场次洪水模拟过程作图，结果见图3~图8。

对于洪峰流量模拟平均相对误差，新安江模型、TOPMODEL模型和改进的SCS模型相对误差分别为38.33%、23.14%、37.26%，TOPMODEL模型 > 新安江模型 > 改进的SCS模型，TOPMODEL模型对洪峰流量模拟结果较好，新安江模型次之；对于峰现时间合格率，新安江模型、TOPMODEL模型和改进的SCS模型合格率分别为73%、93%、93%，改进的SCS模型 = TOPMODEL模型 > 新安江模型，改进的SCS模型和TOPMODEL模型对于峰现时间模拟较好；对于洪水洪量平均相对误差，新安江模型、TOPMODEL模型和改进的SCS模型相对误差分别为37.33%、38.28%、20.73%，改进的SCS模型 > 新安江模型 > TOPMODEL模型，改进的SCS模型对洪量模拟较好，新安江模型次之。从图4中可以看出，实测洪水洪峰与降雨过程存在不一致性，持续有降雨发生，实测流量出现第一个洪峰后陡落，与实际情况不符；而且从19790912场次与其它场次洪水图对比可以看出模

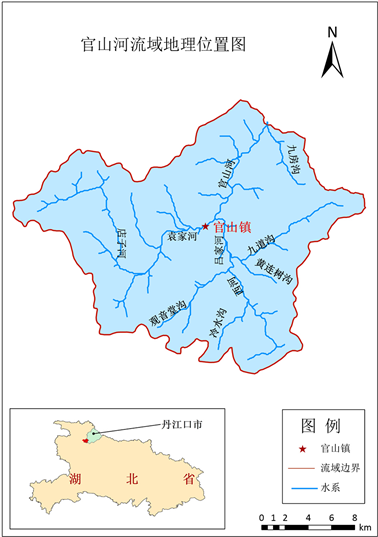
Figure 1. Administrative division map of Guanshan river basin

图1.官山河流域地理位置图

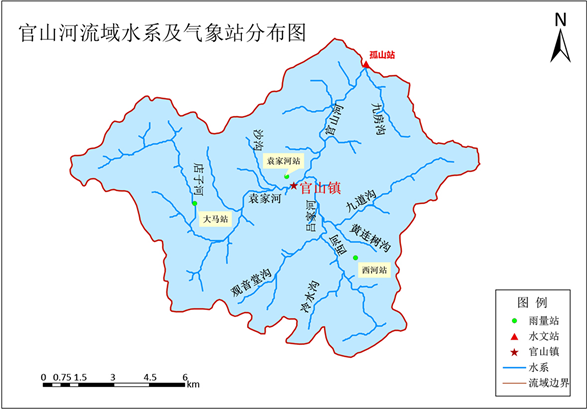
Figure 2. Sketch map of water system and meteorological station at Guanshan river basin

图2. 官山河流域水系及气象站分布图

Table 1. Control area and weight table of each station in Guanshan river basin

表1. 官山河流域各站控制面积及权重表

型对“单峰型”洪水模拟结果较好，而对“多峰型”洪水模拟结果较差。下面将简单分析一下各模型的适用性。

1) 改进的SCS模型。首先改进的SCS模型结构简单，参数少，对数据要求不太高，较适用于这种水文资料不够精准的小流域。许多研究者指出在暴雨径流中地下径流的重要性，如Hewlett等由试验发现了非饱和流也能形成壤中径流或地下径流，并且由Dunne等证实了非均质包气带确实具备产生壤中径流的条件 [20] 。改进的SCS模型为超渗产流机制，在土壤毛细管含水量未达到饱和时下渗的静态部分依旧能形成地下径流，从而对洪量模拟较好，也说明研究区场次洪水中地下径流贡献较大，存在突发暴雨时土壤含水量未饱和而形成地下径流的可能。

2) TOPMODEL模型。首先TOPMODEL模型为蓄满产流，当研究区降雨强度不大时，也会产生地表径流；其次TOPMODEL模型利用空间地形指数来反映流域地形的变化，将流域地形、地貌等纳入模型考虑范围内，在地形起伏较大的山区洪水汇流中有一定优势。TOPMODEL对洪峰流量模拟较好可能有这方面的原因。

3) 新安江模型。新安江模型模拟效果没有那么好是因为其是集总式模型，用在大流域模拟较多，对资料精度要求较高，当雨量站在空间分布不均匀或降雨具有空间不均匀性时，模型模拟就存在局限性，而且这种短时临近暴雨洪水具有极强的非线性性，新安江模型汇流采用的是线性汇流关系，因此模拟效果相对较差。

Table 2. Simulation results of the three hydrological models in Guanshan river basin

表2. 三种水文模型在官山河流域模拟结果

注：表中峰现时间为正值表示提前，负值表示滞后。

Figure 3. 19770718 simulation process hydrographs

图3. 19770718场次洪水模拟过程线

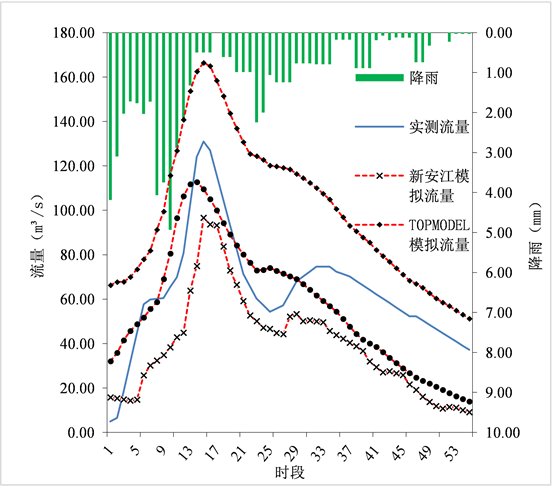
Figure 4. 19790912 simulation process hydrographs

图4. 19790912场次洪水模拟过程线

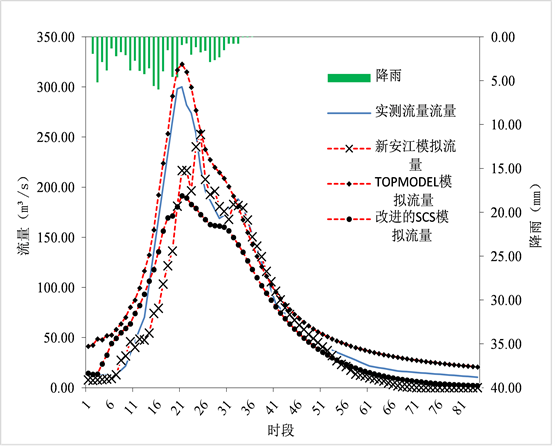
Figure 5. 19820824 simulation process hydrographs

图5. 19820824场次洪水模拟过程线

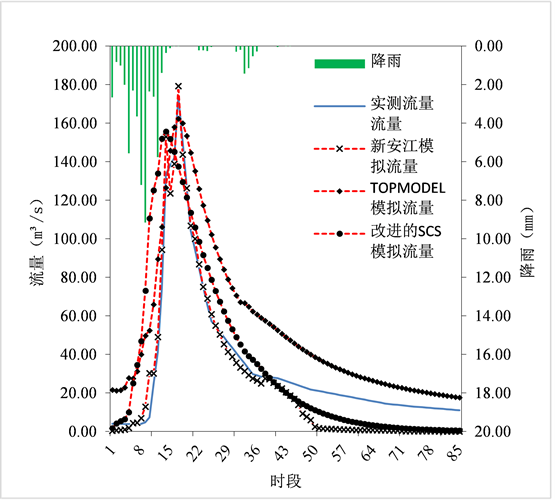
Figure 6. 19830916 simulation process hydrographs

图6. 19830916场次洪水模拟过程线

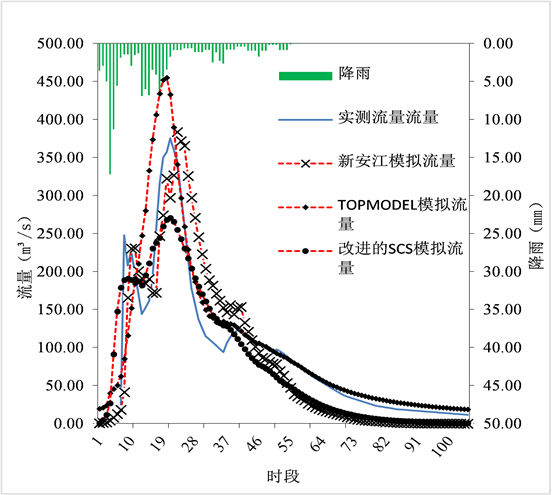
Figure 7. 19831005 simulation process hydrographs

图7. 19831005场次洪水模拟过程线

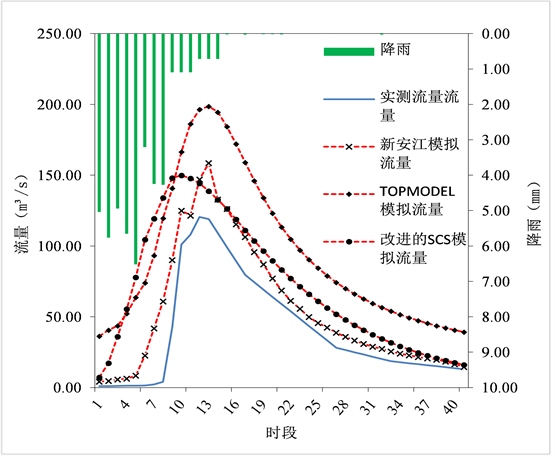
Figure 8. 19850621 simulation process hydrographs

图8. 19850621场次洪水模拟过程线

4. 结论及展望

1) 官山河流域有大马站、袁家河站、西河站、孤山站四个雨量站，各站控制面积分别为106.79 km²、71.29 km²、88.69 km²、52.78 km²。据《水文站网规划技术导则》，布站时，要求雨量站控制流域面积不能超过60 km²，山洪频发区不大于30 km² [21] 。由于地形、经济、技术等各方面的原因，目前流域雨量站分布密度较低，现利用降雨资料代表性较低。山区小流域的降雨具有极强的空间变异性，有限的雨量站无法较为准确地记录降雨量，而降雨的时空不均匀性对产流影响较大。而且利用的逐时刻降雨径流数据是从非连续时间记录的洪水要素资料中插值而得，也会影响水文模型模拟精度。降雨资料不精准使得从模型输入端便开始引入误差，因此必须综合运用遥感、雷达测雨和地面监测等技术，研究多源数据的同化、融合方法，重点构建点面结合的山洪多要素立体精准监测技术与体系，使得降雨资料具有代表性，从而提高模型模拟精度。

2) 官山河流域高程在240~1606 m间变化，有深沟陡坡，有暴雨发生时，在汇流过程中会利于产流迅速汇集，汇流时间短，从而形成山洪灾害危及中下游平缓地带。因此在今后的研究中不可忽视流域地形的影响。

3) 在模型模拟实测流量过程中发现，模型对流域前期土壤含水量较为敏感，但前期土壤含水量规律比较复杂。流域主要土壤类型为砂土，透水性能较好，储水能力较大，在场次洪水退水阶段地下水对径流补给量大，使得场次洪水出现陡涨缓落情况，在连续场次洪水综合作用下，便会造成山洪灾害。因此必须探清该流域的地质地貌，为构建适用于该流域的水文模型提供基础资料。

4) 所用的几个典型水文模型汇流采用的是线性汇流模型，瞬时单位线是从大中流域中总结出的方法，而山洪汇流过程具有极强的非线性性，汇流所用的单峰单位线也会对多峰洪水模拟效果欠佳。因此必须考虑不同的汇流方式对洪水预报精度的影响。

5) 半分布式模型相对于集总式模型有较大优势。TOPMODEL半分布式模型考虑了流域的地理信息，但是其假设降雨在空间是均匀分布的，这与实际不符。在今后的研究中应当构建更为合理的分布式水文模型来研究山洪模拟。

6) 流域的产汇流机制复杂。官山河流域可能不是单一的蓄满产流机制或者超渗产流机制，或者是保持一种产流模式不变，可能是各种产流机制相互转化相互补充。因此必须弄清流域复杂的产流机制，才能提高山洪预报精度。

基金项目

本文由国家重点研发计划(No. 2017YFC1502503)和国家自然科学基金重大项目(No. 41790431)资助。