1. 引言
人类基因组计划(Human Genome Project, HGP) [1] 是科学史上的三大伟大计划之一,生物信息学是为了应对计划中的基因测序问题而产生的一门学科。众所周知,蛋白质是生命系统中生命体进行生命活动的主宰者,是生命体不可或缺的一部分。目前,研究蛋白质的结构和功能已经成为生物信息学研究的一个重要的领域。此前为了得到蛋白质的结构主要是运用实验方法,如X射线晶体衍射和核磁共振的方法等 [2] 。但是,现实中最大的问题是我们生命系统中绝大部分的蛋白质的结构是不能用实验方法得到的,所以只能用人工智能预测其结构。所以,蛋白质二级结构预测课题应运而生。所谓蛋白质二级结构的预测 [3] ,其最重要的步骤是首先归纳我们已经知道结构的蛋白质序列,然后进行预测,预测时主要用到的是统计学方法和目前新兴的人工智能算法等。所以,在蛋白质二级结构发展的今天,已经出现了很多用来预测蛋白质二级结构的方法,如神经网络方法 [4] 、隐马尔可夫模型 [5] 方法等。
深度学习 [6] 是机器学习算法中人工神经网络研究衍生出的一个新的方法,其概念是在2006年被提出来的。其包含多种算法,如自动编码器 [7] 、深信度网络 [8] 及卷积神经网络等。卷积神经网络分类识别算法是由Yann LeCun等人 [9] 最早提出并应用在手写字体识别上的。卷积神经网络主要是用权值共享的思想降低网络学习的复杂度。本文提出了一种改进的卷积神经网络和Softmax [10] 相结合的方法,构建了一个10层的卷积神经网络,先用卷积神经网络对蛋白质二级结构的特征进行提取,把进入全连接层前的特征输入到Softmax分类器中,对提取到的特征进行分类预测实验。结果显示,本文的方法在25PDB (Protein Data Bank,简称PDB)数据集上的预测准确率有提高。
2. 基于卷积神经网络和Softmax的蛋白质二级结构预测
2.1. 卷积神经网络原理
近年来,随着深度学习算法的不断发展,卷积神经网络引起了广大研究者的关注。卷积神经网络(Convolutional Neural Networks, CNN) [11] 的概念是上世纪60年代Hubel和Wiesel [12] 两位研究者在研究神经元的时候发现的一种独特的网络结构,其独特之处在于卷积神经网络可以有效地降低网络的复杂性。卷积神经网络通过卷积和池化操作能很好地提取到输入数据的关键特征,所以目前卷积神经网络在模式分类领域中得到了广泛的关注和应用。CNN卷积过程的数学表达式如下所示:
(1)
公式中,n_in是输入数据组成的矩阵个数,Xk是第k个的输入矩阵。Wk则是卷积过程中我们选取的卷积核里的第k个子卷积核矩阵。
表示的是卷积核W对应位置的元素在其输出矩阵中的值。
卷积神经网络的基本结构包括卷积层、池化层和全连接层。卷积层主要执行的是卷积操作,其中用到的方法主要是局部连接和权值共享的方法,主要是在模拟大脑中有局部感受野的细胞,从而能够从获得的信息中提取出一些初级特征的过程。池化层主要执行的是下采样操作,包括最大值池化和平均池化等方法。输入的数据经过池化层的下采样操作后,输出的数据矩阵会变小,但是数量不变,所以池化层能够对从上一层的卷积层中输出的数据进行压缩,这样就能减小计算的复杂度、从而使学习参数数量减少,同时能有效地防止过拟合问题。在卷积神经网络模型中,最后的一层或是几层就是全连接层,全连接层的主要功能是对前面卷积和池化操作提取的特征进行加权求和,能够保证输入的数据在进行池化操作后保留下来的少量数据特征能够尽可能的重现原来的输入数据。
图1中,input为数据以矩阵的形式输入卷积神经网络,输入的数据进行卷积操作,得到C1层,C1层的数据进行下采样操作,得到S1层,卷积神经网络完成第一次卷积、下采样操作。第一次卷积—下采样操作的输出作为下一次卷积操作的输入,进行第二次卷积、下采样操作,以此类推,直到最后一次卷积操作完成,把卷积、下采样后得到的特征进行全连接并作为卷积神经网络提取特征的输出,把输出的数据输入到分类器中进行分类,得到我们所需要的分类结果。

Figure 1. Convolutional neural network structure
图1. 卷积神经网络结构图
2.2. Softmax回归模型
传统的逻辑回归模型主要处理的是二分类的问题,如Logistic回归模型 [13] 。面对多分类问题时,传统的逻辑回归模型不能满足分类需要,继而衍生出了一种用于多分类问题的回归模型——Softmax回归模型。传统的逻辑回归模型函数为:
(2)
其损失函数对应如下:
(3)
其中,
是输入的样本数据,
是对应的标签数据,θ是训练的模型参数,m是样本的总数,因为传统的逻辑回归应用于二分类问题,所以m的取值为2。在多分类问题中,我们用到的是Softmax回归,其中
可以取
个值,对应的m取值为k。
对于给定的输入x,针对每一个类别j估算出其概率值
。也就是说,针对每一种分类的结果估算其出现的概率。所以,对于
时回归模型函数的形式如下:
(4)
为了使公式看起来更加简便,用
表示全部的模型参数,在Softmax回归中,把
按行排列组成一个矩阵
,如下所示:
(5)
Softmax回归所对应的损失函数如下所示:
(6)
在上面的公式中,
表示的是示性函数。
从以上可以推出,对于给定的输入数据x,针对每一个类别j估算出的其概率值
如下所示:
(7)
2.3. 卷积神经网络和Softmax网络模型
为了简化计算量和解决反向传播时出现的梯度消失问题,在卷积层之后加入了Relu激活层。本文的网络结构包括输入层、卷积层、池化层、Relu激活层和全连接层。一般的卷积神经网络是在全连接之后,对所提取的特征进行分类预测,本文是提取第三层卷积层之后的特征,输入到Softmax分类器中进行训练和预测。
主要的网络结构图和参数设置如图2所示。
3. 实验和分析
主要介绍蛋白质数据库以及本文的实验过程和结果分析。
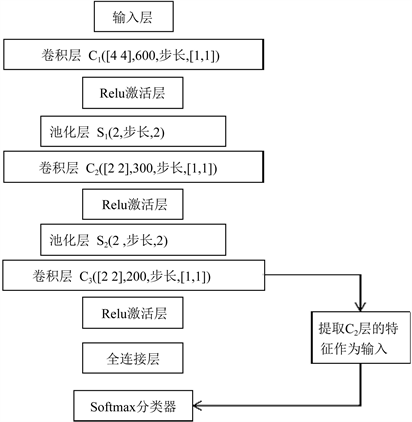
Figure 2. Convolutional neural network-Softmax network structure
图2. 卷积神经网络–Softmax网络结构图
3.1. 蛋白质数据库
在蛋白质二级结构预测的研究中,非同源蛋白质数据集25PDB数据集经常被用到。我们用本文提出的方法在25PDB数据集上做了交叉验证 [14] ,并把交叉验证的结果和其他方法做了比较。25PDB数据集包含了1673条相似性不超过25%的蛋白质序列。我们在准确率测试方面,是基于3-折交叉验证(3-fold cross validation)。
通过位置特异性叠代BLAST (Position-Specific Iterated BLAST, PSI-BLAST)程序进调用三次迭代并进行序列的对比就能获得位置特异性打分矩阵(Position-Specific Scoring Matrix, PSSM) [15] 。PSSM矩阵包含了物种的进化信息,同时其特有的滑动窗口技术保留了蛋白质序列中相邻氨基酸的关系。多序列比对 [16] ,从字面意思理解就是我们利用蛋白质序列的相似性对序列进行对比。实际操作中,我们很难知道每一个蛋白质序列的结构和组成,这就要求我们从NCBT nr数据库中搜索与其相关的同源序列的信息,预测我们所需蛋白质的结构。主要的操作是运行PSI-BLAST程序从NCBT nr数据库中搜索到25PDB相关蛋白质的同源序列信息之后,生成对应的20 * 13的PSSM矩阵。把PSSM矩阵用于蛋白质二级结构预测时,要选择一个滑动窗口,本文我们用到的滑动窗口大小为13,沿着PSSM矩阵每滑动一次,就可以提取出一个20 * 13的特征向量,即生成一个260维的特征向量。
3.2. 实验过程
首先通过运行PSI-BLAST程序搜索nr数据库生成对应PSSM矩阵。用大小为13的滑动窗口沿着PSSM矩阵中的蛋白质序列滑动,得到了一个260维的数据。把数据作为卷积神经网络的输入,用3 * 3的卷积核对数据进行卷积操作,经过3次卷积操作,把卷积神经网络第三次卷积后提取到的特征输出作为Softmax分类器的输入,用Softmax对提取的特征进行训练和预测,得到预测结果也就是蛋白质二级结构的三种形式:C (卷曲)、E (链残基)和H (卷曲)。主要的流程图如图3所示:
在数据处理的滑动窗口选择和在卷积神经网络提取特征时卷积核大小的选择上我们做了反复多次试验。在处理PSSM矩阵时,我们分别选取了9、11、13、15和17作为滑动窗口的大小,分别得到了数据维数为180维、220维、260维、300维和340维的矩阵,经过实验得出,滑动窗口大小为13的时候,预测的效果是最好的。在卷积核大小的选择上,我们分别以2 * 2,3 * 3,4 * 4和5 * 5作为卷积核的大小进行实验,最后我们设置的卷积层分别是600个4 * 4的卷积核、300个2 * 2的卷积核和200个2 * 2的卷积核。
3.3. 实验结果及分析
一个预测算法的好坏主要是通过衡量其预测精度来决定的。蛋白质二级结构的预测精度可以对正确预测的螺旋和折叠数量来进行计算。本文用到的衡量的方法是Q3和片段重叠准确率(Segment Overlap Score, SOV)方法。
Q3是被用于残基上的,通过计算正确预测的蛋白质残基占已知蛋白质二级结构序列中总的残基数的比例计算出。Q3值的范围为
,1表示准确预测。Q3就可以表示为:
(8)
SOV方法是由Burkhard Rost [17] 等人提出的一个基于重叠片段比值的测度。与Q3正确率的计算方法不同的是,SOV方法计算的是能够正确预测蛋白质二级结构的片段比例,从影响因素的角度来看,SOV会忽略一些蛋白质二级结构元素末端的小错误。
本文把25PDB数据集分成三份并编号为1、2和3,选择其中的一份作为训练集,剩余的两份作为测试集。我们依次以1、2和3作为测试集,用传统的卷积神经网络和本文的网络结构对其进行了训练和预测,得到了Q3和SOV的平均值。
对于本文用到的25PDB数据集,只使用卷积神经网络对训练集和测试集进行分类预测的Q3正确率和SOV如下表1所示:

Table 1. The results of convolutional neural network
表1. 卷积神经网络预测结果
对于25PDB数据集,先使用改进的卷积神经网络进行特征提取,再提取第三层卷积层的特征输入到softmax分类器中进行分类预测的Q3正确率和SOV如下表2所示:

Table 2. The results of convolutional neural network-Softmax
表2. 卷积神经网络和Softmax预测结果
从上表预测结果可以看出,对于蛋白质数据集25PDB,只使用传统的卷积神经网络对蛋白质数据进行分类预测,在训练集上的Q3正确率是76.96%,在测试集上的Q3正确率是75.90%,本文的方法是在传统的卷积神经网络中加入了Relu激活层,对蛋白质数据集进行特征提取,把卷积神经网络第三次卷积得到的特征作为Softmax分类器的输入对特征数据进行分类预测,在训练集上的Q3正确率是78.37%,在测试集上的Q3正确率是77.06%。本文的方法相较于经典的卷积神经网络方法在训练集和测试集上Q3平均预测精度分别提高了1.14%和1.16%。因为自动编码器可以不断调整它的各层的参数,得到每一层的权重,因而能够捕捉可以代表输入数据的最重要的因素,是一种尽可能复现输入信号的神经网络,所以预测结果提高了。但是自动编码器没有全局优化,输入的重建可能不是学习通用表征的理想度量,所以预测正确率的提高不是很明显。
4. 总结
本文结合了改进了卷积神经网络方法,在传统的卷积神经网络方法中加入了Relu激活层,简化了计算量并优化了梯度消失问题,直接提取第三层卷积层的特征作为输出,在分类预测方面引入了Softmax分类函数。把改进的卷积神经网络对蛋白质数据集25PDB经过卷积层、Relu激活层和池化层之后提取到的第三层卷积后的特征作为Softmax分类器的输入,用Softmax分类器对提取到的特征进行训练和预测。从表1和表2中可以看出只用卷积神经网络对25PDB数据集进行训练和预测的Q3和SOV分别是75.90%和71.98%,在本文的方法中的Q3和SOV分别是77.06%和72.99%,预测结果都有提高。卷积神经网络通过卷积和下采样操作能最大程度地提取到数据重要的信息,本文的方法在卷积神经网络中加入了Relu激活层,并把第三层卷积提取到的特征直接作为Softmax分类器的输入,最大程度地保留了原始信息,简化了计算量并解决了梯度消失问题。所以提高了预测结果的精度。
基金项目
本研究获得山东省自然科学基金(No. ZR2017LB024)项目资助。