1. 引言
液滴碰撞壁面的效应,在化工流体流动、飞机动力学、石油开采、喷墨印刷、农药喷洒、焊接熔接等领域有着重要的应用,人们大都关注液滴碰壁后的形貌演化和其能量转化,其中液滴碰壁后的最大铺展系数是研究的重要参数之一。
液滴碰壁可演化为多种形式,如碰撞水平壁面、球型壁面或管状壁面;进行垂直碰撞、倾斜碰撞或水平碰撞;进行常温碰撞、高温碰撞、过冷或过热碰撞,或进行超疏水壁面碰撞或植物液面碰撞等等。在所有的碰撞形式中,液滴在常温下碰撞水平壁面是最基础的碰撞模式,对其最大铺展系数问题,前人做了大量的研究工作,并总结出许多半经验公式(见表1)。

Table 1. Semi-empirical Formula for Maximum Spread Coefficient
表1. 最大铺展系数的半经验公式
求解最大铺展系数的过程,核心是建立能量守恒方程,一般情况下,方程左边是宏观能量差值,方程右边是能量损耗项。大多数研究中,宏观能量差值包含了机械能差值和内能差值,能量损耗项仅关注粘性耗散,并在处理粘性耗散函数中引入大量假设或近似公式。
将液滴和壁面看作一个系统,在铺展过程的任意时刻,由表面能、吸附能和变形能组成的系统内能项是守恒的,因此宏观能量差值不应有内能,而应仅有机械能项 [13] 。在建立液滴的流体力学模型后,能量损耗可进行完整的理论推导。同时,在干态铺展中,能量损耗中占到主导作用的应是三相接触线损耗,而不是通常认为的粘性损耗,因此,三相接触线损耗是不能忽略的。
在此思路下,通过圆柱型液滴的假设,利用轴对称不可压缩驻点流动模型,重新对最大铺展系数进行了理论推导,并得出了较为满意的结果。
2. 假设模型
2.1. 无纲量参数
将液滴碰撞水平壁面的过程分解成3个过程。并引入以下无纲量参数:
铺展系数:
比速度:
比能:
雷诺数:
韦伯数:
付鲁德数:
邦德数:
式中:r:液滴铺展半径;r0:球型液滴初始半径;UR:三相接触线速度;U0:液滴撞击壁面时的速度;ED0:液滴初始动能;ρ:液滴密度;μ:液滴粘度;γL:液滴表面张力;g:重力加速度。
2.2. 跌落过程
过程1为液滴的跌落过程,半径为r0球状液滴进行跌落,和水平壁面距离为零时跌落过程结束,此时液滴速度为U0。
当液滴为球型时,液滴的初始机械能EJ0为动能ED0、附加压力能EY0和势能ES0的和:
(1)
因此液滴的初始比能为
(2)
将液滴变形为半径为R1,高度为H1的圆柱体,变形前后液滴的内能守恒,令液滴变形前后机械能相等,因动能未在变形过程中发生变化,因此可得:
(3)
整理可得:
(4)
即:
(5)
因
,可得
。
2.3. 碰撞过程
过程2为液滴的碰撞过程。以圆柱状液滴底面圆心为零点,建立r-h-θ的柱坐标系,并假设:
a) 在碰撞过程中液滴形状不发生变化;
b) 碰撞过程中动能守恒,液滴的垂直速度Uh转化为水平速度Ur;
c) UH2等于零时碰撞结束。
根据圆柱体在不同方向上的体积微分可知:
(6)
可解得:
(7)
假设液滴铺展过程中保持圆柱状,在任意r处的环形截面,其单位时刻的体积流量应保持相等,即:
(8)
考虑到公式(7) (8)的形式,可以假设液滴在铺展过程中的速度分布满足:
(9)
在铺展的确定时刻,a为比例常数。因此可以将铺展过程看作轴对称驻点流动的类型。以圆柱状液滴顶面的垂直速度UH和三相接触线速度UR表示,液滴动能方程可表示为:
(10)
碰撞结束时,
,可解得
。
2.4. 铺展过程
过程3为液滴的铺展过程。液滴在初始机械能的作用下进行铺展,在壁面摩擦力和粘性耗散的作用下减速至零,此时的液滴半径Rmax对应最大铺展系数βmax。
在铺展的任意时刻,液滴的比能为:
(11)
3. 理论推导
液滴铺展过程中系统内能守恒,液滴必然具备压缩性。但由于其压缩比很低,可以近似认为铺展过程是不可压缩流动。液滴的铺展过程是非定常流动,定常流动解可看作是该流动的零阶近似。根据K Hiemenz假设 [14] ,定常不可压缩轴对称驻点流动的粘性流动速率满足:
(12)
该流体的N-S方程可变形为:
(13)
方程的边界条件为:
(14)
其中:
根据边界层理论,轴对称驻点流动的边界层厚度为:
(15)
式中边界层厚度系数
。
铺展过程的能量耗散由粘性耗散、三相线耗散和前驱膜耗散组成。忽略前驱膜的耗散,铺展过程的比能量守恒方程可表述为:
(16)
3.1. 粘性耗散
柱坐标下粘性耗散函数
可表示为 [15] :
(17)
将各关系式带入整理可得
(18)
和右边第二项相比,右边第一项为小量,可以忽略,因此粘性耗散函数可简化为:
(19)
耗散函数的体积积分
为:
(20)
记
,则
(21)
公式(13)无解析解,N.Fröessling [16] 给出了数值解,利用该数值解,可求得
。
液滴铺展过程的粘性损耗比能可表示为:
(22)
3.2. 三相线耗散
虽然在K Hiemenz假设下,液滴和壁面的接触面存在滑移,壁面摩擦力会造成损耗,但其滑移位移不可解,我们仅考虑三相接触线的移动造成的摩擦损耗,而忽略接触面滑移损耗。
三相接触线处,壁面的切应力:
(23)
其中
半径为dR的圆柱体,其单元三相线摩擦力可表述为:
(24)
三相线摩擦力的耗散比能为
(25)
3.3. 铺展速度
能量守恒方程(16)本身是无法求解的,为了简化计算,我们忽略铺展过程中的垂直动能、残余附加压力能和残余势能,由式(16) (22)和(25),并记:
可得:
(26)
将式(26)进行微分:
(27)
解该方程,得:
(28)
C为积分常数,将式(28)带入(26)可求得:
(29)
因此,液滴碰壁后的铺展速度满足方程:
(30)
公式(30)各项有着明确的物理意义。
是能量耗散系数,
是液滴的初始比能,β1是初始铺展系数,其他均为积分常数。
将式(30)分离变量,进行再次积分,可得到铺展系数β和时间t的关系,但由于其积分公式无法求解,我们只能近似得到关系:
(31)
这和通过标度分析得到的结果一致 [17] 。
3.4. 最大铺展系数
当液滴铺展到最大半径时,
,由式(30)可得:
(32)
将ω值带入,可知:
(33)
或:
(34)
在文献 [1] [3] [4] [10] 等的研究中,最大铺展系数βmax的幂次大都为2,这一差异均是在其估算能量耗散公式时,采用的各参数预估模型的误差导致。因此带来和雷诺数的幂次关系出现非0.2的现象。在文献 [1] [3] [4] [6] [10] [12] 等研究中,方程出现和接触角相关的关系,是由于在宏观能量差值中考虑了表面能或其他内能因素。如果去除这一问题,其方程均可变形为类似公式(34)的形式。
4. 数据验证
公式(32)并不适合产生飞溅、破碎和指进现象的撞击过程,因为飞溅和破碎现象带走了一部分机械能,导致方程(16)左边产生差异。指进现象没有统一的铺展系数。对于产生铺展、振荡、回缩甚至回弹现象的液滴碰壁过程,公式(32)均应有良好的解释力。
其次,公式(16)未考虑热交换过程,因此高温、过冷或过热情况下的液滴碰壁过程不适合公式(32)。
再次,轴对称驻点模型适应于边界层是层流的状态,光滑平板的临界雷诺数为3.5×105左右 [18] ,因此对于超过临界雷诺数的撞击,公式(32)不适用。
从13篇中外文献中提取了符合以上要求的84个实验数据 [10] [19] - [30] (见表2),液滴材质涉及水、乙醇、柴油、甘油、石蜡等多项物质,壁面材质涉及玻璃、不锈钢、铝、石蜡和塑料。液滴直径r0范围0.6~5.0 mm;碰撞速度U0范围0.5~4.37 m/s;雷诺数Re范围41~21698,韦伯数We范围9~1310;付鲁德数Fr范围8.5~1773.3;邦德数Bd范围0.01~0.84;最大铺展系数βmax范围1.16~5.79。
使用公式(32)对文献数据进行拟合(见图1),发现拟合度良好,计算值和实验值的相关系数R2 = 0.74,进行单因素方差检验,得出在显著性水平α = 0.05时,P = 0.57 > 0.05,F = 0.33 < 3.89,因此可认为计算值和实验值无显著差异。


Table 2. Application and calculation data of maximum spreading coefficient
表2. 最大铺展系数的应用数据和计算数据
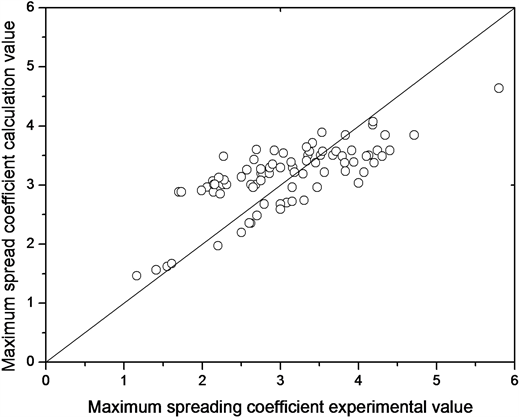
Figure 1. Comparisons between experimental and calculated values of βmax
图1. βmax的实验值和计算值的对比
对文献数据进行处理,拟合Re0.2和βmax,得到的关系式为(见图2):
(35)
其关系系数和公式(33)几乎无差异。
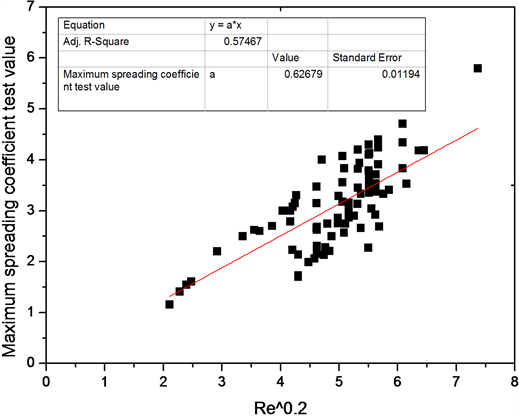
Figure 2. Experimental Value of βmax and Re0.2 Fitting Figure
图2. βmax实验值和Re0.2拟合图
5. 结论
1) 建立液滴碰撞壁面的过程假设,利用轴对称驻地流动模型,得出最大铺展系数的理论关系式,该关系式有明确的物理意义,具有良好的解释力。
2) 通过实验数据的对比,计算值和实验值有较强的符合性。