1. 引言
大量中小型桥梁的桥面系统采用钢筋混凝土梁,对此类梁结构进行准确分析是结构性能设计和保障桥梁安全服役的关键。传统的钢筋混凝土梁理论 [1] [2] [3] 忽略了混凝土局部受拉区的受力及其拉伸过程中的损伤,认为结构拉应力全部由钢筋承受。实际上,在服役初期,处于良好状态的混凝土在受拉区和钢筋共同承受荷载;随着服役期增长,当混凝土拉应力所引起的损伤达到损伤演化阈值,拉伸损伤导致细观裂纹萌生;当损伤达到失效临界值,细观裂纹发展为宏观裂纹,受拉区混凝土丧失承载力。考虑上述服役过程中混凝土真实的受力情况,发展一个符合结构真实性能演化过程的新的梁理论,才有可能实现对结构服役过程的准确模拟和分析。
鉴于梁服役过程中受力的复杂性,国内外学者部分致力于对梁受力机理和本构模型的研究 [4] [5] [6] ,部分采用数值方法 [7] [8] 描述结构的几何和物理构型对服役性能的影响,但建立一个较为准确的反映钢筋混凝土结构服役中损伤演变的解析理论一直进展较慢。好的解析模型不仅能方便土木工程师进行结构设计,也能进一步完善现有的钢筋混凝土的基本理论体系,因此,本文致力于建立一个考虑混凝土损伤演化的新型的梁理论,通过引入混凝土拉伸损伤,考虑实际服役过程中拉伸区混凝土的作用,以及钢筋和混凝土材料的非均质性。在此基础上,以挠度表征梁的耐久性,研究混凝土收缩和荷载长期效应对结构损伤演化和服役寿命的影响,获得修正的挠度计算公式,并进一步评估钢筋混凝土结构的服役寿命。
2. 考虑非均质和混凝土拉伸损伤性能的梁理论
传统的钢筋混凝土梁,相应的分析模型如图1所示。图1(a)为梁的受力,图1(b)为沿着高度方向,应变的分布情况,图1(c)对应钢筋和混凝土上的分布以及应力分布。保持钢筋截面面积不变,将受拉钢筋等效为等强度的钢筋层。
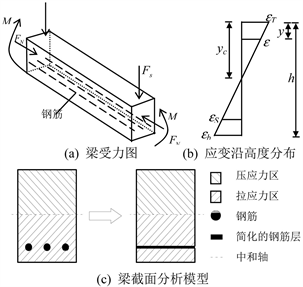
Figure 1. Schematic diagram of reinforced concrete beam model
图1. 钢筋混凝土梁分析模型示意图
对于混凝土,采用Mazars提出的标量损伤模型 [4] ,该模型认为峰值以前,混凝土即使存在损伤,应力应变近似服从线性分布;峰值以后,应变增长而应力呈指数函数下降,相应的表达式如式(1)所示:
(1)
(2)
式中,
为混凝土的弹性模量,依据文献 [9] ,取
,
为时间t时混凝土柱体的抗压强度,当混凝土龄期超过28天时,可取第28天时柱体达到的抗压强度值
计算。
分别为受拉或受压状态,
为损伤,采用公式(2)计算,
、
和
均为材料常数,由混凝土单轴试验确定;
为混凝土单轴应力–应变曲线的峰值应变,
为混凝土单轴应力–应变曲线的极限应变。
对于钢筋,采用理想弹塑性模型,如式(3)所示:
(3)
其中,
为钢筋材料的屈服应变,
为钢筋弹性模量。
根据配筋率不变原则,将钢筋等效为等强度的单层板,不考虑钢筋和混凝土相对滑移,该钢筋层满足经典板理论中的直法线假设、等法线假设、平面假设和线弹性小变形假设 [10] 。受载后的截面上的应变可表示为:
(4)
式中,
为梁截面任意一点的应变;
为混凝土顶端压应变;
为中性轴到混凝土顶端的距离。
用应力所表示的梁截面的力的平衡方程可表示为:
(5)
式中,
、
及
分别表示受压区混凝土、受拉区混凝土和等效钢筋的应力,
、
及bw分别为三者的面积。
用应力所表示的梁截面的矩的平衡方程可表示为:
(6)
将钢筋混凝土梁从完好到破坏的服役过程分为四个典型阶段加以考虑:
1) 拉伸区混凝土处于弹性阶段,即
时,结合式(1)、(2)~(6)可得中性轴距离混凝土顶端的距离
的值:
(7)
2) 拉伸区混凝土开始开裂,钢筋的应力不超过屈服极限,即
且
时,记混凝土受拉区开裂厚度为t,根据平面假设:
。结合式(1)~(6),并忽略方程中含有
的项,可得中性轴距离混凝土顶端的距离
的值:
(8)
式中,
在给定任意一个混凝土边缘处的压应变
的值时,即可得到相应的中性轴位置
。
3) 钢筋屈服,顶端混凝土未达到其压应变峰值,即
且
时,结合式(1)~(6),并方程中含有
的项,可得中性轴距离混凝土顶端的距离
的值:
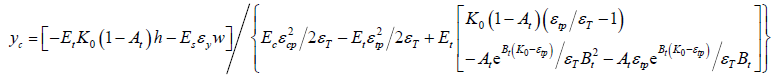 (9)
(9)
在给定任意一个混凝土边缘处的压应变
的值时,即可得到相应的中性轴位置
。
4) 顶端混凝土的应变超过其峰值压应变,即
时,记达到峰值压应变的混凝土厚度为p,则根据平截面假设有
,结合式(1)~(6)并忽略方程中含有
的项,可得中性轴距离混凝土顶端的距离
的值:
(10)
式中,
在给定任意一个混凝土边缘处的压应变
的值时,即可得到相应的中性轴位置
。
梁的极限弯矩对应于混凝土受压区边缘压应变达到极限压应变
的弯矩,结合上述式(10)中和轴
的公式,取
,可得梁的极限弯矩,如式(11)所示:
(11)
代入材料力学中纯弯曲变形时的曲率公式,可得:
(12)
因此,对于纯弯曲简支梁,相应的挠度计算公式为:
(13)
式(13)给出了等刚度的钢筋混凝土梁的挠度计算公式,式中梁的弯矩M由两部分组成:(1)自重引起的弯矩,记为
;(2)外荷载引起的梁截面的弯矩,记为MF。
实际上,由于各截面配筋不同,承受的弯矩也不等。弯矩小的截面可能不出现裂纹,其刚度要较弯矩大的开裂截面大,因此沿跨长方向抗弯刚度为变值 [7] 。同时,混凝土的密实性和开裂等因素对梁的挠度也有影响。因此,本文在公式(13)的基础上考虑了一个修正系数
,相应的梁挠度的计算值如式(14)所示:
(14)
对处于其他受力状态和约束条件的钢筋混凝土梁,可根据最小刚度原则 [2] 计算梁的挠度。
3. 考虑损伤演化的钢筋混凝土梁挠度和寿命计算模型
3.1. 考虑混凝土收缩的梁的曲率
文献 [11] 指出,一般地区的混凝土收缩应变的时变模型如式(15)所示:
(15)
式中,
、
为与构件尺寸相关的系数(见表1);t为服役时间。

Table 1. Coefficients of A 1 , A 2 , A 3 , A 4 [9]
表1. 系数
、
、
、
[9]
(注:Th = 2*截面面积/截面周长)。
相应的由混凝土收缩所引起的梁的曲率可表示为 [11] :
(16)
式中,
、
分别为受拉和受压钢筋的配筋百分率,h为截面高度,
见式(15)。
3.2. 考虑荷载长期效应的梁的曲率
式(7)~(10)给出了不同损伤状态下修正的中和轴
位置的表达式,若考虑式(1)的标量损伤模型,则在荷载短期效应组合下的钢筋混凝土梁截面曲率为:
(17)
将式(7)~(10)代入即可得到不同损伤状态下的短期效应下曲率的计算公式。
钢筋混凝土梁在使用阶段的曲率应考虑荷载长期效应,取文献 [9] 给出的一般地区的混凝土徐变系数来作为梁曲率长期增长系数,即:
(18)
式中,
、
为与构件尺寸相关的系数,见表1所示;
、
意义同式(16);
为服役时间;
为混凝土强度系数。
(19)
则考虑荷载长期效应的钢筋混凝土梁的曲率可表示为:
(20)
由此,可得计算钢筋混凝土梁挠度的通式
(21)
式中,K为不同支撑情况所对应的挠度系数,对于悬臂梁,取K = 0.5,对于简支梁,取K = 0.125;L为梁的计算跨径。只要通过测试获得梁截面顶端的压应变
,即可得到梁的曲率,进而获得其挠度。
《公路桥规》规定,钢筋混凝土受弯构件的长期挠度值,在消除由梁自重产生的长期挠度后,不应超过以下规定的限值 [12] :梁式桥主梁的最大挠度为
;梁式桥主梁的悬臂端的挠度不应超过
;此处,l为受弯构件的计算跨径,
为悬臂长度。因此,消除自重后的长期挠度为
(22)
式中,
为荷载短期效应组合下梁的曲率,见式(17);
为钢筋混凝土梁自重所引起的梁的曲率;
为由荷载引起的钢筋混凝土梁曲率的长期增长系数,见式(18)。
以混凝土挠度作为判别梁安全服役的指标,由规范给出的梁的最大挠度,代入公式(22),即可得到钢筋混凝土梁的安全服役寿命,相应的寿命分析流程如图2所示。
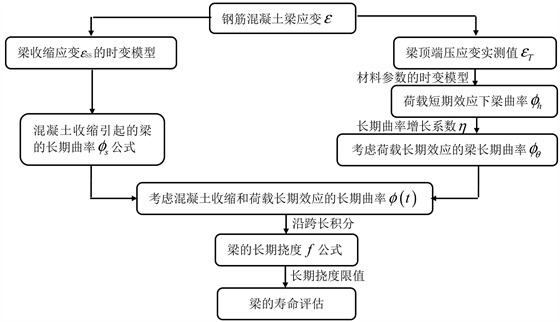
Figure 2. Flow of life assessment of reinforced concrete beams considering concrete shrinkage and load long-term effects
图2. 考虑混凝土收缩和荷载长期效应的钢筋混凝土梁寿命评估流程
4. 工程验证
4.1. 验证考虑非均质和混凝土拉伸损伤性能的梁理论正确性
分析图3的适筋梁,将其分析结果与试验结果对比来验证理论的正确性。该梁采用两点对称加载,量测钢筋和混凝土纵向应变的测点布置于跨中截面,跨中及支座处有位移计,用以测定跨中挠度。设钢筋截面中心至梁顶受压边缘的有效高度为
,截面宽度b = 150 mm,高度h = 350 mm,混凝土强度等级为C25,纵向受拉钢筋采用
,钢筋截面总面积
mm2 。
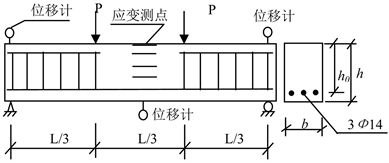
Figure 3. Schematic diagram of test of flexural performance of normal section [1]
图3. 正截面受弯性能测试示意图 [1]
仅在中跨区段下部配置受拉钢筋而不设架立钢筋,因此该段为纯弯曲段,采用逐级加载记录梁开始受载直至正截面破坏的整个试验过程中,裂纹的出现、扩展及其分布情况,同时绘出由本文计算公式和试验所得到的相对弯矩与中和轴相对高度以及相对弯矩与跨中挠度的关系曲线,分别如图4和图5所示。
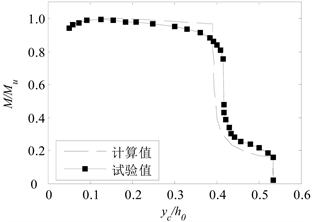
Figure 4. Relation between position of neutral axis yc/h0 and M/Mu
图4. 中和轴相对位置yc/h0与M/Mu的关系曲线
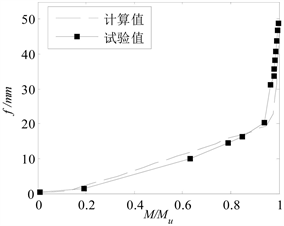
Figure 5. Relation between M/Mu and deflection f in mid-span
图5. M/Mu与跨中挠度f的关系曲线
图4表明,所建立的梁理论所计算的不同的中和轴相对位置与弯矩的相对值的关系与试验值基本吻合,误差在1%~5%之间。开始加载时,弯矩很小,开始加载时,弯矩很小,中和轴
,略大于
的位置,挠度–弯矩为直线,说明挠度与弯矩成正比,认为试件处于弹性阶段。弯矩增大,当拉伸区混凝土拉应变达到开裂应变阈值,受拉区边缘出现裂缝,此时的弯矩为开裂弯矩
,本算例中
,试验值为
,误差为8.9%,其中
为极限弯矩。
分别取
(代表拉伸区混凝土未开裂阶段)和
(拉伸区混凝土裂纹萌生并扩展),采用式(14)计算跨中挠度,相应的相对弯矩与挠度的关系曲线如图5所示。可以看出,计算值与试验值基本吻合,误差在1%~10%之间。随着荷载增加,曲线斜率增大,说明梁的刚度逐渐减小,与实际情况吻合,表明考虑修正系数
的梁的挠度计算是合理的,能较准确地反映梁跨中挠度的变化规律。在达到
瞬间,图中曲线出现第一个转折点,随后,荷载增加,相应的中和轴开始上升。荷载继续增加,受拉区截面的损伤不断增大,已有裂缝宽度增大并向梁顶扩展;此时,中和轴、应力和曲率都呈稳定增长趋势,挠度–弯矩曲线大致呈线性,斜率相对于开裂弯矩前的斜率增加,表明此时梁截面的抗弯刚度较之前下降。当荷载继续增加至钢筋应变达到屈服应变,受拉区混凝土大部分开裂,只有靠近中和轴附近的小部分未开裂;荷载继续增加,钢筋应力不变,压缩去混凝土压应变逐渐得到峰值压应变,混凝土逐步进入软化阶段,弯矩稍有增加,跨中挠度显著增长。位于不同截面高度的点处,相对弯矩–损伤的关系图线如图6所示。可以看出,距离上顶端越远,
值越大,相应的损伤值越大,当压缩区混凝土逐渐达到峰值压应变,损伤值逐渐趋于1,试件随着混凝土压碎而破坏,此时的弯矩为极限弯矩
。以上结果与适筋梁正截面受弯试验结果吻合 [1] [2] 。
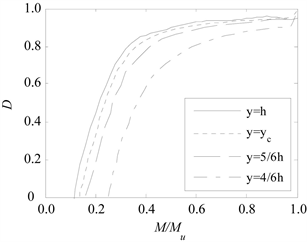
Figure 6. Relation between D and M/Mu
图6. 不同截面高度的损伤D与弯矩相对值的关系曲线
4.2. 验证寿命分析模型正确性
为了验证寿命分析模型的正确性,借鉴悉尼理工大学的单筋矩形梁服役650天的挠度试验结果 [9] 。梁截面为100 mm × 150 mm的矩形截面,底部配有
钢筋(钢筋为I级钢,
GPa),28天时混凝土圆柱体抗压强度
N/mm2,加载示意图见图7所示,28天后加载的实测挠度值见表2,为了比较,表2中也列出采用本文公式所得到的挠度计算值。
1) 钢筋混凝土梁的曲率
以服役500天为例,依据自重q和荷载P计算混凝土梁顶端的应变值
。
混凝土弹性模量:
梁截面惯性矩:
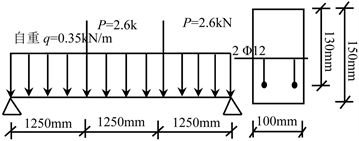
Figure 7. Loading diagram of beam [9]
图7. 加载示意图 [9]

Table 2. Comparison of calculated value and measured value [9]
表2. 跨中挠度计算值与实测值 [9] 比较
由自重q引起的梁跨中截面弯矩:
由荷载P引起的梁跨中截面弯矩:
跨中截面的总弯矩为:
荷载引起的钢筋混凝土梁顶应变
由荷载引起的短期曲率按式(19)计算:
因
,查表1并线性内插即可得
,
,
,
配筋率
,
因此,长期曲率
由于
,由式(16)可得:
混凝土收缩所引起的钢筋混凝土梁的曲率:
钢筋混凝土梁的总的曲率:
2) 钢筋混凝土梁挠度
取该简支梁
,由式(22)得:服役500天时,该钢筋混凝土梁的挠度:
由表2可见,计算值与实测值的误差在2%~15%内,具有一定程度的准确性。
3) 钢筋混凝土寿命
本试验由荷载短期效应组合并考虑荷载长期效应影响产生的长期挠度值为:(取挠度长期增长系数 [9]
)
因此,应设置预拱度:
该钢筋混凝土梁安全服役的挠度应满足
解得:
认为该钢筋混凝土梁在设计使用年限内满足安全性要求。由表2可以看出,钢筋混凝土梁挠度的计算值比实测值要稍微偏大,因此,由公式计算的梁挠度偏为保守,安全服役寿命也稍保守。
5. 算例分析
5.1. 算例结构
某钢筋混凝土桥,按左右线分离式设计,左线某大桥起点桩号为ZK79 + 605.511,终点桩号为ZK79 + 906.311;右线某大桥起点桩号为YK79 + 568.6,终点桩号为YK79 + 869.4。大桥左右线主桥均由40 m + 70 m + 40 m预应力混凝土连续刚构组成,引桥为25 m预应力混凝土连续箱梁,桥梁全长300.8 m,箱梁截面图分别如图8和图9所示。
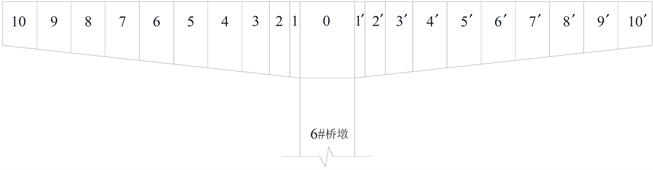
Figure 8. Longitudinal profile of box girder of bridge
图8. 主桥箱梁纵断面图
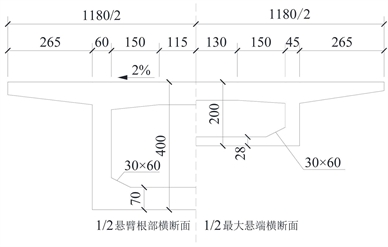
Figure 9. Cross section of box girder of bridge (unit: cm)
图9. 主桥箱梁横断面图(单位:cm)
主桥上部结构采用C55混凝土:标准强度
= 35.5 MPa,
= 2.74 MPa;纵向预应力钢束:采用美国标准ASTM A416-2002 270级高强低松弛钢绞线,单根绞线直径为15.2 mm,每股面积为140 mm2,标准强度
= 1860 MPa,最小破断荷载260.7 kN,张拉控制应力为
,主桥纵向预应力采用
和
钢绞线,纵向受拉钢筋截面的重心至受拉边缘的距离为
,钢筋混凝土梁配筋图如图10所示。运用ABAQUS建立了钢筋混凝土桥梁有限元损伤分析模型,其中钢筋混凝土梁采用solid单元建立,钢筋采用三维的wire单元来建立,钢筋嵌入在混凝土中。所建立的钢筋混凝土桥梁有限元损伤分析模型如图11所示。
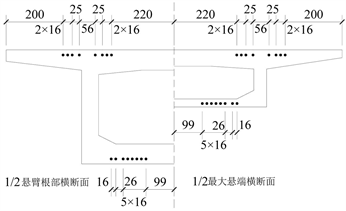
Figure 10. Reinforcement scheme (unit: cm)
图10. 钢筋混凝土梁配筋图(单位:cm)

Figure 11. Finite element model of reinforcement concrete beam
图11. 钢筋混凝土梁有限元模型
5.2. 算例结构塑性模型参数的确定
混凝土损伤塑性模型(Concrete Damage Plasticity)为连续的、基于塑性的混凝土损伤模型 [13] 。它假定混凝土材料主要因拉伸开裂和压缩破碎而破坏。应用该混凝土损伤塑性模型,最关键的是对混凝土材料的参数进行定义,分析模型的主要材料参数见表3。

Table 3. Material parameters of damage plastic model of concrete
表3. 混凝土损伤塑性模型材料参数
用Mazars混凝土损伤本构关系来拟合混凝土规范(GB 50010-2010)给出的混凝土本构关系,得Mazars损伤参数为:
,
,
,
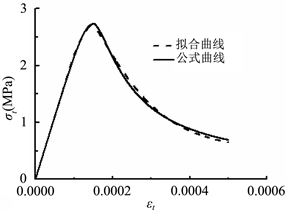
。拟合情况如图12所示。
 (a)
(a) 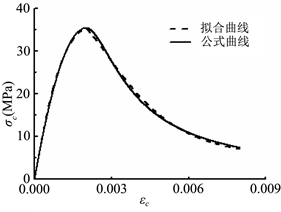 (b)
(b)
Figure 12. Constitutive relation curve of C55 concrete: (a) Stress-strain curve of concrete under uniaxial compression; (b) Stress-strain curve of concrete under uniaxial tension
图12. C55混凝土本构关系曲线:(a) 混凝土单轴受压应力–应变曲线;(b) 混凝土单轴受拉应力–应变曲线
由图13可以看出,采用Mazars提出的混凝土标量损伤本构模型结合拟合的损伤参数值所得到的混凝土应力–应变曲线与由规范公式得到的混凝土本构关系曲线非常接近,说明采用Mazars提出的混凝土标量损伤本构模型结合拟合的损伤参数值能较好地拟合混凝土的损伤本构关系。
 (a)
(a)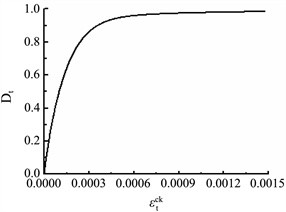 (b)
(b)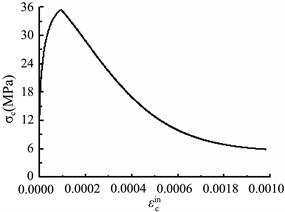 (c)
(c) 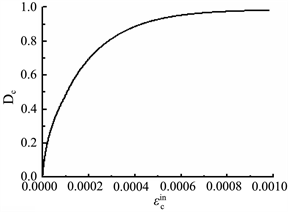 (d)
(d)
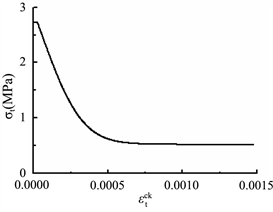
Figure 13. Parameters of C55 concrete during tensile hardening and compression softening: (a) Relation between inelastic tensile strain and damage; (b) Relation between inelastic tensile strain and yield stress; (c) Relation between inelastic compressive strain and damage; (d) Relation between inelastic compressive strain and yield stress
图13. C55混凝土拉伸硬化以及压缩软化参数设置:(a) 非弹性拉应变–拉伸损伤曲线;(b) 非弹性拉应变–屈服拉应力曲线;(c) 非弹性压应变–压缩损伤曲线;(d) 非弹性压应变–屈服压应力曲线
拉伸硬化与压缩软化是混凝土材料的重要属性,能否对混凝土的拉伸硬化与压缩软化参数进行准确的设置,关系到后续计算的成败与计算结果的准确性,所选取的混凝土拉伸硬化与压缩软化参数曲线见图13。
5.3. 车道荷载布置
交通部颁布的《公路工程技术标准》(JTG B01-2003)规定汽车荷载分为公路-I级和公路-II级两个等级,汽车荷载由车道荷载和车辆荷载组成。车道荷载由均布荷载和集中荷载组成,桥梁结构的整体计算采用车道荷载;对于桥梁结构的局部构件,加载采用车辆荷载。车道与车辆荷载的作用不得叠加。其汽车荷载与《公路桥梁通用设计规范》(JTG D60-2004)规定相同,车道荷载的计算图式如图14所示。
公路-I级车道荷载的均布荷载标准值
;集中荷载标准值按以下规定选取:桥梁计算跨径
时,
;
时,
;
时,
值采用直线内插求得。计算剪力效应时,
值应乘以1.2的系数。公路-II级按公路-I级的0.75倍采用。
5.4. 寿命分析
在4.1节所建立的钢筋混凝土梁上,施加如图14所示的设计荷载、重力和预应力,采用ABAQUS所计算的位移云图如图15所示,显示该钢筋混凝土梁在预应力、自重和车道荷载作用下的短期挠度为
。
受压区配筋率
受拉区配筋率
因为
,由表1线性内插可得
,
,
,
。
所以,混凝土收缩产生的钢筋混凝土梁的长期曲率:
混凝土收缩产生的钢筋混凝土梁的长期挠度:
由钢筋混凝土梁自重和荷载产生的钢筋混凝土梁长期挠度增长系数:
因此,由钢筋混凝土梁自重和运营荷载产生的钢筋混凝土梁的长期挠度:
考虑混凝土收缩的钢筋混凝土梁长期挠度值:
消除自重产生的长期挠度后的钢筋混凝土梁的长期挠度值:
《公路钢筋混凝土及预应力混凝土桥涵设计规范》 [12] 规定:当由荷载短期效应组合并考虑荷载长期效应影响产生的长期挠度超过计算跨径的
时,应设预拱度,且预拱度的值按梁自重和
活载所引起的长期挠度值来设定。
本试验钢筋混凝土梁由荷载短期效应组合并考虑荷载长期效应影响产生的长期挠度值为:(取挠度长期增长系数 [12]
)。
因此,应设置预拱度:
。
该钢筋混凝土梁安全服役的挠度应满足
即
解得
。
认为在该服役期内的钢筋混凝土梁满足安全性要求。
6. 结论
针对钢筋混凝土桥梁的主要部件——钢筋混凝土梁,建立了新型的钢筋混凝土梁模型并发展了新型的钢筋混凝土梁理论,选取桥梁挠度作为寿命指标,建立了寿命预测的公式。获得了如下结论:
1) 本文建立的钢筋混凝土梁模型可以方便地考虑混凝土拉伸区开裂和不同阶段的损伤演化过程,以及钢筋位置、数量对应力分布的影响;对于试件的开裂弯矩、屈服弯矩和极限弯矩,以及服役全过程中中性轴的位置变化均给出较为准确的量化关系式,试验值和测试值吻合较好,误差在1%~10%之间。
2) 建立了新的钢筋混凝土梁挠度的计算公式,可方便计算梁的长期挠度,误差在2%~15%以内;基于挠度计算公式,可获得钢筋混凝土梁的服役寿命。
3) 运用ABAQUS建立了某大桥钢筋混凝土变截面T箱梁的有限元模型,通过施加车道荷载,基于本文的桥梁寿命分析理论计算出该桥的使用寿命,结果表明,在设计使用期内,该桥可安全使用。
基金项目
本论文受国家自然科学基金资助项目(51678135, 51478108)、江苏省自然科学基金资助项目(BK20171350)、中央高校基本科研业务费专项资金资助项目(2242016R30009)资助,在此一并致谢。
NOTES
*通讯作者。