1. 引言
传染病一直以来都是人类生存的头号大敌,不仅危害着人们的身体健康而且影响社会的稳定。近代以来,人类在科技和医药技术方面取得了巨大的进步,但一些传染病仍然对我们的生命安全产生巨大威胁,如禽流感、甲型H1N1流感以及寨卡病毒(Zika Virus)等。因此,弄清传染病的传播机制,怎样有效地预防和控制疾病的传播成为了科学研究的焦点问题。
众所周知,数学建模是研究传染病传播机制的有效手段之一。有关这方面的研究最早可追溯到上世纪初。早在1906年,Hamer在研究麻疹时构建并分析了一个离散时间模型 [1]。随后在1926年,Kermack和McKendrick在研究黑死病以及瘟疫的传播规律时,建立了易感态–感染态–移除态(susceptible-infectious-recovered, SIR)仓室模型,之后在1932年,又构建了易感态–感染态–易感态(susceptible-infectious-susceptible, SIS)传染病模型并提出了揭示传染病传播规律的“阈值定理” [2] [3] ,这些成果至今仍然被广泛的应用并且得到了蓬勃发展。但是由于传统仓室模型过于理想化,将人群看作均匀混合的,忽略了个体之间接触的异质性。随着复杂网络理论兴起和不断发展,上述不足有了更好的解决方法。复杂网络为描述社会、经济和生物等系统的拓扑结构提供了一个强有力的框架并且异质网络的度可很好地刻画接触模式的异质性 [4]。因此将复杂网络和传染病模型结合起来,研究传染病在复杂网络上的传播动力学性质成为了近些年来的研究热点 [4] [5] [6] [7] [8]。在2001年,Pastor-Satorras和Vespiganai首次基于无标度网络提出并研究了SIS传染病模型 [5] ,结果表明在有限规模网络上,传染病的传播阈值为
,而在无限规模高度异质的网络上,其传播阈值为0。Li等人在复杂网络上构建并研究了一个新的具有非线性感染率和具有出生率和死亡率的易感态–感染态–移除态–易感态(susceptible-infectious-recovered-susceptible, SIRS)模型 [6] ,Zhu等人在文献 [7] 中提出了复杂网络上的一个一般化的传染病模型,他们的结果都解释了连接异质性是如何影响传播阈值的。
然而接触模式的异质性在复杂网络中不仅表现为连边的数量不同,而且也体现在连边权重的差异上 [9]。事实上,许多常见的网络系统都是带权重的,例如交通网络、股票网络、生物网络等。在传染病传播过程中,边权可以表示两个个体之间接触的频繁程度或接触时间长短,边权越大,表示个体之间的连接越紧密,易感状态的个体被感染的几率就越大 [8] [10]。因此研究边的权重对传播过程的影响具有重要的意义。文章 [11] 利用权重来衡量个体行为对传播过程的影响,并由此估计个体的感染风险,从而采取更有效的干预措施。文章 [12] 通过边权重来表示节点之间的亲密程度,并且通过研究发现权重较大的节点更容易被感染,而对于整个网络来说,连边的权重越分散,疾病传播就会越慢。
受上述的研究成果启发,本文基于无标度网络SIRS模型,考虑感染个体的差异性,将感染个体分为低风险感染个体和高风险感染个体,并引入权重用于刻画个体之间接触的频繁程度,建立了基于权重网络的SIRS传染病模型。
2. 传染病模型
记
分别表示为t时刻度为k的易感个体的密度,低风险染病个体的密度,
高风险染病个体的密度以及康复个体的密度,其中
(n为网络的最大度)表示该节点与其他节点之间的连边数。根据异质平均场理论,可得到如下的SIRS传染病模型
(1)
其中
表示单位时间内新感染的度为k的个体密度,
代表新的感染个体为低风险感染个体的比率。
分别表示低风险染病个体,高风险染病个体的治愈率。
为康复个体的免疫丧失率。
表示为一个易感个体被一个感染的邻居节点感染的概率,并且
(2)
其中
是度为k的节点连向度为i的节点的概率。在度不相关的网络中 [13] ,
。
分别表示度为k的低风险感染,高风险感染节点的感染力,
代表度为i的节点到度为k的节点之间的感染率。
是网络中节点的度分布且
。
则为网络的平均度。对于一般的函数
,记
。
对疾病传播而言,权重用来表示传染病传播的强弱程度,因此可以用节点的度来表示连边的权重,若度为i和j的两个节点相连,那么它们之间的权重可以用一个关于i, j的函数
来表示 [14] [15] [16]。
其一般表达式为
。因为度越大,表示节点影响力越大,权重也会越大,所以
是一个关于k的增函数。函数
表示的是连边之间的权重,类似的也可建立有关节点的权重表达式 [8] :设
表示度为k的节点的权重,代表所有与它相连的边的权重之和,故
,并且在度不相关网络上,有
。
设度为i的节点有一个固定的传播率
,并且通过一条从度为i的节点到度为k的节点的连边的传播概率可由这条边的权重占节点权重的比例表示 [8] ,由此可得到感染率的表达式
(3)
将(3)代入(2),得
(4)
然后将(4)代(1),得到如下系统
(5)
其中
,且
,
。记
,则有
,即总的个体数是常数,因此不妨设
。且系统(5)的初始条件具有如下形式:
由于
,因而系统(5)等价于如下系统:
(6)
因此只需在区域
上研究系统(6)即可,并且容易验证
是关于系统(6)的正不变集。
3. 动力学分析
在这一部分,我们将讨论模型(6)的一些动力学性质。
定理1 设基本再生数
考虑系统(6),我们有如下结论:
(i) 系统(6)总存在一个无病平衡点
。
(ii) 当
时,系统(6)有且仅有唯一的正平衡点
。并且
满足
其中
。
证明:显然,
总是系统(6)的一个平衡点。我们接下来研究
的存在性。注意到平衡点
应该满足如下的方程
(7)
由方程组(7)的第一个和第二个方程,我们有
(8)
由方程组(7)的第三个方程以及等式(8)有
(9)
将等式(8)和(9)代入(3)的第一个方程,可得
(10)
将(8)和(10)式代入
的表达式,得到一个关于
的自洽方程
(11)
令
,然后方程(11)可写成如下
形式
(12)
由于
其中
。若
,则有
。此时方程(12)只存在唯一一个非零解
。即当
时,系统(6)只存在唯一的地方病平衡点。证毕。
接下来,我们将讨论(6)的无病平衡点
稳定性。
定理2 若
,系统(6)的无病平衡点
是全局渐近稳定的。
证明:令
将系统(6)可写成如下矩阵向量的形式:
(13)
其中
。
。其中O是n阶零矩阵,I是n
阶单位矩阵,而
由于向量
每一项都是非正的,因此有
,故可得如下比较系统
(14)
系统(14)只有一个平衡点
,其雅可比矩阵对应的特征方程为
其中
,
。显然
,并且
时,
,
此时A的所有特征值实部都为负的,故系统(14)的平衡点
是全局渐近稳定的。又因为矩阵A的所有非对角线上元素是非负的,因此系统(14)是拟单调增的 [17] ,故由比较原理和解的正性,定理2得证。
下面,我们来讨论系统(6)的持久性。首先,我们给出如下定义
定义 若对于系统(6)的满足初值条件
的任意解,存在一个常数
使得
则称该系统是准持久的。
然后,再引入如下引理
引理3 [4] 考虑如下n维的系统
(15)
其中,向量
,A是一个
阶方阵并且向量
在区域
内是连续可微的。假设
(i):紧的凸集
是(15)的正向不变集,并且
;
(ii):存在某个正整数
,使得
;
(iii):存在
和
的一个正的特征值对应的一个实特征向量
使得对任意的
,都有
;
(iv):对所有的
,都有
。然后,系统(15)的任何一个初值为
的解
满足
其中
不依赖于
,另外(15) 存在一个常数解
。
因此我们可得到如下定理
定理4 若
,则系统(6)是准持久的。
证明:下面我们通过引理3来证明此定理
1):紧的凸集
是(6)的正向不变集,并且
,故条件(i)成立;
2):取正整数
,易得
,因而条件(ii)成立;
3):记
,则
是一个
不可约的矩阵,且当
时,
。由文献 [18] 的引理4,
存在一个正的特征向量
,对应的特征值为
。令
,取
,因此有
,即
是矩阵
的特征向量,对应着特征值
。记
,故对所有的
,都有
,因此条件(iii)成立。
4):由于
的每一项都小于等于0,而
,故对所有的
,都有
。即条件(iv)也成立。因此,由引理3,存在常数
使得
即有
因此,定理4得证。
4. 数值模拟
这一节,我们通过两个数值仿真例子来验证相关结果的正确性。首先,根据优先连接算法我们构建了一个带有100节点的BA无标度网络。接下来我们验证
的全局稳定渐近稳定性。
例1. 这里我们取
,
以及
其它参数分别为
,
,
,
,
,
,
和
。那么,
,由定理2可知,如果
,则无病平衡点
是全局渐近稳定的。给定初值条件
,
,
和
,我们可以得到
,
,
以及
的随时间的演化图,如图1所示。从图中可以看出疾病最终都会消亡,与我们的结果相吻合。
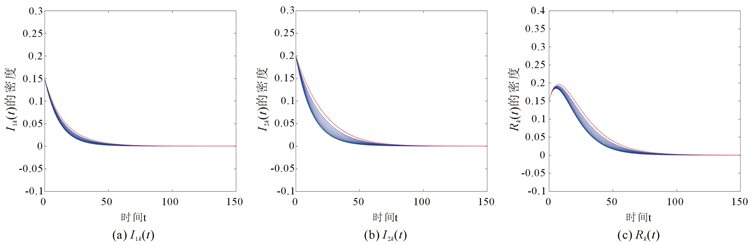
Figure 1. The time evolution of the densities of
,
and
图1.
、
以及
的时间演化图
接下来,我们验证定理1和定理4。
例2. 这里我们分别取
,
和
,其它参数及初值条件分别和例1中的相同。则有
,由前面的研究结果可知,如果
,则系统(6)存在唯一的地方病平衡点
,并且系统(6)是持久存在的
,
,
以及
的随时间的演化图,如图2所示。从图中可以看出系统最终是持久存在的,这与我们的结果是一致的。
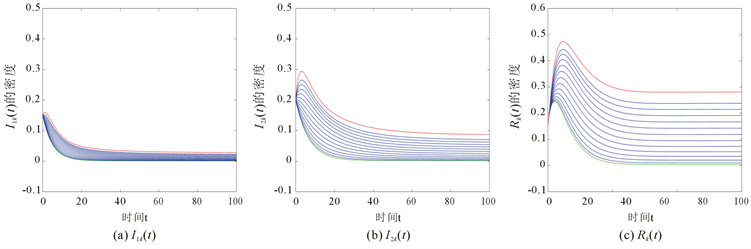
Figure 2. The time evolution of the densities of
,
and
图2.
、
以及
的时间演化图
5. 结论
为了获得个体接触的频繁程度对疾病传播的影响,我们建立并分析了一个考虑权重的SIRS网络传染病模型,得到了基本再生数,给出了地方病平衡点的存在唯一性条件以及证明了无病平衡点的全局渐近稳定性。同时还研究了系统的持久性并通过数值模拟验证了我们的结果。由前面的研究结果
可知感染者中低风险感染者所占的比率
能影响疾病传
播阈值并且还发现
随着治愈率
和
的增大而减小。因此提高疾病的治愈率是抑制疾病传播的重要措施。同时我们可以看出
对于网络拓扑结构是敏感的,网络的度和权重的改变都能导致基本再生数
的变化,进而影响疾病的传播。
基金资助
受湖南省大学生研究性学习与创新性实验计划项目(湘教通[2016] 283号(序号207))和长沙理工大学“十三五”专业综合改革试点项目(数学与应用数学专业)资助。
NOTES
*通讯作者。