ABC算法在MA(q)模型参数估计中的应用

Application of ABC Algorithm in Parameter Estimation of MA(q) Model

摘要: 本文利用近似贝叶斯计算给出了MA(q)模型的参数估计。在近似贝叶斯计算中，提高算法的抽样效率在于选取低维的包含参数信息尽可能多的统计量。在白噪声方差已知的情况下，本文采用前q阶样本自相关函数作为统计量。通过数值模拟进行比较，选用样本自相关函数远好于样本自协方差函数，大大提升了抽样的效率。在白噪声方差未知的情况下，采用前q阶样本自相关函数与样本方差作为统计量，分两步对参数进行近似贝叶斯估计。从数值模拟的效果来看，该方法大大提高了估计的精确度。

Abstract: In this paper, we provide the parameter estimation of the MA(q) model by using the approximate Bayesian computation. In the approximate Bayesian computation, a way to improve the sampling efficiency of the algorithm is choosing the statistics of low dimension, which contains as much in-formation of parameters as possible. As the variance of white noise is known, we use the sample autocorrelation function of the first q order as the statistics. Through the numerical simulations and comparison, effects of choosing the sample auto-correlation functions are much better than the sample auto-covariance function, which greatly improves the sampling efficiency. When the variance of white noise is unknown, we use the sample autocorrelation function of the first q order and the sample variance as statistics to realize a two-step approximation Bayesian parameter es-timation method. As a result of numerical simulation, this method greatly improves the accuracy of estimation.

1. 引言

时间序列MA(q)模型常见的参数估计方法为极大似然估计，对于该估计常用的数值方法有格点搜索、最陡爬坡法、Newton-Raphson方法和Davidon-Fletcher-Powell方法等，这些数值方法在高阶情况下计算过程较为复杂。在贝叶斯统计的框架下，利用MCMC方法对参数的后验分布抽样进行参数估计是近年来一种流行的方法 [1] [2] 。但无论是极大似然估计还是MCMC方法都要涉及对似然函数的计算，当样本量很大和阶数较高时，会增加计算的复杂性和计算量。本文采用操作简单又易于实现的近似贝叶斯计算(Approximate Bayesian Computation)来估计MA(q)模型的参数。

近似贝叶斯计算(简称ABC)是利用拒绝法对参数的近似后验分布进行抽样，从而给出参数估计的一种算法 [3] 。1984年由Rubin首次给出近似贝叶斯基本思想 [4] ，1997年Tavare等学者首次把该算法应用在DNA数据的统计推断中 [5] ，1999年Pritchard等学者对该算法加以推广 [6] ，并利用推广的ABC算法研究了人类Y染色体的变异。自2002年尤其是近些年来，近似贝叶斯计算作为一种复杂模型参数估计的方法广泛应用于种群遗传学 [7] 、系统生物学、流行病学和系统地理学等多个领域。提高ABC算法的抽样效率在于选取低维的参数充分统计量。在复杂模型中，找到参数的充分统计量一般是很难做到的，常见的做法是选取低维的包含参数信息尽可能多的统计量。Jean-Michel Marin等学者在文献 [8] 中利用ABC方法对MA(q)模型参数进行了估计。该文献假设模型的白噪声方差是已知的，把前q阶样本自协方差函数作为参数的统计量对后验分布进行抽样和参数估计。本文采用前q阶样本自相关函数作为参数统计量，通过数值模拟比较，选用样本自相关函数作为统计量大大提升了抽样的效率。此外，本文在白噪声方差未知的情况下，提出用前q阶样本自相关函数与样本方差作为参数的统计量，采用两步估计法，即先估计模型系数，再估计白噪声方差的ABC算法对模型参数进行估计。从数值模拟的效果来看，该方法大大提高了估计的精确度。

2. MA(q)模型

定义1：设 $\left\{x_k:k=0,\pm 1,\pm 2,\cdots \right\}$ 为一时间序列，如果

$x_k=\mu +u_k-{\theta }_1{u}_{k-1}-{\theta }_2{u}_{k-2}-\cdots -{\theta }_q{u}_{k-q},k=0,\pm 1,\pm 2,\cdots$

则称该时间序列为q阶移动平均模型，简记为MA(q)，其中 ${\theta }_q\ne 0,\theta =\left\{{\theta }_1,{\theta }_2,\cdots ,{\theta }_q\right\}$ 称为模型系数， $\left\{u_k:k=0,\pm 1,\pm 2,\cdots \right\}$ 为高斯白噪声序列，且 $u_k~N\left(0,{\sigma }^2\right)$ ， ${\sigma }^2$ 称为白噪声方差。当 $\mu =0$ 时，称序列为

中心化的MA(q)模型。对于非中心化的MA(q)模型只需做简单平移 $y_t=x_t-\mu$ 即可转化为中心化MA(q)模型。而这种转化不会影响序列之间的相关关系，因此本文只讨论中心化的MA(q)模型，即满足下面结构的模型

$x_k=u_k-{\theta }_1{u}_{k-1}-{\theta }_2{u}_{k-2}-\cdots -{\theta }_q{u}_{k-q},k=0,\pm 1,\pm 2,\cdots$

令

$\Theta \left(x\right)=1-{\theta }_{1}x-{\theta }_2{x}^2-\cdots -{\theta }_q{x}^q$

如果没有特殊说明，MA(q)模型都是指中心化的模型。称 $\Theta \left(x\right)=0$ 为模型MA(q)的特征方程。如果 $\Theta \left(x\right)=0$ 的根在单位圆外，则模型MA(q)可逆。

命题1模型MA(q)的特征方程 $\Theta \left(x\right)=0$ 根在单位圆外当且仅当该模型可逆。

命题2MA(q)模型的自相关系数 ${\rho }_k$ 与 ${\theta }_i\left(1\le i\le q\right)$ 之间具有如下的关系：

${\rho }_k=\{\begin{array}{l}1,k=0\\ \frac{-{\theta }_k+{\displaystyle \underset{i-1}{\overset{q-k}{\sum }}{\theta }_i{\theta }_{k+i}}}{1+{\theta }_1^2+\cdots +{\theta }_q^2},1\le k\le q\\ 0,k>q\end{array}$

命题1和命题2都是众所周知的性质，这里不再给出证明。

命题3若MA(q)过程可逆，则模型系数 $\theta$ 满足： $\left|{\theta }_i\right|<C_q^i,i=1,2,\cdots ,q$ 。

证：令特征多项式

$\Theta \left(x\right)=1-{\theta }_{1}x-{\theta }_2{x}^2-\cdots -{\theta }_q{x}^q=\left(1-{\lambda }_{1}x\right)\left(1-{\lambda }_{2}x\right)\left(1-{\lambda }_{3}x\right)\cdots \left(1-{\lambda }_{q}x\right)$

上面式子的右边项展开得

$1-\left({\displaystyle \underset{i=1}{\overset{q}{\sum }}{\lambda }_i}\right)x+\left({\displaystyle \underset{i<j}{\sum }{\lambda }_i{\lambda }_j}\right)x^2-\left({\displaystyle \underset{i<j<k}{\sum }{\lambda }_i{\lambda }_j{\lambda }_k}\right)x^3+\cdots +{\left(-1\right)}^q\left({\displaystyle \underset{i=1}{\overset{q}{\prod }}{\lambda }_i}\right)x^q,$

与左边式子相比较得，

${\theta }_1={\displaystyle \underset{i=1}{\overset{q}{\sum }}{\lambda }_i},{\theta }_2=-{\displaystyle \underset{i<j}{\sum }{\lambda }_i{\lambda }_j},{\theta }_3={\displaystyle \underset{i<j<k}{\sum }{\lambda }_i{\lambda }_j{\lambda }_k},\cdots ,{\theta }_q={\left(-1\right)}^q\left({\displaystyle \underset{i=1}{\overset{q}{\prod }}{\lambda }_i}\right)$

由MA(q)过程可逆可知，方程的根 ${\theta }_i=\frac{1}{{\lambda }_i}$ 在单位圆外， $i=1,2,\cdots q$ ，因此 $\left|{\lambda }_i\right|<1,i=1,2,\cdots ,q$ 。因此 $\left|{\theta }_1\right|<q=C_q^1,\left|{\theta }_2\right|<C_q^2,\left|{\theta }_3\right|<C_q^3,\cdots ,\left|{\theta }_q\right|<C_q^q$ ，即 $\left|{\theta }_i\right|<C_q^i\left(1\le i\le q\right)$ 。

3. 近似贝叶斯计算(ABC)

为了便于说明近似贝叶斯计算方法，首先介绍一下贝叶斯模型。假设 $X={\left(X_1,X_2,\cdots ,X_n\right)}^{\text{T}}$ 的密度 $p_{X|\theta }\left(x|\theta \right)$ ，其中 $\theta$ 为模型的参数， $x={\left(x_1,x_2,\cdots ,x_n\right)}^{\text{T}}$ 。 $\theta$ 的先验密度为 $p_{\theta }\left(\theta \right)$ ，则在 $X=x$ 的条件下， $\theta$

的后验密度为

$p_{\theta |X}\left(\theta |x\right)=\frac{p_{X|\theta }\left(x|\theta \right)p_{\theta }\left(\theta \right)}{{\displaystyle \int p_{X|\theta }\left(x|t\right)p_{\theta }\left(t\right)\text{d}t}}$

从上面公式可以看出，对于后验密度的计算，需要涉及到似然函数 $p_{X|\theta }\left(x|\theta \right)$ 以及 ${\displaystyle \int p_{X|\theta }\left(x|t\right)p_{\theta }\left(t\right)\text{d}t}$

的计算。在复杂的模型中，这是十分困难的事情。近似贝叶斯计算可以避开这两个问题的计算。下面我们给出简单的介绍。

近似贝叶斯计算，简称ABC，是一种近似后验分布的抽样模拟方法。该方法最显著的特点就是容易

实现，不需要计算似然函数 $p_{X|\theta }\left(x|\theta \right)$ 。一般来说当模型比较复杂的时候，似然函数以及后验密度很难进

行计算，不会有一个具体的表达式。为了估计复杂统计模型的参数，可以利用ABC算法模拟后验样本，用这些样本替代似然函数的计算，从而得到模型参数的估计。

我们首先给出基本的ABC算法。

算法1基本ABC算法

输入：样本数据 $x^{*}\in R^n$ ； $\theta$ 的先验分布 $p_{\theta }(\cdot )$ ；似然函数 $p_{X|\theta }\left(\cdot |\theta \right)$ ； $R^n$ 的距离 $\rho \left(\cdot ,\cdot \right)$ ；容忍度 $\delta >0$ 。

输出：近似后验分布 $p_{\theta |X}\left(\theta |x^{*}\right)$ 的样本 ${\theta }_1,{\theta }_2,\cdots ,{\theta }_n$ 。

算法步骤：

for $i=1$ to n do

repeat

根据先验分布 $p_{\theta }(\cdot )$ 生成 ${\theta }^{\prime }$

根据似然函数 $p_{X|\theta }\left(\cdot |{\theta }^{\prime }\right)$ 生成x

until $\rho \left(x,x^{*}\right)\le \delta$

${\theta }_i={\theta }^{\prime }$

end for

基本ABC算法的缺点是当维数n比较大时， $\theta$ 被拒绝的概率就很高，这样计算成本就会大大增加。为此我们选用参数 $\theta$ 的低维充分统计量 $S\left(x\right)\in R^d$ 替代x (其中 $d\ll n$ )，即下面改进的ABC算法。

算法2改进的ABC算法

输入：样本数据 $x^{*}\in R^n$ ； $\theta$ 的先验分布 $p_{\theta }(\cdot )$ ；似然函数 $p_{X|\theta }\left(\cdot |\theta \right)$ ； $R^d$ 的距离 $d\left(\cdot ,\cdot \right)$ ；容忍度 $\delta >0$ 。

输出：近似后验分布 $p_{\theta |X}\left(\theta |x^{*}\right)$ 的样本 ${\theta }_1,{\theta }_2,\cdots ,{\theta }_n$ 。

算法步骤：

for $i=1$ to n do

repeat

根据先验分布 $p_{\theta }(\cdot )$ 生产 ${\theta }^{\prime }$

根据似然函数 $p_{X|\theta }\left(\cdot |{\theta }^{\prime }\right)$ 生产x

until $d\left(S\left(x\right),S\left(x^{*}\right)\right)\le \delta$

${\theta }_i={\theta }^{\prime }$

end for

可以证明，当 $\delta \to 0$ ，所得到的样本就是后验证分布的样本。事实上，对于复杂的模型，找到低维的充分参数统计量是十分困难，因此尽可能寻找包含参数 $\theta$ 信息尽可能的统计量。

4. MA(q)模型参数的ABC估计

令 $\left\{x_k:k=0,\pm 1,\pm 2,\cdots \right\}$ 为MA(q)模型，即

$x_k=\mu +u_k-{\theta }_1{u}_{k-1}-{\theta }_2{u}_{k-2}-\cdots -{\theta }_q{u}_{k-q},k=0,\pm 1,\pm 2,\cdots$

${\theta }_q\ne 0$ ， $\theta =\left\{{\theta }_1,{\theta }_2,\cdots ,{\theta }_q\right\}$ 称为模型系数， $\left\{u_k:k=0,\pm 1,\pm 2,\cdots \right\}$ 为高斯白噪声序列，且 $u_k~N\left(0,{\sigma }^2\right)$ ， $\sigma$ 称为白噪声标准差。

为了保证模型系数估计的唯一性，我们假设模型MA(q)可逆的。令

$D=\left\{\theta \in R^q:1-{\theta }_{1}x-{\theta }_2{x}^2-\cdots -{\theta }_q{x}^q=0的根在圆外\right\}$ 。由命题1可知，模型MA(q)可逆当且仅当模型系数 $\theta \in D$ 。本文假定 $\theta$ 的先验分布 $p_{\theta }(\cdot )$ 为D的均匀分布， $\sigma$ 的先验分布为逆伽马分布，即， $\sigma =\frac{1}{\tau }$ ， $\tau ~\Gamma \left(\alpha ,\beta \right)$ ， $\alpha ,\beta$ 为伽马分布的参数且已知， $\theta ,\tau$ 相对独立。

在ABC算法中，首先要随机生成一个服从D上的均匀分布 $\theta$ ，当 $q=1$ 时， $D=\left(0,1\right)$ ，即 $\theta ~U\left(0,1\right)$ ，当 $q=2$ 时， $D=\left\{\theta =\left({\theta }_1,{\theta }_2\right):-2<{\theta }_1<2,{\theta }_1+{\theta }_2<1,{\theta }_2-{\theta }_1<1\right\}$ 。当 $q\ge 3$ 时，

$D=\left\{\theta \in R^q:1-{\theta }_{1}x-{\theta }_2{x}^2-\cdots -{\theta }_q{x}^q=0的根在圆外\right\}$ 很难找到具体的不等式给出D的表示。根据命题3，若模型MA(q)可逆，则模型系数 $\theta \in \Delta =\left\{\theta \in R^q:\left|{\theta }_i\right|<C_q^i,i=1,2,\cdots ,q\right\}$ 。因此我们首先模拟一个服从 $\Delta$ 上的均分分布的随机向量 $\theta$ ，然后再判断 $\theta$ 是否满足 $1-{\theta }_{1}x-{\theta }_2{x}^2-\cdots -{\theta }_q{x}^q=0$ 的根再圆外。如果在圆外，

便接受它，否则拒绝它。这样便得到一个模拟服从D上均匀分布随机向量的算法：

算法3

输入：模型阶数 $q\ge 2$

输出：生成服从D上均匀分布的随机向量 $\theta$

算法步骤：

repeat

随机生成服从 $\Delta$ 上均匀分布的随机变量 ${\theta }^{\prime }$

until ${\theta }^{\prime }$ 满足： $1-{{\theta }^{\prime }}_{1}x-{{\theta }^{\prime }}_2{x}^2-\cdots -{{\theta }^{\prime }}_q{x}^q=0$ 的根在圆外

$\theta ={\theta }^{\prime }$

假设 $x=\left\{x_1,x_2,\cdots ,x_n\right\}$ 为MA(q)模型的样本数据。令 $\hat{\rho }\left(x\right)=\left({\hat{\rho }}_1\left(x\right),{\hat{\rho }}_2\left(x\right),\cdots ,{\hat{\rho }}_q\left(x\right)\right)$ 为前q阶样本自相关系数， $S\left(x\right)=\left({\hat{\gamma }}_1\left(x\right),{\hat{\gamma }}_2\left(x\right),\cdots ,{\hat{\gamma }}_q\left(x\right)\right)$ 为前q阶样本自协方差函数。文献 [8] 讨论了在白噪声序列的方差已知情况下MA(2)模型ABC的参数估计，采用的统计量为 $S\left(x\right)$ 。本文首先给出在白噪声序列的方差 ${\sigma }^2$

已知情况下MA(q)模型参数ABC估计。

算法4

输入：样本数据 $x^{*}=\left(x_1^{*},x_2^{*},\cdots ,x_n^{*}\right)$ ；模型阶数q；伽马分布的参数 $\alpha ,\beta$ ； $\theta$ 样本容量N；容忍度 $\epsilon$ ； $R^d$ 距离 $d\left(\cdot ,\cdot \right)$ ；白噪声标准差 ${\sigma }^2$ 。

输出： $\theta$ 的ABC估计 $\hat{\theta }$ 。

算法步骤：

1.计算样本 $x^{*}$ 的自相关系数 $\hat{\rho }\left(x^{*}\right)=\left({\hat{\rho }}_1^{*}\left(x\right),{\hat{\rho }}_2^{*}\left(x\right),\cdots ,{\hat{\rho }}_q^{*}\left(x\right)\right)$ ；

2.for $i=1$ to N do

repeat

利用算法3随机生成 $\theta =\left({\theta }_i:i=1,2,\cdots ,q\right)$ ；

随机生成系数为 $\theta$ ，白噪声方差 ${\sigma }^2$ 的MA(q)模型的时间序列 $x=\left(x_1,x_2,\cdots ,x_n\right)$ ，计算样本自相关系数 $\hat{\rho }\left(x\right)=\left({\hat{\rho }}_i\left(x\right),i=1,2,\cdots ,q\right)$ ；

until $d\left(S\left(x\right),S\left(x^{*}\right)\right)\le \epsilon$

${\theta }_i={\theta }^{\prime }$ end for

3.计算模型系数ABC估计 $\hat{\theta }=\frac{1}{N}{\displaystyle \underset{i=1}{\overset{N}{\sum }}{\theta }_i}$ 。

下面我们讨论在白噪声序列的方差未知情况下MA(q)模型参数的ABC估计。由命题2可知，两个可逆的MA(q)模型系数 $\theta$ 相同当且仅当它们的前q阶自相关系统相同。这说明q过程的模型系数 $\theta$ 可以由前面q阶确定，与白噪声的方差无关。因此在估计参数 $\theta$ 时，可以假设MA(q)的白噪声方差已知(不妨假定 $\sigma =1$ )，这样利用算法4给出 $\theta$ 的ABC估计 $\hat{\theta }$ ；然后再用样本方差作为统计量，给出 $\sigma$ 的ABC估计，具体算法如下：

算法5

输入：样本数据 $x^{*}=\left(x_1^{*},x_2^{*},\cdots ,x_n^{*}\right)$ ；模型阶数q；伽马分布的参数 $\alpha ,\beta$ ； $\theta$ 的样本容量N；容忍度 ${\epsilon }_1,{\epsilon }_2$ ； $R^d$ 的距离 $d\left(\cdot ,\cdot \right)$ 。

输出： $\theta ,\sigma$ 的ABC估计 $\hat{\theta },\hat{\sigma }$ 。

算法步骤：

1.计算样本 $x^{*}$ 的样本标准差 ${\sigma }^{*}$ 和自相关系数 $\hat{\rho }\left(x^{*}\right)=\left({\hat{\rho }}_1^{*}\left(x\right),{\hat{\rho }}_2^{*}\left(x\right),\cdots ,{\hat{\rho }}_q^{*}\left(x\right)\right)$ ；

2.for $i=1$ to N do

repeat

利用算法3随机生成一个 $\theta =\left({\theta }_i:i=1,2,\cdots ,q\right)$ ；

随机生成系数 $\theta$ ，白噪声标准差 $\sigma =1$ 的MA(q)模型时间序列 $x=\left(x_1,x_2,\cdots ,x_n\right)$ ，计算样本自相关系数 $\hat{\rho }\left(x\right)=\left({\hat{\rho }}_i\left(x\right),i=1,2,\cdots ,q\right)$ ；

until $d\left(\hat{\rho }\left(x\right),\hat{\rho }\left(x^{*}\right)\right)\le {\epsilon }_1$

${\theta }_i={\theta }^k$

end for

3.计算模型系数的ABC估计 $\hat{\theta }=\frac{1}{N}{\displaystyle \underset{i=1}{\overset{N}{\sum }}{\theta }_i}$ ；

4.for $i=1$ to N do

repeat

生成随机数 $\tau ~\Gamma \left(\alpha ,\beta \right)$ ，令 $\sigma =\frac{1}{\tau }$ ；

随机生成系数为 $\hat{\theta }$ ，白噪声标准差 $\sigma$ 的MA(q)模型时间序列 $x=\left\{x_1,x_2,\cdots ,x_n\right\}$ ，计算 $x=\left\{x_1,x_2,\cdots ,x_3\right\}$ 的样本标准差 $\sigma$ ；

until $\left|{\sigma }^{*}-\sigma \right|\le {\epsilon }_2$

${\sigma }_i=\sigma$

end for

5.计算白噪声标准差的ABC估计 $\hat{\sigma }=\frac{1}{N}{\displaystyle \underset{i=1}{\overset{N}{\sum }}{\sigma }_i}$ ；

5. 数值模拟

为了比较自协方差函数和自相关函数作为统计量的ABC参数估计效果，我们假定模型为

$x_k=u_k-0.6u_{k-1}-0.2u_{k-2},k=0,\pm 1,\pm 2,\cdots$

其中 $\left\{u_k\right\}$ 为高斯白噪声，且标准差为1。

首先根基模型随机生成时间序列样本 $x^{*}=\left(x_1^{*},x_2^{*},\cdots ,x_{10000}^{*}\right)$ ，然后根据给废除分别由自协方差函数和

自相关函数作为参量统计量模拟的后验样本。为了便于比较，我们没有采用在算法4中给定容忍度条件下，选取 $\theta$ 的样本，而是先生成容量100000的 $\theta$ 样本，然后按照距离由小到大进行排序，选取距离最小的前1000个作为 $\theta$ 作为后验样本。图1和图2分别为自协方差函数和自相关函数作为统计量近似后验分布的 $\theta =\left({\theta }_1,{\theta }_2\right)$ 的样本散点图。与自协方差的函数相比，由自相关函数作为统计量得到样本点更加集中在 $\theta =\left(0.6,0.2\right)$ 附近。图3和图4分别表示由自协方差函数和自相关函数对后验分布抽样的 ${\theta }_1$ 与 ${\theta }_2$ 的直方图。表1给出了自协方差函数和自相关函数作为参数统计量ABC估计的 $\theta$ 均值和方差。显然由自相关函数作为统计量得到的估计精度大大优于自协方差统计量。

下面我们给出在白噪声未知的情况下ABC估计。我们仍选用上面的MA(2)模型，这里假设白噪声的

先验分布为 $\sigma =\frac{1}{\tau },\tau ~\Gamma \left(2,5\right)$ 。首先根据模型随机生成时间序列样本 $x^{*}=\left(x_1^{*},x_2^{*},\cdots ,x_{10000}^{*}\right)$ 。然后选取容忍度 $\epsilon =0.01$ ，利用算法5模拟 $\theta =\left({\theta }_1,{\theta }_2\right)$ 的容量为1000后验样本，最后给出参数 $\theta$ 的估计。在此基础上选用选取容忍度 $\epsilon =0.01$ ，模拟 $\sigma$ 容量为1000后验样本，然后给出 $\sigma$ 的ABC估计值。为了ABC估计的

效果，我们和极大似然估计进行比较，结果见表2。

从表2可以看出，与极大似然估计相比较，ABC估计精确更高。

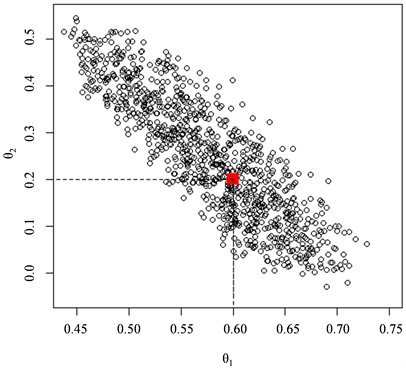
Figure 1. The posterior sample scatters with autocovariance function as statistic

图1. 自协方差函数为统计量的后验样本散点图

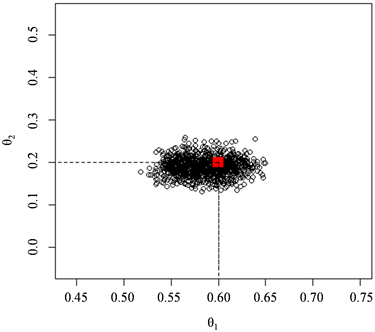
Figure 2. The posterior sample scatters with autocorrelation functions as statistics

图2. 自相关函数为统计量的后验样本散点

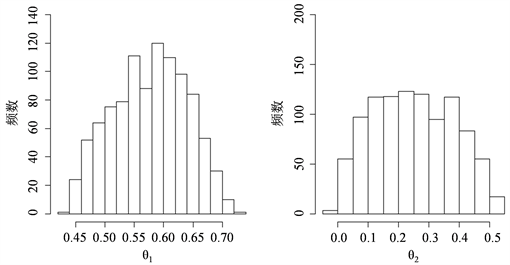
Figure 3. Histogram of sampling posterior distribution from autocovariance function

图3. 由自协方差函数对后验分布抽样的直方图

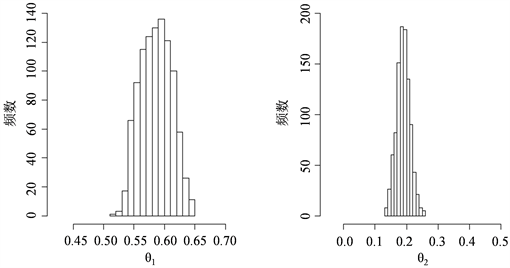
Figure 4. Histogram of sampling posterior distribution from autocorrelation function

图4. 由自相关函数对后验分布抽样的直方图

Table 1. Comparison of ABC estimation results with autocovariance function and autocorrelation function as statistics

表1. 自协方差函数和自相关函数为统计量的ABC估计结果对比

Table 2. Comparison of the maximum likelihood estimation and ABC estimation with autocorrelation function as statistic

表2. 极大似然估计和自相关函数为统计量的ABC估计对比

6. 实例分析

疾病预防控制局自2004年1月起每月定期发布全国法定传染病疫情概况，其中乙肝是目前各类病毒性肝炎中危害最严重的，也是发病数最多的一个型别，并且不像其他类型的肝炎那样呈现出明显的季节性或趋势性变化，因此对于乙肝发病数的建模比其他类型的肝炎更复杂。我们选取2004年1月至2018年6月期间的月乙肝发病人数数据进行建模，然后通过2018年7~9月数据来说说明模型的拟合效果，最后利用模型对2018年10~12月乙肝发病数做出预测。

自相关函数是识别一个MA模型阶的有用工具，图5和图6分别给出了乙肝发病数的时间序列图和样本自相关函数图。由图6可见，该序列的1阶和2阶自相关系数显著，因此选用MA(2)对时间序列数据进行建模。

Figure 5. Time series chart of the number of patients with Hepatitis B

图5. 乙肝发病人数的时间序列

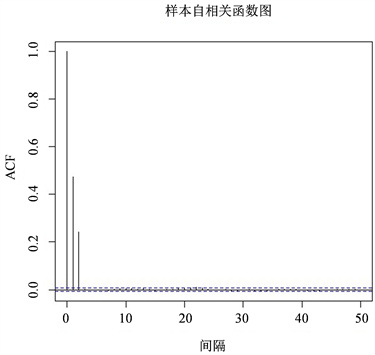
Figure 6. Autocorrelation function chart of the number of patients with Hepatitis B

图6. 乙肝发病人数样本自相关函数

MA(2)模型如下：

$x_k=c+u_k-{\theta }_1{u}_{k-1}-{\theta }_2{u}_{k-2},$

其中 ${\left(u_k\right)}_{k\in z}$ 时高斯白噪声，即 $u_i~N\left(0,{\sigma }^2\right)$ 。

显然c的估计为样本均值 $\hat{c}=99708$ 。通过算法5对参数进行ABC估计，得出 ${\theta }_1,{\theta }_2,\sigma$ 的估计值分别为：

${\hat{\theta }}_1=0.5143,{\hat{\theta }}_2=0.8455,\hat{\sigma }=2286.843$

因此该MA(2)模型为：

$y_k=99708+u_k-0.5143u_{k-1}-0.8455u_{k-2},$

其中 $u_k~N\left(0,{2286.843}^2\right)$ 。

表3分别给出2018年7，8，9三个月我国乙肝发病人数的实际值，预测值与相对误差，以及未来三个月我国乙肝发病人数的95%置信区间和预测值。

Table 3. Prediction of the number of patients with Hepatitis B in China by ABC algorithm

表3. ABC算法对我国乙肝发病人数预测结果

基金项目

浙江省自然科学基金(LQ18A010007)。

NOTES

^*通讯作者。