脉冲输注寨卡的脑癌治疗模型的动力学分析

Dynamic Analysis of the Model of Brain Cancer Treatment by Pulse Infusion of Zika

摘要: 本文利用生物数学建模的思想，构建了一个输注寨卡病毒的脑癌治疗数学模型。在没有脉冲输注的情形，得到了模型解的有界性和非负性，并且利用常微分方程稳定性理论分析了模型平衡点的稳定性和阈值 ；当考虑脉冲输注时，讨论了周期解的局部渐近稳定性，并对脉冲输注量进行了估计，最后通过数值模拟对文中的主要结论做了合理的解释。

Abstract: In this paper, we consider a bio-mathematical modeling to construct a pulse infusion of zika virus for the treatment of brain cancer. The boundedness and non-negativeness of the model are ob-tained. By means of the theory of pulse differential equation, we derive the stability and threshold of the equilibria of the model. Then, the asymptotic stability of the periodic solution under pulse condition is discussed. Finally, the pulse infusion volume of the model is estimated and numerical simulation is carried out.

1. 模型的提出

目前，科学家们发现了一些病毒攻击癌细胞的特性，将这些病毒命名成溶瘤病毒，并在此基础上研究了一些溶瘤病毒攻击癌细胞的过程，得到了一些研究结果 [1] [2] [3] [4]。下面，在前人研究的基础上探究溶瘤病毒寨卡和脑癌之间的反应过程。

脑癌是严重威胁人类健康的疾病，传统的放疗和化疗在杀死脑癌细胞的同时，对人体正常细胞也会造成伤害。生长于颅内的肿瘤通称为脑瘤，包括由脑实质发生的原发性脑瘤和由身体其他部位转移至颅内的继发性脑瘤。原发性脑瘤依其生物特性又分良性和恶性。良性脑瘤生长缓慢，包膜较完整，不浸润周围组织及分化良好；恶性脑瘤生长较快，无包膜，界限不明显，呈浸润性生长，分化不良。无论良性或恶性，均能挤压、推移正常脑组织，造成颅内压升高，威胁人的生命 [5] [6]。美国圣路易斯华盛顿大学和加州大学圣地亚哥分校的一项新研究称，寨卡病毒能够针对性地杀死脑癌中的干细胞，其与常规治疗手段结合，有一天可能成为治疗致命脑癌—胶质母细胞瘤的一种有效手段 [6]。

寨卡病毒(Zika Virus)属黄病毒科(Flaviviridae)黄病毒属(Flavivirus)，呈球形，直径约为40~70 nm，有包膜。基因组为单股正链RNA，长度约为10.8 Kb，可分为亚洲型和非洲型两个基因型。寨卡病毒病是由寨卡病毒引起的一种自限性急性传染病，主要通过蚊虫叮咬传播，也可以通过性传播，最早于1947年在乌干达被发现，但直到2015年在南美大规模爆发流行，导致胎儿小头症发病率急剧上升，才引起广泛关注。

2001年，Wodarz在Cancer research上发表了一篇关于病毒缓解肿瘤增长的文章。该文章基于病毒能够感染肿瘤细胞然而对于正常细胞无害这一思想建立了三个常微分方程(ODE)模型 [7] [8]。这些模型分别对应于三种不同的治疗机制，这里仅列举第一个模型。该模型只考虑病毒毒素对肿瘤具有杀灭作用，而关于病毒毒素产生的CTL反应可以清理感染病毒的肿瘤细胞，具体方程如下表示：

$\{\begin{array}{l}\frac{\text{d}x}{\text{d}t}=rx\left(1-\frac{x+y}{k}\right)-dx-\beta xy\hfill \\ \frac{\text{d}y}{\text{d}t}=\beta xy+sy\left(1-\frac{x+y}{k}\right)-ay-pyz\hfill \\ \frac{\text{d}z}{\text{d}t}=qyz-bz\hfill \end{array}$ (1)

其中 $x,y,z$ 分别表示未感染病毒的肿瘤细胞个数，感染病毒的肿瘤细胞个数，以及对于病毒抗原的CTL反应个数，d为未感染细胞的死亡率， $\beta$ 表示病毒在肿瘤中的传播能力(或者简单的认为病毒的复制能力)，感染的细胞被病毒杀死的能力为a，病毒CTL对于抗原扩张率为q，且以b的比率衰减，p表示免疫细胞捕杀肿瘤病毒的能力。假设未感染病毒的肿瘤细胞x与感染病毒的肿瘤细胞y均符合logistic增长，CTL增值反应正比于感染病毒的肿瘤细胞个数y，以及CTL个数z。

受到上述启发以及文献 [6] 的实验结果，我们假设寨卡在患有脑癌的宿主体内的扩散与侵入过程如下：在成人宿主体内，寨卡病毒不会感染非癌性脑细胞，它只会优先靶向脑癌干细胞，抑制其增殖和扩散，使其丧失自我更新能力。与此同时，它也会受到机体免疫细胞的攻击(称为病毒特异性CTL反应)。根据文献 [6] [8] ，我们考虑感染病毒的肿瘤细胞不继续增长繁殖，且忽略病毒在细胞间游走的过程，同时假设未受感染的脑癌细胞的增长符合logistic增长模型。因此，未受寨卡感染的脑癌细胞，寨卡病毒颗粒数与病毒特异性免疫细胞之间的关系结构图如下(如图1所示)：

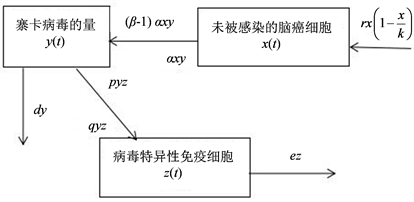
Figure 1. Diagram of the relationship between Zika, brain cancer cells and immune response

图1. 寨卡、脑癌细胞、免疫反应之间的关系图

图1所示的是寨卡病毒与脑癌细胞在宿主体内的进行过程，这里不考虑感染寨卡病毒的脑癌细胞的增长繁殖。因此，根据 $x,y,z$ 之间的相互关系，建立相应的微分方程模型如下：

$\{\begin{array}{l}\frac{\text{d}x}{\text{d}t}=rx\left(1-\frac{x}{k}\right)-\alpha xy,\hfill \\ \frac{\text{d}y}{\text{d}t}=\left(\beta -1\right)\alpha xy-dy-pyz,\hfill \\ \frac{\text{d}z}{\text{d}t}=qyz-ez,\hfill \end{array}$ (2)

其中x表示未受寨卡感染的脑癌细胞，y表示寨卡病毒颗粒数，z表示病毒特异性免疫细胞，其余参数的意义见表1。

在实际的治疗过程中，需要对宿主体内定期输注寨卡病毒，因此有必要考虑如下带有脉冲输注的数学模型：

$\{\begin{array}{l}\begin{array}{l}\frac{\text{d}x}{\text{d}t}=rx\left(1-\frac{x}{k}\right)-\alpha xy,\hfill \\ \frac{\text{d}y}{\text{d}t}=\left(\beta -1\right)\alpha xy-dy-pyz\hfill \\ \frac{\text{d}z}{\text{d}t}=qyz-ez,\hfill \end{array},t\ne nT,\hfill \\ \Delta y\left(t\right)=\bar{y},t=nT,n=1,2,3,\cdots ,\hfill \end{array}$ (3)

其中， $y\left(t\right)$ 在脉冲时刻是左连续的，即 $y\left(t^{-}\right)=\underset{h\to 0^{+}}{\lim }y\left(t-h\right)=y\left(t\right)$ ，而脉冲条件为： $\Delta y\left(t\right)=y\left(t^{+}\right)-y\left(t\right)=\bar{y}$ ，所以 $y\left(t^{+}\right)=y\left(t\right)+\bar{y}$ 。T为脉冲输注寨卡病毒的周期( $T>0$ )， $\bar{y}$ 则表示在 $t=nT$ ( $n\in N_{+}$ )时刻向宿主输注的寨卡病毒量( $\bar{y}$ 是一个正的常数)。

Table 1. Parameters in Model (2) and (3)

表1. 模型(2)和(3)的参数

全文默认， $r>0,k>0,\alpha >0,\beta >0,d>0,p>0,q>0,e>0$ 。

本文的主要结论是：当不考虑脉冲输注时，寨卡病毒将被病毒特异性免疫细胞消灭，最终脑癌细胞

仍然存在，即脑癌是无法得到根治的；当考虑脉冲输注，并且脉冲输注量为 $\bar{y}\in \left(\frac{rdT}{\alpha },\frac{edT}{q}\right)$ 时，系统(3)的T-周期解 $E_3=\left(0,\tilde{y}\left(t\right),0\right)$ 是局部渐近稳定的，即在适当时间间隔内输注适量的寨卡病毒，脑癌是可以

得到有效控制的。所以我们认为考虑脉冲作用的影响可为脑癌临床治疗策略的制定提供具有参考价值的帮助。

2. 没有脉冲输注的情形

下面我们将讨论没有脉冲输注时，模型(2)的动力学性态。

令 $R_{+}=\left[0,\infty \right)$ ， $R_{+}^3=\left\{\left(x,y,z\right)\in R^3:x>0,y>0,z>0\right\}$ ， $f=\left(f_1,f_2,f_3\right)$ 表示系统(2)的右端映射， $X:R_{+}\to R^3$ 表示系统(2)的解。显然，系统(2)的解 $X\left(t\right)$ 在 $R_{+}$ 是连续可微的，并且 $f=\left(f_1,f_2,f_3\right)$ 的光滑

性保证了系统(2)解的全局存在性和唯一性。由系统(2)知下面引理是显然成立的。

引理1：设是系统(2)的过初值 $\left(x_0,y_0,z_0\right)\in R_{+}^3$ 的解，那么对所有 $t\ge 0$ ，都有 $x\left(t\right)\ge 0$ ， $y\left(t\right)\ge 0$ ， $z\left(t\right)\ge 0$ [9]。

从现实生物意义的角度考虑，我们假设系统(2)的初始条件满足：

$x\left(0\right)>0,y\left(0\right)>0,z\left(0\right)>0.$

定理1：设 $x\left(t\right),y\left(t\right),z\left(t\right)$ 为系统(2)满足初始条件 $x\left(0\right)>0,y\left(0\right)>0,z\left(0\right)>0$ 的解，则当 $t\ge 0$ 时，有 $x\left(t\right)>0,y\left(t\right)>0,z\left(t\right)>0$ ，并且存在正数 $M_1,M_2,M_3$ ，使得对于任意的 $t>0$ ， $x\left(t\right)\le M_1,y\left(t\right)\le M_2,z\left(t\right)\le M_3$ 。

证明：由解的存在唯一性以及初值条件易知，当 $t\ge 0$ 时，必有 $x\left(t\right)>0,y\left(t\right)>0,z\left(t\right)>0$ 。下面证明

系统(2)解的有界性。考虑到系统(2)的非负性，定义：

$G\left(t\right)=x\left(t\right)+\frac{1}{\beta -1}y\left(t\right)+\frac{p}{q\left(\beta -1\right)}z\left(t\right),\delta =\min \left\{r,d,e\right\}.$

上述函数对时间t求导得，

$\frac{\text{d}G\left(t\right)}{\text{d}t}=\frac{\text{d}x}{\text{d}t}+\frac{1}{\beta -1}\frac{\text{d}y}{\text{d}t}+\frac{p}{q\left(\beta -1\right)}\frac{\text{d}z}{\text{d}t}=rx\left(1-\frac{x}{k}\right)-\frac{d}{\beta -1}y-\frac{pe}{q\left(\beta -1\right)}z\le rk-\delta G\left(t\right).$

从而有，

$\underset{t\to \infty }{\lim }\left[x\left(t\right)+\frac{1}{\beta -1}y\left(t\right)+\frac{p}{q\left(\beta -1\right)}z\left(t\right)\right]\le \frac{rk}{\delta }$ .

由解的非负性知，系统(2)的解 $x\left(t\right),y\left(t\right),z\left(t\right)$ 是有界的。

下面研究系统(2)的平衡点和阈值。令系统(2)的右边等于0，我们有，

$\{\begin{array}{l}rx\left(1-\frac{x}{k}\right)-\alpha xy=0,\\ \left(\beta -1\right)\alpha xy-dy-pyz=0,\\ qyz-ez=0.\end{array}$ (4)

不难发现，当不存在寨卡病毒时，系统存在两个平衡点：平凡平衡点 $E_0=\left(0,0,0\right)$ ，以及原始脑癌平衡点 $E_1=\left(k,0,0\right)$ (没有寨卡病毒，就没有病毒特异性免疫反应，也就没有相应的免疫细胞)。

按照传染病学中基本再生数 ${\Re }_0$ 的计算方法计算 [8] [9] [11] ，可以求得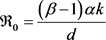。下面的结论

表明： ${\Re }_0$ 是寨卡病毒能否在脑癌细胞内传播的阈值。容易求得系统(2)的其他两个平衡点为：治疗平衡点

$E_2=\left(\frac{d}{\left(\beta -1\right)\alpha },\frac{r}{\alpha }\left[1-\frac{d}{\left(\beta -1\right)k\alpha }\right],0\right)$

和特异性免疫反应平衡点

$E_3=\left(k\left(1-\frac{e\alpha }{qr}\right),\frac{e}{q},\frac{d}{p}\left[\left(1-\frac{e\alpha }{qr}\right){\Re }_0-1\right]\right).$

记 $R_1=1+\frac{ek\left(\beta -1\right){\alpha }^2}{qdr}$ 。下面分情况进行具体分析。

1) 当 ${\Re }_0\le 1$ 时，系统(2)存在唯一的原始脑癌平衡点 $E_1=\left(k,0,0\right)$ ，相应脑癌细胞的浓度达到最大值。此时没有输注寨卡病毒。

2) 当 $1<{\Re }_0\le R_1$ 时，系统(2)存在治疗平衡点 $E_2$ ，此时，寨卡病毒能够在脑癌细胞内传播，寨卡病毒治疗机制开始产生。

3) 当 ${\Re }_0>R_1$ 时，系统(2)还存在一个内部平衡点——特异性免疫反应平衡点 $E_3$ ，此时，未感染寨卡的脑癌细胞，寨卡病毒和病毒特异性免疫细胞三者均存在。

为研究系统(2)平衡点的局部稳定性，计算系统在点 $E=\left(x,y,z\right)$ 的雅可比矩阵 $J\left(E\right)$ ，

$J\left(E\right)=\left(\begin{array}{ccc}r\left(1-\frac{x}{k}\right)-\frac{rx}{k}-\alpha y& -\alpha & 0\\ \left(\beta -1\right)\alpha y& \left(\beta -1\right)\alpha x-d-pz& -py\\ 0& qz& qy-e\end{array}\right).$ (5)

定理2：平凡平衡点 $E_0=\left(0,0,0\right)$ 总是不稳定的；当 ${\Re }_0\le 1$ 时，原始脑癌平衡点 $E_1=\left(k,0,0\right)$ 是全局渐近稳定的。

证明：由 $J\left(E\right)$ 可知，

$J\left(E_1\right)=\left(\begin{array}{ccc}-r& -\alpha k& 0\\ 0& \left(\beta -1\right)\alpha k-d& 0\\ 0& 0& -e\end{array}\right).$ (6)

$J\left(E_1\right)$ 的特征方程是，

$\det \left(\lambda I-J\left(E_1\right)\right)=\left(\lambda +r\right)\left(\lambda +e\right)\left[\lambda +d-\left(\beta -1\right)\alpha k\right]=0$ . (7)

易知当 ${\Re }_0=\frac{\left(\beta -1\right)\alpha k}{d}<1$ 时，(7)的所有特征根都是负实数，因此由Roth-Hurwitz判据可知 $E_1=\left(k,0,0\right)$ 是局部渐近稳定的。同理可得，平衡点 $E_0=\left(0,0,0\right)$ 所对应的特征根为， ${\lambda }_1=r,{\lambda }_2=-d,{\lambda }_3=-e$ 。因此平凡平衡点 $E_0=\left(0,0,0\right)$ 总是不稳定的。

下证当 ${\Re }_0\le 1$ 时， $E_1=\left(k,0,0\right)$ 是全局渐近稳定的。定义Lyapunov函数

$V_1\left(x,y,z\right)=x-x_1-x_1\ln \frac{x}{x_1}+\frac{y}{\beta -1}+\frac{p}{q\left(\beta -1\right)}z.$

对Lyapunov函数 $V_1\left(x,y,z\right)$ 沿系统(2)的轨线求导得，这里 $x_1=k$ ，

$\begin{array}{c}\frac{\text{d}{V}_1}{\text{d}t}=\left(1-\frac{x_1}{x}\right)\frac{\text{d}x}{\text{d}t}+\frac{1}{\beta -1}\frac{\text{d}y}{\text{d}t}+\frac{p}{q\left(\beta -1\right)}\frac{\text{d}z}{\text{d}t}\\ =\left(1-\frac{x_1}{x}\right)\left[rx\left(1-\frac{x}{k}\right)-\alpha xy\right]+\frac{p}{q\left(\beta -1\right)}\left(qyz-ez\right)+\frac{1}{\beta -1}\left[\left(\beta -1\right)\alpha xy-dy-pyz\right]\\ =\frac{-r\left(x-x_1\right)\left(x-k\right)}{k}+\alpha x_{1}y-\frac{d}{\beta -1}y-\frac{pe}{q\left(\beta -1\right)}z\\ =-\frac{r}{k}{\left(x-k\right)}^2+\frac{d}{\beta -1}\left({\Re }_0-1\right)y-\frac{pe}{q\left(\beta -1\right)}z\le 0.\end{array}$ (8)

由于 ${\Re }_0\le 1$ 时，有 $\frac{\text{d}{V}_1}{\text{d}t}\le 0$ 且 $\frac{\text{d}{V}_1}{\text{d}t}=0$ 当且仅当 $x\left(t\right)=k,y\left(t\right)=0,z\left(t\right)=0$ 。所以 $\left\{\left(x,y,z\right)\in R_{+}^3|\frac{\text{d}{V}_1}{\text{d}t}=0\right\}$ 的最大不变集是一个单点集 $E_1$ 。由LaSalle不变集原理 [9] ，可知当 ${\Re }_0\le 1$ 时，原始脑癌平衡点 $E_1=\left(k,0,0\right)$

是全局渐近稳定的。

定理3：当 $1<{\Re }_0\le R_1$ 时， $E_2$ 是全局渐近稳定的；而当 ${\Re }_0>R_1$ 时， $E_2$ 是不稳定的。

证明：由 $J\left(E\right)$ 可知，

$J\left(E_2\right)=\left(\begin{array}{ccc}\frac{-dr}{k\alpha \left(\beta -1\right)}& \frac{-d}{\beta -1}& 0\\ r\left(\beta -1\right)-\frac{dr}{k\alpha }& 0& \frac{pdr}{k\left(\beta -1\right){\alpha }^2}-\frac{pr}{\alpha }\\ 0& 0& \frac{qr}{\alpha }-\frac{qdr}{k\left(\beta -1\right){\alpha }^2}-e\end{array}\right).$ (9)

则 $J\left(E_2\right)$ 的特征方程为，

$\det \left(\lambda I-J\left(E_2\right)\right)=\left(\lambda -\frac{qr}{\alpha }+\frac{qdr}{k\left(\beta -1\right){\alpha }^2}+e\right)\left[\lambda \left(\lambda +\frac{dr}{k\alpha \left(\beta -1\right)}\right)+dr-\frac{r{d}^2}{k\alpha \left(\beta -1\right)}\right]=0.$

化简，得：

$\left[\lambda -e\left(\frac{qdr}{ek\left(\beta -1\right){\alpha }^2}\left({\Re }_0-1\right)-1\right)\right]\left[{\lambda }^2+\frac{dr\lambda }{k\alpha \left(\beta -1\right)}+\frac{r{d}^2}{k\alpha \left(\beta -1\right)}\left({\Re }_0-1\right)\right]=0.$ (10)

显然有当 $1<{\Re }_0<R_1$ 时，有 $\frac{qdr}{ek\left(\beta -1\right){\alpha }^2}\left({\Re }_0-1\right)-1<0$ ，故特征方程(10)左边第一个因式对应的特征根为负实数。又因为特征方程左边第二个因式是二次函数， $\frac{dr}{k\alpha \left(\beta -1\right)}>0$ ， $\frac{r{d}^2}{k\alpha \left(\beta -1\right)}\left({\Re }_0-1\right)>0$ 。由二次函数的性质可得，该二次函数的零点都具有负实部。因此当 $1<{\Re }_0<R_1$ 时， $E_2$ 是局部渐近稳定的。而当 ${\Re }_0>R_1$ 时，有 $\frac{qdr}{ek\left(\beta -1\right){\alpha }^2}\left({\Re }_0-1\right)-1>0$ ，从而存在一个正的特征根，因此当 ${\Re }_0>R_1$ 时， $E_2$ 是不稳定的。

下证当 $1<{\Re }_0\le R_1$ 时， $E_2$ 是全局渐近稳定的。定义Lyapunov函数

$V_2\left(x,y,z\right)=x-x_2-x_2\ln \frac{x}{x_2}+\frac{1}{\beta -1}\left[y-y_2-y_2\ln \frac{y}{y_2}\right]+\frac{p}{q\left(\beta -1\right)}z$ .

这里 $x_2=\frac{d}{\left(\beta -1\right)\alpha },y_2=\frac{r}{\alpha }-\frac{dr}{\left(\beta -1\right)k{\alpha }^2}$ 。对Lyapunov函数 $V_2\left(x,y,z\right)$ 沿系统(2)的轨线求导得，

$\begin{array}{c}\frac{\text{d}{V}_2}{\text{d}t}=\left(1-\frac{x_2}{x}\right)\frac{\text{d}x}{\text{d}t}+\frac{1}{\beta -1}\left(1-\frac{y_2}{y}\right)\frac{\text{d}y}{\text{d}t}+\frac{p}{q\left(\beta -1\right)}\frac{\text{d}z}{\text{d}t}\\ =\left(x-x_2\right)\left[r\left(1-\frac{x}{k}\right)-\alpha y\right]+\frac{pz}{q\left(\beta -1\right)}\left(qy-e\right)+\frac{1}{\beta -1}\left(y-y_2\right)\left[\left(\beta -1\right)\alpha x-d-pz\right]\\ =\left(x-x_2\right)\left[r-\frac{rx}{k}-\alpha y-\left(r-\frac{r{x}_2}{k}-\alpha y_2\right)\right]+\frac{pz}{q\left(\beta -1\right)}\left[qy-e-\left(q{y}_2-e\right)\right]\\ +\frac{1}{\beta -1}\left(y-y_2\right)\left\{\left(\beta -1\right)\alpha x-d-pz-\left[\left(\beta -1\right)\alpha x_2-d-p{z}_2\right]\right\}\end{array}$

$\begin{array}{l}=\left(x-x_2\right)\left[-\frac{r}{k}\left(x-x_2\right)-\alpha \left(y-y_2\right)\right]+\frac{pz}{\beta -1}\left(y-y_2\right)\\ +\frac{1}{\beta -1}\left(y-y_2\right)\left[\left(\beta -1\right)\alpha \left(x-x_2\right)-pz\right]\\ =-\frac{r}{k}{\left(x-x_2\right)}^2\le 0\end{array}$ (11)

由于当 $1<{\Re }_0\le R_1$ 时，(11)中 $\frac{\text{d}{V}_2}{\text{d}t}\le 0$ ，且 $\frac{\text{d}{V}_2}{\text{d}t}=0$ 当且仅当 $x=x_2$ 。又由LaSalle不变集原理，可知边界平衡点 $E_2$ 是全局渐近稳定的。

定理4：当 ${\Re }_0>R_1$ 时，特异性免疫反应平衡点 $E_3$ 是全局渐近稳定的。

证明：定义Lyapunov函数

$V_3\left(x,y,z\right)=x-x_3-x_3\ln \frac{x}{x_3}+\frac{1}{\beta -1}\left[y-y_3-y_3\ln \frac{y}{y_3}\right]+\frac{p}{q\left(\beta -1\right)}\left[z-z_3-z_3\ln \frac{z}{z_3}\right]$ .

这里 $x_3=k-\frac{ek\alpha }{qr},y_3=\frac{e}{q},z_3=\frac{d}{p}\left[\left(1-\frac{e\alpha }{qr}\right){\Re }_0-1\right]$ 。对Lyapunov函数 $V_3\left(x,y,z\right)$ 沿系统(2)的轨线求导得，

$\begin{array}{c}\frac{\text{d}{V}_3}{\text{d}t}=\left(1-\frac{x_3}{x}\right)\frac{\text{d}x}{\text{d}t}+\frac{1}{\beta -1}\left(1-\frac{y_3}{y}\right)\frac{\text{d}y}{\text{d}t}+\frac{p}{q\left(\beta -1\right)}\left(1-\frac{z_3}{z}\right)\frac{\text{d}z}{\text{d}t}\\ =\left(x-x_3\right)\left[r\left(1-\frac{x}{k}\right)-\alpha y\right]+\frac{p}{q\left(\beta -1\right)}\left(qy-e\right)\left(z-z_3\right)\\ +\frac{1}{\beta -1}\left(y-y_3\right)\left[\left(\beta -1\right)\alpha x-d-pz\right]\\ =-\frac{r\left(x-x_3\right)\left(x-k\right)}{k}-\alpha y\left(x-x_3\right)+\frac{p}{q\left(\beta -1\right)}\left(q{y}_3-e\right)\left(z-z_3\right)\\ +\frac{1}{\beta -1}\left(y-y_3\right)\left[\left(\beta -1\right)\alpha x-d\right]-\frac{p{z}_3}{\beta -1}\left(y-y_3\right)\end{array}$

$\begin{array}{l}=-\frac{r}{k}{\left(x-x_3\right)}^2-\frac{r}{k}\left(x_3-k\right)\left(x-x_3\right)-\alpha y\left(x-x_3\right)+\alpha x\left(y-y_3\right)\\ -\frac{d}{\beta -1}\left(y-y_3\right)-\frac{p{z}_3}{\beta -1}\left(y-y_3\right)\\ =-\frac{r}{k}{\left(x-x_3\right)}^2+\left(x-x_3\right)\left[r\left(1-\frac{x_3}{k}\right)-\alpha y_3\right]+\left(\alpha x_3-\frac{d}{\beta -1}\right)\left(y-y_3\right)-\frac{p{z}_3}{\beta -1}\left(y-y_3\right)\\ =-\frac{r}{k}{\left(x-x_3\right)}^2+0+\frac{y-y_3}{\beta -1}\left[\left(\beta -1\right)\alpha x_3-d-p{z}_3\right]\\ =-\frac{r}{k}{\left(x-x_3\right)}^2\le 0\end{array}$ (12)

由于当 $1<{\Re }_0\le R_1$ 时，(12)中 $\frac{\text{d}{V}_3}{\text{d}t}<0$ ，且 $\frac{\text{d}{V}_3}{\text{d}t}=0$ 当且仅当 $x=x_2$ 。又由LaSalle不变集原理，可知特异性免疫反应平衡点 $E_3$ 是全局渐近稳定的。

上述结论表明，无论哪一种情况， $\underset{t\to \infty }{\lim }{x}_1\left(t\right)\ne 0$ ，也就是说，脑癌细胞的数量不会趋于零，从而达不到好的治疗效果。因此，仅一次输注寨病毒，不能有效根除癌细胞。下面我们考虑定期输注寨卡病毒，即脉冲输注的情况。

3. 脉冲输注模型的动力学行为

系统(3)的解是逐段连续的函数 $X:R_{+}\to R_{+}^3$ ， $X\left(t\right)$ 在 $\left(nT,\left(n+1\right)T\right],n\in Z_{+}$ 上是连续的，且 $\underset{t\to n{T}^{+}}{\lim }X\left(t\right)=X\left(n{T}^{+}\right)$ 存在。函数 $f=\left(f_1,f_2,f_3\right)$ 表示系统(3)的右端映射，它的光滑性保证了系统(3)解的存

在性和唯一性 [10] [11]。

为了求系统(3)的周期解，这里我们令 $z\left(t\right)=0$ ，系统(3)简化为，

$\{\begin{array}{l}\begin{array}{l}\frac{\text{d}x}{\text{d}t}=rx\left(1-\frac{x}{k}\right)-\alpha xy,\hfill \\ \frac{\text{d}y}{\text{d}t}=\left(\beta -1\right)\alpha xy-dy,t\ne nT,\hfill \end{array}\hfill \\ \Delta y\left(t\right)=\bar{y},t=nT,n=1,2,3,\cdots .\hfill \end{array}$ (13)

类似于文献 [11] 的讨论，应用脉冲微分方程的比较定理，先来考虑比较系统，

$\{\begin{array}{l}\frac{\text{d}y}{\text{d}t}=-dy,t\ne nT\hfill \\ \Delta y\left(t\right)=y\left(t^{+}\right)-y\left(t\right)=\bar{y},t=nT\hfill \end{array}$ (14)

系统(14)在区间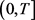的以 $y\left(0^{+}\right)=y_0$ 为初值的解为： $y\left(t\right)=y_0{\text{e}}^{-dt}$ ；在区间 $\left(T,2T\right]$ 的解为 $y\left(t\right)=y\left(T^{+}\right){\text{e}}^{-d\left(t-T\right)}=y_0{\text{e}}^{-dt}+\bar{y}{\text{e}}^{-d\left(t-T\right)}$ ；一般地，系统(14)在区间 $\left(\left(n-1\right)T,nT\right],n\in Z_{+}$ 的解为：

$y\left(\left(n+1\right)T^{+}\right)=f\left(y\left(n{T}^{+}\right)\right)=\left[y\left(n{T}^{+}\right)+\bar{y}\right]{\text{e}}^{-dT}.$

设 $F:y\left(n{T}^{+}\right)\to y\left(\left(n+1\right)T^{+}\right)$ 是一个频闪映射，满足方程

$y\left(\left(n+1\right)T^{+}\right)=f\left(y\left(n{T}^{+}\right)\right)=\left[y\left(n{T}^{+}\right)+\bar{y}\right]{\text{e}}^{-dT}.$

该映射有唯一的不动点， $y^{*}=\frac{\bar{y}}{1-{\text{e}}^{-dT}}$ 。在(14)中取初值条件 $y\left(0^{+}\right)=y^{*}$ ，容易得到

$\tilde{y}\left(t\right)=y^{*}{\text{e}}^{-d\left(t-nT\right)}=\frac{\bar{y}{\text{e}}^{-d\left(t-nT\right)}}{1-{\text{e}}^{-dT}},\left(nT<t\le \left(n+1\right)T,n\in Z_{+},\tilde{y}\left(0^{+}\right)=y^{*}=\frac{\bar{y}}{1-{\text{e}}^{-dT}}\right).$

是系统(14)的一个正周期解，而系统(14)以 $y\left(0^{+}\right)=y_0\ge 0$ 为初值的解为： $y\left(t\right)=\left[y_0-y^{*}\right]{\text{e}}^{-dt}+\tilde{y}\left(t\right)$ ， $t\in \left(nT,\left(n+1\right)T\right],n\in Z_{+}$ 。于是得到下面结论。

引理2：系统(14)存在一个正周期解 $\tilde{y}\left(t\right)$ ，并且当 $t\to \infty$ 时，它的任意解 $y\left(t\right)$ 满足： $\underset{t\to \infty }{\lim }\left|y\left(t\right)-\tilde{y}\left(t\right)\right|=0$ 。

因此，系统(3)有一个无特异性免疫反应，且正常脑癌细胞为0的T-周期解为：

$E_3=\left(0,\tilde{y}\left(t\right),0\right)=\left(0,\frac{\bar{y}{\text{e}}^{-d\left(t-nT\right)}}{1-e^{-dT}},0\right),nT<t\le \left(n+1\right)T,n\in Z_{+}.$

下面我们考虑T-周期解 $E_3=\left(0,\tilde{y}\left(t\right),0\right)$ 的局部稳定性。

定理5：假设 $\frac{r}{\alpha }<\frac{e}{q}$ ，则当 $\bar{y}\in \left(\frac{rdT}{\alpha },\frac{edT}{q}\right)$ 时，系统(3)的T-周期解 $E_3=\left(0,\tilde{y}\left(t\right),0\right)$ 是局部渐近稳定的。

证明：设 $\left(x\left(t\right),y\left(t\right),z\left(t\right)\right)$ 是系统(3)的任意解。作变换令 $x\left(t\right)=X\left(t\right)$ ， $$ ， $z\left(t\right)=Z\left(t\right)$ ，并将其代入系统(3)后，将新得到的系统在点 $\left(0,0,0\right)$ 处线性化，得到系统(3)在T-周期解 $E_3=\left(0,\tilde{y}\left(t\right),0\right)$ 处

的线性化系统为：

$\{\begin{array}{l}\frac{\text{d}X}{\text{d}t}=\left(r-\alpha \tilde{y}\left(t\right)\right)X，\\ \frac{\text{d}Y}{\text{d}t}=\left(\beta -1\right)\alpha \tilde{y}\left(t\right)X-dY-p\tilde{y}\left(t\right)Z,\\ \frac{\text{d}Z}{\text{d}t}=\left(q\tilde{y}\left(t\right)-e\right)Z.\end{array}$ (15)

考虑系统(15)满足初始条件 $X\left(0\right)=x_0,Y\left(0\right)=y_0,Z\left(0\right)=z_0$ 的解 $\left(X\left(t\right),Y\left(t\right),Z\left(t\right)\right)$ 。

由 $\tilde{y}\left(t\right)=y^{*}{\text{e}}^{-d\left(t-nT\right)}=\frac{\bar{y}{\text{e}}^{-d\left(t-nT\right)}}{1-{\text{e}}^{-dT}}$ ， $t\in \left(nT,\left(n+1\right)T\right],n\in Z_{+}$ ，容易求得：

$X\left(t\right)=x_0\exp \left[{\displaystyle {\int }_0^t\left(r-\alpha \tilde{y}\left(s\right)\right)\text{d}s}\right]=x_0\exp \left[rt\text{+}\frac{\alpha \bar{y}}{d\left(1-{\text{e}}^{-dT}\right)}\left({\text{e}}^{-dt}-1\right)\right],t\in \left[0,T\right].$

同理可求得：

$Z\left(t\right)=z_0\exp \left[{\displaystyle {\int }_0^t\left(q\tilde{y}\left(s\right)-e\right)\text{d}s}\right]=z_0\exp \left[-\frac{q\bar{y}}{d\left(1-{\text{e}}^{-dT}\right)}\left({\text{e}}^{-dt}-1\right)-et\right],t\in \left[0,T\right].$

所以可得：

$Y\left(t\right)={\text{e}}^{-dt}\left({\displaystyle {\int }_0^t\left[\left(\beta -1\right)\alpha X\left(s\right)-pZ\left(s\right)\right]\tilde{y}\left(s\right){\text{e}}^{ds}\text{d}s}+y_0\right).$ (16)

令 $\left(x_0,y_0,z_0\right)$ 分别为 $\left(1,0,0\right),\left(0,1,0\right),\left(0,0,1\right)$ ，可得解 $\left(X_i\left(t\right),Y_i\left(t\right),Z_i\left(t\right)\right),i=1,2,3$ 。

从而，求得系统(15)的基解矩阵 $\Phi \left(t\right)$ 为：

$\Phi \left(t\right)=\left(\begin{array}{ccc}{X}^{*}\left(t\right)& 0& 0\\ P\left(t\right)& Y^{*}\left(t\right)& Q\left(t\right)\\ 0& 0& Z^{*}\left(t\right)\end{array}\right),t\in \left[0,T\right].$

其中，

$X^{*}\left(t\right)=\exp \left[rt+\frac{\alpha \bar{y}}{d\left(1-{\text{e}}^{-dT}\right)}\left({\text{e}}^{-dt}-1\right)\right],$

$Y^{*}\left(t\right)={\text{e}}^{-dt},$

$Z^{*}\left(t\right)=\exp \left[-et+\frac{q\bar{y}}{d\left(1-{\text{e}}^{-dT}\right)}\left(1-{\text{e}}^{-dt}\right)\right],$

$P\left(t\right)=\left(\beta -1\right)\alpha {\text{e}}^{-dt}{\displaystyle {\int }_0^t{X}^{*}\left(s\right)\tilde{y}\left(s\right){\text{e}}^{ds}\text{d}s},Q\left(t\right)=-p{\text{e}}^{-dt}{\displaystyle {\int }_0^t{Z}^{*}\left(s\right)\tilde{y}\left(s\right){\text{e}}^{ds}\text{d}s}.$

显然，

$\left(\begin{array}{ccc}{X}_1\left(0\right)& X_2\left(0\right)& X_3\left(0\right)\\ Y_1\left(0\right)& Y_2\left(0\right)& Y_3\left(0\right)\\ Z_1\left(0\right)& Z_2\left(0\right)& Z_3\left(0\right)\end{array}\right)=\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right).$

于是系统(15)的单值矩阵为：

$M=\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right)\Phi \left(T\right)=\Phi \left(T\right)=\left(\begin{array}{ccc}\exp \left[rT-\frac{\alpha \bar{y}}{d}\right]& 0& 0\\ \Delta & {\text{e}}^{-dT}& \Delta \\ 0& 0& \exp \left[-eT+\frac{q\bar{y}}{d}\right]\end{array}\right).$

系统(15)的3个Floquet乘子分别为：

${\lambda }_1=\text{exp}\left[rT-\frac{\alpha \bar{y}}{d}\right],{\lambda }_3=\exp \left[-eT+\frac{q\bar{y}}{d}\right],{\lambda }_2={\text{e}}^{-dT}.$

显然，当 $\bar{y}\in \left(\frac{rdT}{\alpha },\frac{edT}{q}\right)$ 时， $0<{\lambda }_1<1,0<{\lambda }_2<1,0<{\lambda }_3<1$ ，此时系统(3)的T-周期解 $E_3=\left(0,\tilde{y}\left(t\right),0\right)$

是局部渐近稳定的。

4. 脉冲输注量估计

由定理5得，系统(15)的3个Floquent乘子(矩阵M的特征值)分别为：

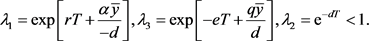
显然，当 ${\lambda }_1<1,{\lambda }_3<1$ 时，系统(3)的T-周期解 $E_3=\left(0,\tilde{y}\left(t\right),0\right)$ 是局部渐近稳定的。

此时，

$rT+\frac{\alpha \bar{y}}{-d}<0,-eT+\frac{q\bar{y}}{d}<0,$

解得：

$\frac{rdT}{\alpha }<\bar{y}<\frac{edT}{q},\left(\frac{r}{\alpha }<\frac{e}{q}\right),\frac{q\bar{y}}{de}<T<\frac{\alpha \bar{y}}{rd}.$

即 $T\in \left(\frac{q\bar{y}}{de},\frac{\alpha \bar{y}}{rd}\right),\left(\frac{r}{\alpha }<\frac{e}{q}\right)$ 时，系统(3)的T-周期解 $E_3=\left(0,\tilde{y}\left(t\right),0\right)$ 是局部渐近稳定的。

5. 数值模拟、总结

为了说明所得到的结论能否从一个量化的角度给予解释，在本节中，我们利用了数学软件Matlab求系统(3)的数值解 [12]。通过图像观察系统(3)的动力学稳定性性态，来验证前面所得到的理论结果。图2给出了系统(3)的数值例子，其中参数： $r=0.8,k=20,\alpha =0.6,\beta =2,d=0.5,p=0.4,q=0.4,e=0.8$ ，这里仅供参考。(初始条件为： $x\left(0\right)=1.6,y\left(0\right)=0.1,z\left(0\right)=0.08$ )这里，我们分别取满足定理5条件的四组数值： $T=2,\bar{y}=1$ ， $T=0.5,\bar{y}=1$ ， $T=0.5,\bar{y}=4$ ， $T=4,\bar{y}=4$ ，得到系统(3)的解曲线，分别见图3，图4，图5，图6。

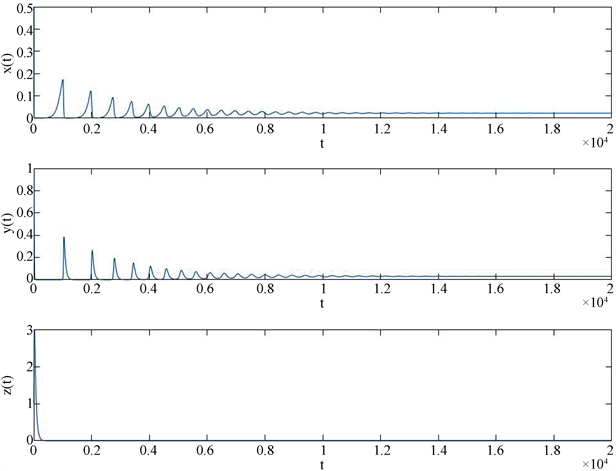
Figure 2. Change in solution (2) of the system without pulse effect

图2. 没有脉冲效应时系统(2)解的变化

Figure 3. When the pulse period and zika infusion amount are respectively $T=2,\bar{y}=1$ , the solution curve of system (2)

图3. 当脉冲周期和寨卡输注量分别为 $T=2,\bar{y}=1$ 时，系统(2)的解曲线

Figure 4. When the pulse period and zika infusion amount are respectively $T=0.5,\bar{y}=1$ , the solution curve of system (2)

图4. 当脉冲周期和寨卡输注量分别为 $T=0.5,\bar{y}=1$ 时，系统(2)的解曲线

Figure 5. When the pulse period and zika infusion amount are respectively $T=0.5,\bar{y}=4$ , the solution curve of system (2)

图5. 当脉冲周期和寨卡输注量分别为 $T=0.5,\bar{y}=4$ 时，系统(2)的解曲线

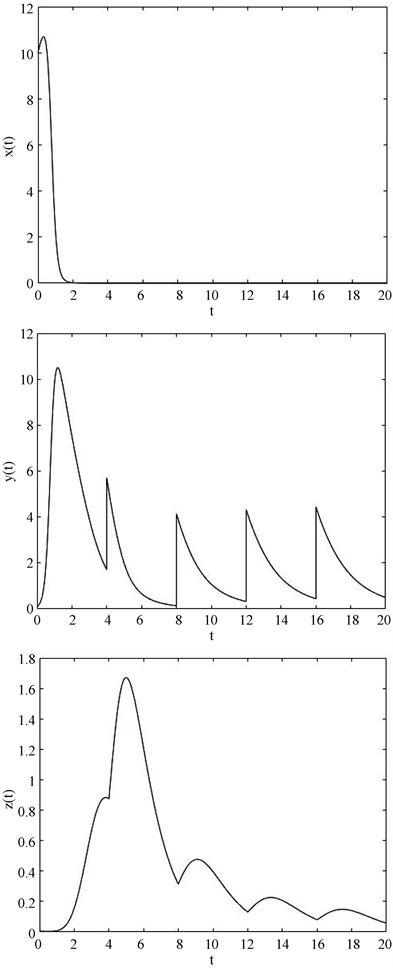
Figure 6. When the pulse period and zika infusion amount are respectively $T=4,\bar{y}=4$ , the solution curve of system (2)

图6. 当脉冲周期和寨卡输注量分别为 $T=4,\bar{y}=4$ 时，系统(2)的解曲线

数值模拟结果显示：由图2所示，系统(2)中，当没有脉冲条件时，寨卡病毒和脑癌干细胞最终将趋于平衡，病毒特异性免疫细胞被消灭，机体免疫系统被破坏，达不到所要的结果。其次，图3，图4，图5，图6都验证了系统(3)的T-周期解 $E_3=\left(0,\tilde{y}\left(t\right),0\right)$ 的局部渐近稳定性。图3与图4相比较及图5与图6相比较，说明每次输注的寨卡病毒量相同，但脉冲周期长度不同时，对脑癌细胞的影响几乎相同，但对特异性免疫细胞的影响则不同，周期长度越长，寨卡病毒量越少，对应的免疫细胞会越少，但最终都会趋于一个稳定的值；最后，图4与图5相比较，说明当脉冲周期相同，而寨卡输注量不同时，特异性免疫细胞受到的影响不大，寨卡病毒对脑癌细胞的杀伤程度会有所增加，且输注的寨卡量越大，免疫细胞刚开始增长的速度较快，但后来趋于平缓状态，对脑癌细胞的清除速率也越大，最终都将趋于稳定状态。

总结：本章比较了有无脉冲输注寨卡病毒的情况下，模型平衡点和脉冲周期解的稳定性。结果表明：当没有脉冲条件时，寨卡病毒将被病毒特异性免疫细胞消灭，最终脑癌干细胞还是存在，即脑癌是无法

得到根治的；当脉冲输注量为： $\bar{y}\in \left(\frac{rdT}{\alpha },\frac{edT}{q}\right),\left(\frac{r}{\alpha }<\frac{e}{q}\right)$ 时，系统(3)的T-周期解 $E_3=\left(0,\tilde{y}\left(t\right),0\right)$ 是局部

渐近稳定的，即在适当时间间隔内输注适量的寨卡病毒，脑癌是可以得到有效控制的。所以我们认为考虑脉冲作用的影响可为脑癌临床治疗策略的制定提供具有参考价值的帮助。

致谢

本文得到国家自然科学基金(11771104)资助，在此表示感谢！

NOTES

^*通讯作者。