1. 引言
近年来,新型材料的不断发展和研究,各种材料力学性能的研究也日益重要。准确地获得各种力学性能的本构关系,是设计和优化各种工程结构的基础和前提,自1949年Kolsky首次提出分离式霍普金森杆(split Hopkinson pressure bar,简称SHPB)以来,SHPB技术应用范围越来越广,尤其是脆性材料力学特性的研究。由于技术的限制,环境的影响,实验需多次进行,而SHPB实验过程的数值模拟,特别是在加载阶段的模拟,成为重要的过程和手段,数值模拟过程可以更好地为实际实验中的力学性能分析提供良好的参考价值。
在国内,李为民研究了较大直径的分离式霍普金森杆的应力均匀和恒应变率加载试验技术 [1] ;冯明德等人对SHPB实验技术的某些问题进行了研究 [2] [3] ;张柱等人主要研究了脆性混凝土模拟过程中的弥散效应、应力均匀和径向惯性效应等问题 [4] ;王鲁明等人主要研究了脆性材料在SHPB实验过程中的测试问题 [5] ;学者对岩石力学性能测试做了主要研究 [6] [7] [8] [9] ,为研究岩石在冲击荷载下的力学响应取得重大突破,奠定了岩石力学性能测试的基础;宋力,胡时胜等人主要研究了均匀性问题、恒应变率和数据处理手段 [10] [11] [12] ,SHPB实验技术得以成功的前提在于其两个假定和数据处理的准确性。
本文通过ANSYS软件对SHPB实验过程中不同速度子弹入射进行力学性能仿真计算,与标准性能对照,研究试件的应力–应变曲线,利用ANSYS软件对SHPB实验进行模拟验证,并通过变化网格划分方法观察数值模拟对精确度的影响。
2. SHPB实验
2.1. 实验概况
如图1所示,将一个弹性杆分成两个部分,利用子弹或炸药爆炸产生冲击,而试件则夹在输入杆与输出杆之间,并在末尾加上阻尼装置,直接利用应变片测试,通过二次计算,用这种方法测出试件的应力-应变曲线。
2.2. SHPB实验的两个假定
1) 一维应力波假定:假设应力脉冲在杆中是无畸变的线弹性应力波。由于入射波的波长和入射杆的直径相比较,要大许多。因此试验中可忽略杆的横向振动,即试样满足一维应力的条件。此时我们可以忽略杆中应力波传播的弥散效应,即只存在轴向应力,我们可以认为,在波导杆中间部位的信息,可以代替波导杆与试件接触处的信息,根据一维应力波理论从而求出试件的应力–应变曲线。
设入射应变脉冲
沿着杆的传播方向为正,那么反射脉冲
沿着杆的负向传播,则输入杆与试件的交界面
处的轴向位移
可表示为:
(2.1)
其中,
为波导杆的弹性纵波波速(查资料可知,在钢中该值约为5000 m/s)。
同理,透射杆与试件交界处
处的轴向位移
可由投射应变脉冲
得到:
(2.2)
中间材料的平均应变
为:
(2.3)
试件的应变率
为:
(2.4)
其中
为试件的原始长度。
根据一维应力波的理论,入射杆与试件接触面
处的轴力为:
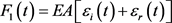 (2.5)
(2.5)
试件与透射杆接触面
处的轴力为:
 (2.6)
(2.6)
中间材料中的平均应力为:
(2.7)
为试件的截面面积,
入射方轴力,
透射方轴力,E试件弹性模量,
试件平均应变。
2) 均匀性假定:我们认为,当在界面处产生反射波以及在界面处产生透射波,分别向入射杆和透射杆传播的过程中,应力波也同时在试件内部在两个界面中间不停的往返传播。可以考虑当试件无限小时,试件内部沿杆方向的应力/应变分布将逐渐趋于均匀化。这样,在实验过程中可以忽略试件的应力波效应。这就是SHPB实验技术能够成立的第二个假定——均匀性假定。
由均匀性假定,根据一维应力波原理可得:
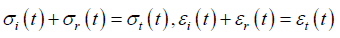 (2.8)
(2.8)
则有入射波、反射波和透射波可得试件的应力、应变和应变率,如果只采用入射波和透射波可得:
(2.9)
一般运用两波法与三波法进行运算。
3. SHPB实验过程的数值模拟
3.1. 有限元模型
数值模型的尺寸及材料参数,见表1~表3。

Table 1. Device and specimen dimensions
表1. 装置及试件尺寸

Table 2. Bullets, incident rods, transmission rod materials
表2. 子弹、入射杆、透射杆材料

Table 3. Materials of the test piece
表3. 试件的材料
本文主要选取了3DSOLID164单元模型。该单元采用线性函数单元,是8节点六面单元体。依照材料尺寸进行建模,如图2。LS-DYNA的接触类型主要有结点约束法、分配参数法和对称罚函数法。本文采用最后一种方法,即对称罚函数法。这是因为对称罚函数法原理简单,编程容易,很少激起沙漏效应,且算法动态守恒准确。因此,对称罚函数法在LS-DYNA被广泛应用。SHPB数值模型图如图3 (红色为子弹,蓝色为入射杆,绿色为试件,黄色为透射杆)。

Figure 3. SPHB rod numerical model diagram
图3. SPHB杆数值模型图
3.2. 模拟结果对比与分析
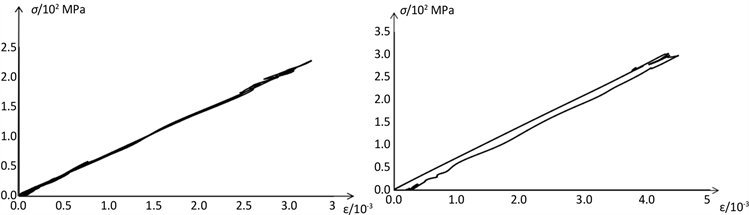
通过后处理软件LS-PREPOST就可以直接得出入射杆和透射杆的应力–时间曲线。本文通过不同的入射速度进行对照。分为10 m/s、15 m/s、20 m/s,分别得到相应的反射与透射波形图,且通过两个波形图利用一维应力波原理,数值计算所得,计算方法为第2章两个假定中的二波法和三波法得到试件的应力-应变曲线。见图4。
 (a) 10 m/s (b) 15 m/s
(a) 10 m/s (b) 15 m/s (c) 20 m/s
(c) 20 m/s
Figure 4. Stress-strain curve of the test piece
图4. 试件应力–应变曲线
由图4(a)、图4(b)当子弹速度为10 m/s和15 m/s时,由于试件受到的应力较小,因此在实验过程中仍然处于弹性变形阶段,其应力–应变曲线为线性曲线,其斜率为其弹性模量。由图4(c)分析可知,当速度为20 m/s时,在子弹的冲击下,试件所受到的应力超出弹性阶段,随着应变的增大,应力先是处于弹性阶段,随应变线性增加,随后进入屈服阶段和塑性变形阶段,试件产生较大变形,图满足弹塑性材料的应力–应变曲线,但是由于实验误差,曲线存在误差和实验所得曲线存在微小误差。
3.3. 网格划分对应力波传播过程的影响
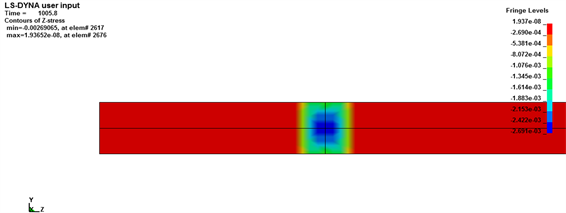
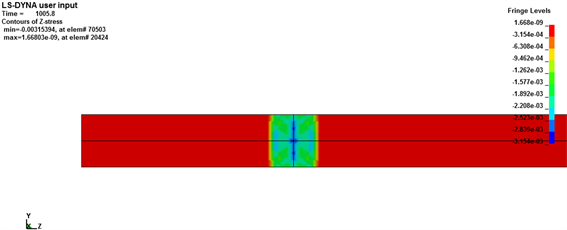
在子弹冲击过程中,网格划分的选择会对波导杆中应力波的传播产生影响,本文中主要选取以单位单元,1/2单元,1/3单元划分网格时,研究在10 m/s速度冲击下,分别在接触后8 μs与45 μs时刻,应力波的传播,探究网格划分的大小对应力波传播的影响。单位单元见图5,1/2单位单元见图6,1/3单位单元见图7。
 (a)
(a) (b)
(b)
Figure 5. Stress diagram of unit cell meshing; (a) After contact 8 μs; (b) After contact 45 μs
图5. 单位单元网格划分时应力图;(a) 接触后8 μs;(b) 接触后45 μs
 (a)
(a) (b)
(b)
Figure 6. Stress diagram for 1/2 unit cell meshing; (a) After contact 8 μs; (b) After contact 45 μs
图6. 1/2单位单元网格划分时应力图;(a) 接触后8 μs;(b) 接触后45 μs
 (a)
(a)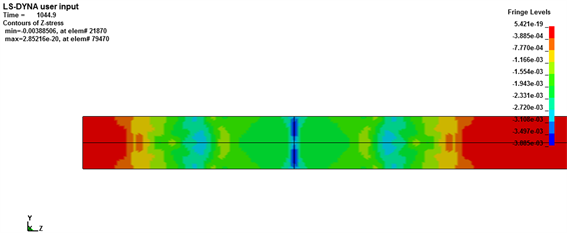 (b)
(b)
Figure 7. Stress diagram for 1/3 unit cell meshing; (a) After contact 8 μs; (b) After contact 45 μs
图7. 1/3单位单元网格划分时应力图;(a) 接触后8 μs;(b) 接触后45 μs
从以上结果中,我们可以知道,在数值模拟过程中,初始阶段,网格的大小是对应力波传播的影响较小,应力波在子弹和入射杆上按一维应力波传导,可忽略应力波的弥散效应,从而得到一维应力波假定和均匀性假定;随着应力波在试件中的传播,网格单元的增大,应力波的分散较为明显。因此,我们认为网格划分的大小,对应力波的传播有显著的影响。在应力波传播过程中,网格划分越小,单位数越多,在同一个速度冲击下,越能够保证应力的集中,越能够满足SHPB实验的一维应力波假定,从而减少数值模拟对SHPB实验结果的影响,得出更为正确的实验结果。
4. 结论
本文利用LS-DYNA建立SHPB模型,对SHPB实验过程进行了数值模拟。通过模拟不同入射速度与不同网格划分的实验过程,并与试件的力学性能进行对比,得到以下结论:
1) 数值模拟可以体现实验过程中试件的力学行为,无论在弹性变形阶段还是在塑性变形阶段均一致。
2) 网格划分的大小对应力波传导有明显的影响,网格划分越小,更加能够减少应力波的弥散效应,提高结果的准确性,这种区别随着接触时间的增加有加大趋势。
3) 建议使用1/3单元网格划分构件,经实验进一步的细化网格,准确度提高不明显,但运算时间会加长。