中心条件充分性的一些证明方法

Some Methods to Prove Sufficient Condition for a Critical Point to Be a Center

摘要: 在微分方程定性理论的学习中，中心充分条件的证明一直是热点以及难点，本文对中心充分条件的一些方法进行归纳总结，利用待定系数法求解积分因子及逆积分因子，解决了两类方程的可积性问题，利用变换的方法解决了一类方程的可积性问题。

Abstract: The sufficient condition for a critical point to be a center in planar qualitative theory has been a hot and difficult problem. Methods of proving the sufficient conditions are summarized, and the sufficiency of two systems was solved by using the method of undetermined coefficient to solve their integral factor and inverse integral factor. Finally, we prove the necessarily by using the transform method.

1. 引言

在微分方程定性理论的学习中，中心焦点判定问题一直是一个热点与难点问题。要证明一个奇点为中心，首先我们要计算其焦点量，当所有的焦点量为零时，我们便得到了系统的奇点为中心的必要条件。但是，众所周知，在证明常微分方程的奇点为中心的充分条件时，难度是非常大的。到目前为止，最常用的办法有三种：1) 证明系统是Hamilton系统；2) 找出系统的积分因子或者逆积分因子；3) 找出系统的首次积分。但是，这三种方法都不能有效解决这类问题时，是否还有其他的办法呢？结合本人的研究经验，本文就这一问题进行一些探讨与总结。

2. 中心条件充分性的几类证明方法

2.1. Hamilton系统

有一些系统很容易直接验证其为Hamilton系统，例如如下系统

$\begin{array}{l}\frac{\text{d}x}{\text{d}t}=-y+\frac{\sqrt{3}{A}_4}{108}{x}^3-\frac{\sqrt{3}{A}_4}{108}x{y}^2=P\left(x,y\right),\hfill \\ \frac{\text{d}y}{\text{d}t}=x+\frac{7\sqrt{3}{A}_4}{108}{x}^{2}y-\frac{\sqrt{3}{A}_4}{36}{y}^3=Q\left(x,y\right).\hfill \end{array}$ (1)

通过直接计算

$\frac{\partial P}{\partial y}+\frac{\partial Q}{\partial x}=0$

即可验证其为Hamilton系统。又因为系统的原点为中心–焦点型奇点，所以系统的原点是中心。但是当系统不是Hamilton系统时就需要我们进行更深入的研究来证明其充分性。

2.2. 积分因子

积分因子在常微分方程教学中属于非常重要的内容，所谓的积分因子就是设法找到一个函数，乘上微分方程后，使得原来的微分方程变成一个全微分方程。关于积分因子的求解也有很多方法，例如观察法、公式法、分项组合法 [1] 等等，有时这些方法都不能起作用，我们就要尝试更为一般的待定系数法。

定义1 [2] ：对于平面多项式系统

$\{\begin{array}{l}\stackrel{\dot{}}{x}=P\left(x,y\right),\\ \stackrel{\dot{}}{y}=Q\left(x,y\right).\end{array}$

如果存在实函数 $V\left(x,y\right)$ 使得

$P\left(x,y\right)\frac{\partial V}{\partial x}+Q\left(x,y\right)\frac{\partial V}{\partial y}=-\left(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}\right)V\left(x,y\right)$

则称 $V\left(x,y\right)$ 是系统的积分因子。

例如系统

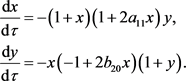(2)

此时容易验证 $\frac{\partial P}{\partial y}+\frac{\partial Q}{\partial x}\ne 0$ ，系统(2)不是Hamilton系统。假设系统(2)有一个三次多项式形式的积分因子

$V\left(x,y\right)=a_0+a_{1}x+a_{2}y+a_3{x}^2+a_{4}xy+a_5{y}^2\text{+}{a}_6{x}^3+a_7{x}^{2}y+a_{8}x{y}^2+a_3{y}^3$

将其代入积分因子满足的公式，借助于计算机代数系统MAPLE，比较两边的系数，容易计算系统(2)有积分因子

$f\left(x,y\right)=\left(1+x\right)\left(1+2a_{11}x\right)\left(1+y\right).$

2.3. 逆积分因子

逆积分因子在大学的常微分课程教学中并没有涉及，但是概念本身非常容易理解。所谓的逆积分因子就是

定义2 [2] ：对于平面多项式系统

$\{\begin{array}{l}\stackrel{\dot{}}{x}=P\left(x,y\right),\\ \stackrel{\dot{}}{y}=Q\left(x,y\right).\end{array}$

如果存在实函数 $V\left(x,y\right)$ 使得

$P\left(x,y\right)\frac{\partial V}{\partial x}+Q\left(x,y\right)\frac{\partial V}{\partial y}=\left(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}\right)V\left(x,y\right)$

则称 $V\left(x,y\right)$ 是系统的逆积分因子。

如果 $V\left(x,y\right)$ 是系统的逆积分因子，则 $1/V\left(x,y\right)$ 为系统的积分因子。有时候积分因子也不容易求出，除了传统的求积分因子的方法可以用来求解逆积分因子，我们仍然可以利用待定系数法求解逆积分因子，利用逆积分因子来证明可积性问题。如下系统

$\begin{array}{l}\stackrel{\dot{}}{x}=y+x\left(\begin{array}{l}{a}_{11}xy-\frac{3}{4}{a}_{40}{y}^2+a_{40}{x}^4+a_{31}{x}^{3}y-\frac{1}{2}{a}_{11}{a}_{40}{x}^2{y}^2\\ +\frac{1}{108}\left(4a_{11}^3-18a_{11}{a}_{31}+27a_{40}^2\right)x{y}^3+\frac{1}{72}{a}_{40}\left(-2a_{11}^2+9a_{31}\right)y^4\end{array}\right),\\ \stackrel{\dot{}}{y}=-2x^3+y\left(\begin{array}{l}{a}_{11}xy-\frac{3}{4}{a}_{40}{y}^2+a_{40}{x}^4+a_{31}{x}^{3}y-\frac{1}{2}{a}_{11}{a}_{40}{x}^2{y}^2\\ +\frac{1}{108}\left(4a_{11}^3-18a_{11}{a}_{31}+27a_{40}^2\right)x{y}^3+\frac{1}{72}{a}_{40}\left(-2a_{11}^2+9a_{31}\right)y^4\end{array}\right).\end{array}$ (3)

利用待定系数法，假设系统(3)有一个四次的逆积分因子

将其代入逆积分因子满足的公式，借助于计算机代数系统MAPLE，比较两边系数，容易求得系统(3)有逆积分因子

$F\left(x,y\right)=x^4+y^2+\frac{1}{3}{a}_{11}{x}^2{y}^2-\frac{1}{2}{a}_{40}x{y}^3+\frac{1}{36}\left(2a_{11}^2-9a_{31}\right)y^4$

2.4. 首次积分

有时系统的积分因子以及逆积分因子都不容易求解，但是有时我们可以直接求出系统的首次积分，例如系统

$\begin{array}{l}\frac{\text{d}u}{\text{d}T}=u\left(1+b_{12}{u}^2+b_{21}uv+b_{22}{u}^{2}v\right),\hfill \\ \frac{\text{d}v}{\text{d}T}=-v\left(1+b_{21}uv+a_{12}{v}^2\text{+}{a}_{\text{2}2}u{v}^2\right).\hfill \end{array}$ (4)

有首次积分

$F\left(u,v\right)=\frac{2u^2{v}^2}{1+b_{12}{u}^2+2b_{21}uv+2b_{22}{u}^{2}v+a_{12}{v}^2+2a_{22}u{v}^2}.$

2.5. 对称变换

最后，当系统既不是Hamilton系统，也不能找出其积分因子或者逆积分因子以及首次积分时，我们可以尝试一些变换将系统转化为对称系统。当然，寻找变换本身没有固定的方法，主要依靠平时的经验总结。例如系统

$\begin{array}{l}\frac{\text{d}x}{\text{d}t}=y-\frac{1}{3}{x}^3+a_{03}{y}^3+30x^{2}y-\frac{547}{54}x{y}^2,\hfill \\ \frac{\text{d}y}{\text{d}t}=-2x^3+x^{2}y-\frac{1}{6}{y}^3-\frac{10}{9}x{y}^2.\hfill \end{array}$

可以通过变换

$x=\frac{1}{6}\left(-u+v\right),y=v.$

转化为对称系统

Figure 1. The programme for proof of integrability

图1. 证明可积性步骤

3. 总结

因此，今后证明一般系统的可积性的必要条件时，我们可以遵循如图1所示的方法。