1. 引言
在高温环境下工作时,人们需要穿着专用服装以避免灼伤。专用服装通常由三层织物材料构成,记为I、II、III层,其中I层与外界环境接触,III层与皮肤之间还存在空隙,将此空隙记为IV层。为设计专用服装,将体内温度控制在37℃的假人放置在实验室的高温环境中,测量假人皮肤外侧的温度。为了降低研发成本、缩短研发周期,我们建立利用数学模型来确定假人皮肤外侧的温度变化情况,具体解决以下问题:
1) 专用服装材料的密度、比热、热传导率等物理参数已知条件下(见全国大学生数学建模竞赛附件1),对环境温度为75℃、II层厚度为6 mm、IV层厚度为5 mm、工作时间为90分钟的情形开展实验,测量得到假人皮肤外侧的温度(见全国大学生数学建模竞赛附件2)。建立数学模型,计算专用服装的温度分布。
2) 当环境温度为65℃、IV层的厚度为5.5 mm时,确定II层的最优厚度,确保工作60分钟时,假人皮肤外侧温度不超过47℃,且超过44℃的时间不超过5分钟。
3) 当环境温度为80时,确定II层和IV层的最优厚度,确保工作30分钟时,假人皮肤外侧温度不超过47℃,且超过44℃的时间不超过5分钟。
2. 模型假设
1) 假设专用服装材料I、II、III各层材料的密度、比热、热传导率等物理参数均匀同质,并且不随时间和温度的改变而改变。
2) 本文不考虑专用服装材料I、II、III各层材料的热胀冷缩效应,即I、II、III各层材料的厚度不随温度的改变而改变。
3) 辐射只有在高温下才能成为主要的传热方式(本文的最高温度80℃,远远小于500℃),对流需要较大的空间(第IV层空隙封闭狭窄),因此热的传导是各层材料间的热量的传递主要方式,本文不考虑热的辐射传递和对流传递。
4) 假设服装I层外侧的环境温度均匀一致,并且恒定不变。
5) 假设身着高温作业专用服装的假人体内温度为37℃,并且恒定不变,但是体内温度不等同皮肤温度,我们认为温度变化的皮肤到温度恒定的体内存在一个热传导的过程,其间存在一定的介质,本文后面将对这里提到的介质作进一步的假设。
6) 假设专用服装的各层材料的初始温度相同。
7) 假设附件提供的物理参数和测量皮肤外侧的温度是准确的,并且认为皮肤外侧的温度即为第IV层内侧的温度。
3. 符号说明
4. 模型的建立
4.1. 温度分布模型的建立
由假设4,热量在各层间的传递近似地看作一维热传导方程推导 [1] [2] [3] [4] 。因此,如下模型作为
基本模型,研究各层温度的分布及变化
。
由假设1,专用服装材料I、II、III、IV各层材料的密度、比热、热传导率等物理参数均匀同质,并且不随时间和温度的改变而改变,但是I、II、III、IV各层材料的密度、比热、热传导率等物理参数不相同,所以k分段计算。
由假设6,专用服装的各层材料的初始温度相同,设
由假设7,将其温度随时间的变化记作函数
,即
综上所述,问题一要求在专用服装材料厚度,参数值的厚度、密度、比热、热传导率等物理参数给定的条件下温度分布的计算,可转化为以下初值和边界条件下的微分方程的求解。
模型1:皮肤温度已知的专用服装材料温度分布模型
方程:
其中
。
初值条件:
边界条件:
4.2. 第II层厚度的优化模型的建立
问题要求环境温度为65℃、IV层的厚度为5.5 mm时,确定II层的最优厚度,确保工作60分钟时,假人皮肤外侧温度不超过47℃,且超过44℃的时间不超过5分钟。
问题2与问题1比较,不同的地方在于:问题1给出了专用服装靠近皮肤端的边界随时间温度变化情况(表皮温度的测量值),而问题2没有给出专用服装靠近皮肤端的边界随时间温度变化情况。
问题的难点:确定专用服装靠近皮肤端的边界温度变化情况。
根据“假人体内温度控制在37℃”的已知条件,针对专用服装靠近皮肤端的边界温度变化情况未知,为此我们提出以下假设
假设5、假设身着高温作业专用服装的假人体内温度为37℃,并且恒定不变,但是体内温度不等同皮肤温度,我们认为温度变化的皮肤到温度恒定的体内存在一个热传导的过程,其间存在一定的介质。
问题的方案:皮肤到温度恒定的体内存在一个热传导的过程,将其简化看作长度一定的均匀介质,称为第五层(图1)。记第五层热扩散率为
,长度为
。
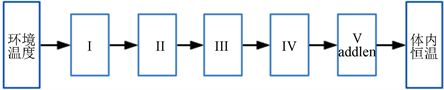
Figure 1. Schematic diagram of the five-layer heat conduction model
图1. 五层热传导模型示意图
问题二要求“在环境温度为65℃、IV层的厚度为5.5 mm时,确定II层的最优厚度,确保工作60分钟时,假人皮肤外侧温度不超过47℃,且超过44℃的时间不超过5分钟”的问题,可转化为以下优化模型。
模型2:第II层厚度的优化模型
使得满足
1) 方程:
其中 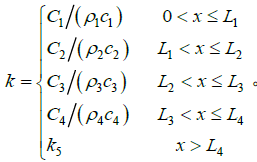 。
。
2) 初值条件:
3) 边界条件:
,
其中
, 分别为第四层内侧(皮肤表层)在时刻
秒(55分钟)和
秒(60分钟)的温度。
分别为第四层内侧(皮肤表层)在时刻
秒(55分钟)和
秒(60分钟)的温度。
4.3. II层和IV层的最优厚度模型的建立
问题要求环境温度为80℃时,确定II层和IV层的最优厚度,确保工作30分钟时,假人皮肤外侧温度不超过47℃,且超过44℃的时间不超过5分钟。
问题分析:无论增加II层还是IV层的厚度都会降低皮肤温度的上升速率和最终温度,因此确定II层和IV层的最优厚度的问题,我们可以理解为使得总厚度最小的II层和IV层的厚度。
模型3:II层和IV层厚度的优化模型
其中
,
分别为第四层内侧(皮肤表层)在时刻
秒(55分钟)和
秒(60分钟)的温度。
,
由模型2模拟计算(其边界条件:
,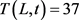 ),热扩散率为
,长度为
)。
),热扩散率为
,长度为
)。
5. 模型求解
5.1. 模型1的求解
模型1是典型的抛物椭圆偏微分方程,我们基于MATLAB的抛物椭圆偏微分方程求解器pdepe求解 [5] [6] [7] [8] [9] 。观察附件2中的数据,0~15秒测得皮肤外侧的温度都是不变的(或很微小),第16秒温度开始升高,若高温作业专用服装的温度高于37℃,则测量的温度在短时间内高于37度,若高温作业专用服装的温度高于37℃,热量向服装传递,会使得测量的温度在短时间内下降,低于37℃。因此这里可认为高温作业专用服装的温度为37℃。计算结果图2~4,揭示温度分布的渐变过程和最终分布特点:1) 高温作业专用服装温度分布曲线随时间逐渐变化,最终为四段直线构成的折线,分段点为不同材料的
分界点(图2,图3),直线的斜率与热扩散率
成正比。2) 高温作业专用服装温度变化曲线随位置
逐渐变化,靠近外界的位置温度变化快,远离外界的位置温度变化稍慢,最终为温度恒定不变(图2,图4)。

Figure 2. Temperature distribution of special clothing for high-temperature operation
图2. 高温作业专用服装的温度分布

Figure 3. Temperature distribution of special clothing for high-temperature operation at a specific time
图3. 特定时间高温作业专用服装的温度分布
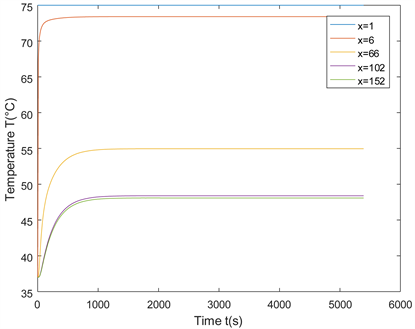
Figure 4. Temperature variation of special clothing for high-temperature operation at a specific location
图4. 特定位置高温作业专用服装的温度变化
5.2. 模型2的求解
如果模型2关于第五层的假设是合理的,那么使用模型2求解问题1的结果(第四层内侧的温度)与题目附件提供的皮肤的测量温度应该一致或接近。为此,我们可以通过拟合确定第五层热扩散率为
,长度为
。
第五层热扩散率为
,长度为
的确定模型
其中
为第四层内侧(皮肤表层)的温度由模型2计算,
为附件提供的皮肤表层测量温度。
我们使用MATLAB的用遗传算法寻找函数的最优解的求解器ga [10] [11] [12] 求解第五层热扩散率为
,长度为
的确定模型,我们得到最优的扩散系数为
,V层厚度
,误差平方和
,
,拟合结果效果如图5。RMSEn的值和拟合结果效果图都表明拟合效果很好。因此,皮肤到温度恒定的体内的热传导过程,简化长度一定的均匀介质的热传导过程是合理的,并且该均匀介质(第五层)的热扩散率为
,长度为
,皮肤温度与测量温度的对照见图5。

Figure 5. The comparison between the calculated skin temperature and the measured temperature at
图5.
,
时计算的皮肤温度与测量温度的对照
确定第五层的热扩散率为
,长度为
后,模型2的求解,可采用搜索方法计算(
的取范围:0.6~25 mm,考虑工业水平的限制步长取0.1即可,总的搜索次数最多250次),这里我们可以先取较大的步长,然后细化,以节约时间。

Table 1. The solution of problem two
表1. 问题二的求解结果
说明:其中l2为II层的厚度(mm),t44为皮肤温度达到为44℃时对应的时间(s);t47为皮肤温度达到为47℃时对应的时间(s),T3300为工作3300秒的皮肤温度,T3600工作3600秒的皮肤温度,Tlast为服装温度分布稳定后皮肤温度。
表1揭示:1) 在问题二的条件下,服装的II层的厚度越厚,长时间工作越安全。2) 在问题二的条件下,服装的II层的最低厚度l2 = 8.11 mm,此时工作时,工作一小时,皮肤的最高温度低于44℃。3)在问题二的条件下,服装的II层的厚度为l2 = 8.11 mm时,皮肤的最高温度为43.95℃,非常温度接近44℃。并且若要持续工作60分钟,须在皮肤温度为43.6℃的条件下长时间工作,所以为安全着想,设计服装的II层的厚度应大于8.1 mm,最好在l2 = 8.6 mm以上。
5.3. 模型3的求解
皮肤温度基于MATLAB的抛物椭圆偏微分方程求解器PDEPE模拟;优化问题采用搜索方法计算(
的取范围:0.6~25 mm,
的取范围:0.6~6.4 mm,考虑工业水平的限制步长取0.1即可,总的搜索次数不超过1500次)。

Figure 6. Simulation of temperature change inside layer IV
图6. IV层内侧温度变化的模拟
图6表明加厚II层比加厚IV层隔热效果明显很多,所以我们采取厚度优化策略为:优先确定II层的厚度。
计算结果表明II层的厚度至关重要,最低厚度15.3 mm,才可能有满足安全工作需求的设计;II层为15.5 mm,IV层为0.6 mm,总厚度最小;II层为15.5 mm时,IV层厚度随意设计都满足安全工作需求。
6. 模型的检验
6.1. 传导方程的检验
本文基于假设,利用热传导理论和热平衡理论建立了高温专用服装各层的热传导模型,模型模拟温度分布的特点:1) 高温作业专用服装温度变化曲线随位置逐渐变化,靠近外界的位置温度变化快,远离外界的位置温度变化稍慢,最终为温度恒定不变;2) 高温作业专用服装温度分布曲线随时间逐渐变化,
最终为四段直线构成的折线,分段点为不同材料的分界点,直线的斜率与热扩散率
成正比。以上结论符合我们对热传递的常识,因此以
为传导方程是合理的。
6.2. IV层内侧热传递模型的检验
本文将皮肤到温度恒定的体内的热传导的过程,简化看作热在长度一定的均匀介质中的传导的过程,称为第五层。记第五层热扩散率为
,长度为
。我们使用最小二乘拟合得到扩散系数为
,V层厚度
。这时,误差平方和
,模拟值与观测值的标准均方根误差
,拟合结果效果如图5。RMSEn的值和拟合结果效果图都表明拟合效果很好。因此,皮肤到温度恒定的体内的热传导过程,简化长度一定的均匀介质的热传导过程是合理的,并且该均匀介质(第五层)的热扩散率为
,长度为
。
7. 模型的改进和应用
高温专用服装的设计过程中衣服的厚度(也包括成本)很重要,但是最重要的是安全性,因此在保证安全的条件下优化厚度才是有意义有价值的,为此本文模型可从以下几个方面改进。
1) 在本文模型的基础上对安全性进行实际检验,确定符合安全性要求“皮肤到温度恒定的体内的热传导的过程,简化看作热在长度一定的均匀介质中的传导过程”的参数确定方案、而不是以拟合程度最佳为依据;
2) 优化模拟程序,提高程序的运行速度和智能化程度。
模型在经过安全性实际检验和优化后,可应用于高温专用服装的设计和其他耐高温产品的研发。
基金项目
湖南农业大学教改课题(2017024,农业大学基础学科人才培养支持优势学科发展的对策研究);湖南农业大学大学生创新性实验计划项目(基于随机模型简化水稻三维形态结构数字化和可视化构造的研究)。
参考文献
NOTES
*通讯作者。