1. 引言
证据理论具有较强的理论基础,既能处理随机性所导致的不确定性,又能处理模糊性所导致的不确定性 [1] [2] ,利用Dempster组合规则可以对不同传感器提供的目标识别证据进行空间域判决融合 [3] ,还可以在时间域对传感器提供的目标识别证据进行时间域融合 [4] ,证据理论可以依靠证据的积累,不断缩小假设集 [5] 。K近邻(K-Nearest Neighbor, KNN)算法是一种比较成熟的分类算法,也是最简单的机器学习算法之一 [6] 。近年来利用K近邻算法进行的识别与分类被广泛应用于各行各业,例如文献 [7] 将其与支持向量机相融合应用于天气识别领域,文献 [8] 将其应用于醉酒驾驶识别领域,等等。经典的K近邻算法仅适用于边界可分和类分布为椭圆和高斯分布的情况 [9] ,一旦突破这个前提,K近邻分类器的分类效果就会不理想。针对这个问题,很多专家学者对经典K近邻算法进行了改进。文献 [10] 中,Zouhal利用统计学习的方法对经典K近邻算法进行了优化,用一个基本概率赋值(Basic Probability Assignment, BPA)函数表示一个测试样本属于某一目标类的可能性,并且将该函数随距离的变化用负指数函数表示。
本文所提出的基于证据K近邻的目标识别新方法就是在Zouhal方法基础上的改进,当利用求得的参考最近邻距离和证据理论得出初始的识别分类结果后,引入混淆矩阵
,利用初始分类结果与训练样本真值之间的偏差对结果进行修正,使得分类结果更加准确,识别率提高,然后,通过多数据集验证了
矩阵的泛化能力,通过与经典算法的分类精度对比验证了新方法的可行性和有效性。
2. K近邻算法
K近邻(K-Nearest Neighbor, KNN)算法是在1968年由Cover和Hart提出来的 [11] ,它是一种理论比较成熟的分类算法,也是最简单的机器学习算法之一。
2.1. 算法思路及特点
该算法的思路是:如果一个样本在特征空间中的K个最相似(也就是特征空间中的K个最近邻)样本中的大多数属于某一识别类,则认为该样本属于此识别类。
在K-NN算法中,所选择的邻居都是已经正确分类的对象,该算法在分类决策上只依据最近邻的一个或者几个样本的类别来决定待测样本的类别。
该算法的特点是:①基于实例之间距离和投票表决的分类②适合多分类③大多数情况下比贝叶斯和中心向量法好④当给定训练集、距离度量、K值及分类决策函数时,结果唯一确定。
2.2. 算法描述
假设训练数据集
,其中,
为实例的特征向量,
为实例的分类。根据给定的距离度量
(使用的距离度量不同,K近邻的结果也会不同,本文取Euclid距离)即
(1)
其中,
,
,
。
在训练集T中找出与实例向量
最近的K个点,涵盖着K个点的
的邻域记作
,在
中根据分类决策规则(如投票表决)决定
所属的类别y,即
(2)
其中,
,
,I为指示函数,即当
时,I为1,否则为0。
因此,K-NN算法中,当训练集、距离度量、K值及分类规则确定后,对于任意一个输入实例
,它所属的目标类y是唯一确定的。
3. 证据K近邻规则
K近邻算法的一个显而易见的改进是对K个近邻的贡献进行加权 [12] ,根据它们相对待识别样本
的距离,将较大的权值赋给较近的近邻,因此,引入证据理论中,基本概率赋值函数的规律应该随距离的增大而减小,这里取负指数函数来表达 [10] ,即
(3)
其中,
,
根据经验设定取0.95,
为第k个近邻到实例向量
的距离。则输出的识别分类结果为
(4)
按照上述距离加权的K近邻算法是一种非常有效的归纳推理算法,它对训练中的噪声有很好的鲁棒性 [13] ,并且当给定足够大的训练集合时,它也是非常有效的,本论文将在后续小节进行验证。
基于距离加权的K近邻算法引入到证据理论中,可以将权重系数作为证据理论中相关信息的基本概率赋值,则有
 ,
(5)
,
(5)
证据K近邻规则的思路可以概括为:利用每个近邻的基本概率赋值作为证据理论的BPA赋值,并完成最终分类。即假设现有一个待识别样本
,它的K个近邻为
,根据式(3)和(5)可以得到每个近邻的基本概率赋值
,再利用Dempster组合规则进行合成,算出
属于某个目标类的置信度完成最终分类。
4. 新算法
4.1. 新算法的思想
距离
所包含的信息不仅与其所对应的训练样本中属于目标类y的那部分训练样本有关,还与训练样本中不属于目标类y的那部分训练样本有关。对于任意一个目标类y的样本而言,假设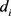 是它与目标类y内的最近邻之间的距离,若
,则认为该样本不属于目标类y;若
是它与目标类y内的最近邻之间的距离,若
,则认为该样本不属于目标类y;若 ,则认为该样本属于目标类y。证据K近邻的目标就是在误分配率最小化的前提下完成样本的分类,因此,在一定程度上,距离信息
可以看作是一个阈值,以距离信息
为门限在误分配率最小化的前提下进行样本分类。这里就存在一个误分配率的问题,它所代表的物理意义是目标类y与其他目标类的混淆程度,即使是在其最小化的前提下进行的分类,它也会对最终的结果造成不良的影响,本文就是从该误分配率着手,引入混淆矩阵
,利用初始分类结果与训练样本真值之间的偏差对结果进行修正,使分类结果更加精确。
,则认为该样本属于目标类y。证据K近邻的目标就是在误分配率最小化的前提下完成样本的分类,因此,在一定程度上,距离信息
可以看作是一个阈值,以距离信息
为门限在误分配率最小化的前提下进行样本分类。这里就存在一个误分配率的问题,它所代表的物理意义是目标类y与其他目标类的混淆程度,即使是在其最小化的前提下进行的分类,它也会对最终的结果造成不良的影响,本文就是从该误分配率着手,引入混淆矩阵
,利用初始分类结果与训练样本真值之间的偏差对结果进行修正,使分类结果更加精确。
4.2. 混淆矩阵P的定义与求解
混淆矩阵也称作误差矩阵 [14] ,在人工智能中它被看作是一种可视化工具,可用于监督学习 [15] ,在图像精度评价中,主要用于比较分类结果和实际测得值 [16] ,可以把分类结果的精度显示在一个混淆矩阵里面 [17] ,利用这一思想,本文引入一个混淆矩阵
如下:
(6)
其中,
表示实际属于第j个目标类却被误分配给第i个目标类的概率。
首先,利用BP神经网络对训练样本进行训练,找到目标样本的K个近邻,用
表示,通过预先设定的分类器C对这K个近邻进行分类输出,其中任意一个样本
经过分类器输出后得到的结果为
,
表示通过设定的分类器得到目标样本的近邻
属于类别
的概率。假设
的真实分类为
,则用
表示期望的分类器输出值。
假设共有C个目标类记作
,某待测样本
有K个近邻,通过证据K近邻规则(见第2节)算得待测样本
归为目标类
,并且通过式(3)和(5)得出权重系数
,即
(7)
然后,在K个近邻中找出被分给目标
类的样本,假设有N个,计算这N个近邻被修正后的值(即
)与训练样本真值T之间的偏差和(这里取Euclid距离),即
(8)
将式(8)最小化算得
,即为所求混淆矩阵。
4.3. 新算法的步骤
基于上述算法思想及相关基础解析,新算法的步骤可以概括为:
①选取数据集样本进行训练,得出初始目标类和聚类中心;
②利用证据K近邻规则计算待测样本的初始分类结果;
③由式(8)最小化算得混淆矩阵
;
④利用混淆矩阵
对结果进行修正,得出最终分类结果
,其中
。
5. 实验仿真与分析
为了验证第3节所说的“当给定足够大的训练集合时本文算法依然非常有效”的说法,这里选取Satimage数据集来进行仿真验证和深入分析。为了验证混淆矩阵
的泛化能力还选取了其他6组数据集进行验证,并将本文方法与经典Bayes及经典ENN方法进行了对比。
5.1. 仿真步骤
Satimage数据集共有6435个样本,这里将样本一分为二,一半作为训练样本,一半作为测试样本。
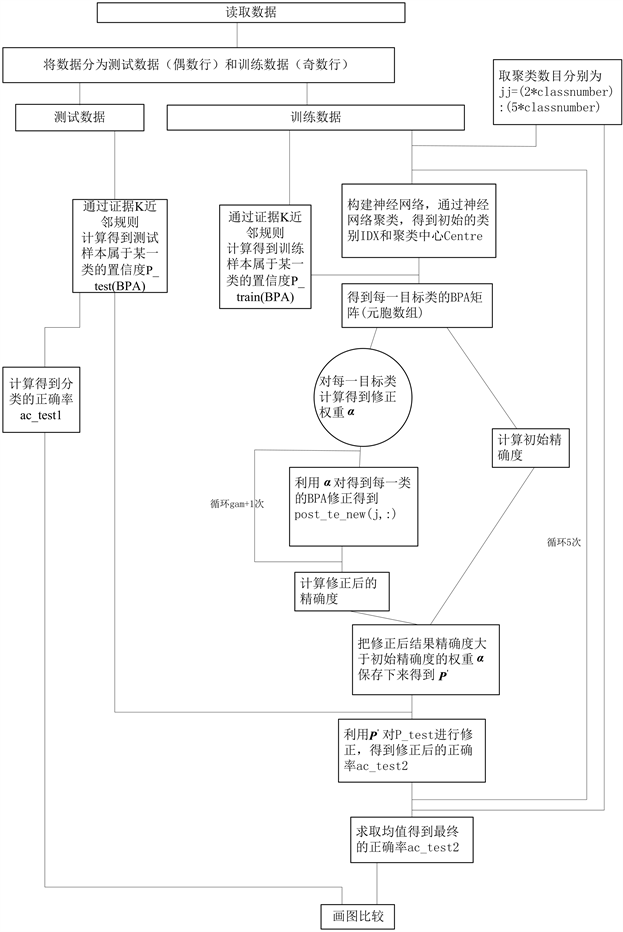
Figure 1. New algorithm MATLAB simulation flow chart
图1. 新算法MATLAB仿真流程图
首先,构建神经网络对训练样本进行训练并得到初始的分类类别和聚类中心;其次,通过证据K近邻规则算出训练样本中每一个样本属于某一目标类别的BPA,得到每一目标类别的BPA矩阵;第三,计算每一个目标类的权重系数
,得出混淆矩阵
(见4.2节);第四,利用混淆矩阵
对初始结果进行修正,计算修正后的识别精确度;第五,重复迭代,将修正后的识别精确度大于初始识别精确度的权重系数
保存下来,构成最终的修正矩阵
;第六,一方面,测试样本根据证据K近邻规则算出初始分类结果,另一方面,用训练样本算出的最终的修正矩阵
对测试样本的初始分类结果进行修正,得到修正后的分类结果;最后,将测试样本初始分类识别精确度与修正后的识别精确度进行比较并作图。
Matlab仿真流程如图1所示。
5.2. 实验结果分析
通过本文所提的新算法,利用Satimage数据集进行实验仿真后,可以得到初始分类识别精确度与修正后分类识别精确度如表1所示,对比图如图2所示。
由表1及图2可以形象直观地看出,新方法在引入混淆矩阵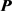 对初始分类结果进行修正后所得到的
对初始分类结果进行修正后所得到的

Table 1. Comparison of initial classification recognition accuracy and corrected classification identification accuracy
表1. 初始分类识别精确度与修正后分类识别精确度对比表
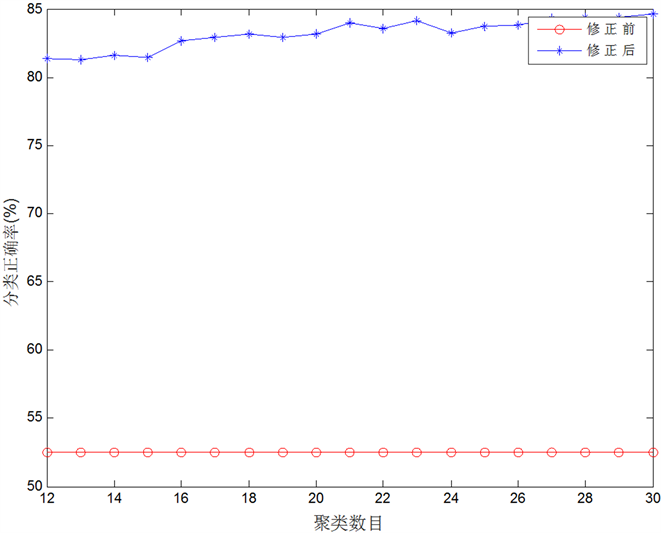
Figure 2. Correction of classification and recognition accuracy before and after correction
图2. 修正前后分类识别精确度对比图
目标识别分类结果的精确度要远远高于仅利用证据K近邻规则所得的目标识别分类结果的精确度。修正前的分类精度因为没有对样本进行训练和修正的过程,所以其精度不会随着聚类数目的增多而发生变化。而本文所提的新方法利用混淆矩阵
对初始分类结果进行不断修正且有对样本进行训练的过程,所以该新方法在聚类数目增多的情况下,分类精度会随之增高。
为了验证混淆矩阵
的泛化能力,随机选取了其他6组数据集(Sonar、Vehicle、Page、Vowel、Wine-red和Segment)进行验证,并将本文方法与经典Bayes及经典ENN方法进行了对比。见表2。
由表2可知,
阵具有很好的泛化能力,对训练样本依赖不大,不光是Satimage数据集,其他数据

Table 2. Comparison of classification accuracy of different classification ideas
表2. 不同分类思想分类精度对比
集也同样适用。通过实验结果对比可以看出基于证据K近邻的目标识别新方法较Bayes及经典ENN算法分类精度有较大提高,具有现实意义且行之有效。
6. 结论
本文提出了一种基于证据K近邻的目标识别新方法,在Zouhal改进KNN算法的基础上增加了训练修正步骤。首先,求得每一个目标类别的参考最近邻距离,使训练样本中该目标类别的样本在经验风险最小化的前提下与其他样本完成分离;然后,利用求得的参考最近邻距离和证据理论结合得出初始的识别分类结果;第三,设置混淆矩阵
,通过神经网络寻优迭代,获得
矩阵参数,用于Zouhal分类结果修正;最后,通过多数据集验证了
矩阵具有很好的泛化能力,对训练样本依赖不大,且通过实验结果对比可以看出基于证据K近邻的目标识别新方法较Bayes及经典ENN算法分类精度有较大提高,具有现实意义且行之有效。
基金项目
国防科技卓越青年人才基金(2017-JCJQ-ZQ-003),泰山学者工程专项经费(ts201712072),国家自然科学基金(61501488)资助课题。