1. 引言
1.1. 研究背景
设
为正整数,满足
。一个设计
或t-设计
定义为符合以下条件的一对符号
,满足:
1)
是有v个点的有限集,
的元素为点;
2)
是
的一组k-子集,
的元素称为区组或区;
3)
的任意给定的t-子集都恰好包含在
的
个区组之中。
这里r是过一个点的区的个数,b是区组的总数。我们总假设B的成员都不相同,即B中的区组不允许重复出现,称
为设计D的参数。当
时,称t-设计
是非平凡的。
设计
的一个旗是指点–区对
,这里
,
且
。
,若G在
上的作用是本原的,称G是点本原的。若G在
的旗的集合上是传递的,称G或者
是旗传递的。
1988年,P. H. Zieschang [1] 已经证明若G是一个旗传递
设计的自同构群且
,T是G的一个极小正规子群那么T是仿射型或者几乎单型。Regueiro [2] 证明了当
时,G是仿射型或者几乎单型。当
时 [3] [4] ,可以得到相同的结果。2013年周胜林和田德路 [5] 证明了若G旗传递、点本原作用在
上且
,则G是仿射型或者几乎单型。最近梁洪雪和周胜林 [6] 分析了
是非对称的情况,并证明了一个旗传递、点本原、非对称
设计的自同构群是仿射型或者几乎单型。
本文研究了旗传递、点本原
设计当
且自同构群G为Suzuki群时的情况,得到如下结果:
设D是一个非平凡的
设计,其中
,若
是D的旗传递、点本原的自同构群。则D是一个
设计,且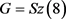 。
。
1.2. 预备知识
引理1: [7] 若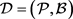 是一个
是一个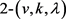 设计。则下面式子成立:
设计。则下面式子成立:
1)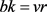 ;
;
2)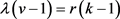 ;
;
3)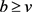 。
。
引理2: [8] 设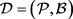 是一个
是一个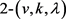 设计,
设计,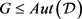 ,对任意的
,对任意的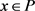 和
和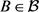 ,则G在
,则G在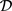 上旗传递等价于下列的条件之一:
上旗传递等价于下列的条件之一:
1) G是点–传递的,并且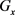 在P(x)上传递;
在P(x)上传递;
2) G是区–传递的,并且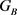 在B上传递。
在B上传递。
引理2: [8] 设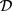 是一个
是一个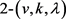 设计且
设计且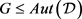 是旗传递的,则
是旗传递的,则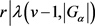 ,其中
,其中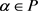 。
。
引理4: [9] 设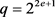 ,e是一个正整数,则
,e是一个正整数,则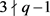 ,
,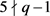 。
。
证明: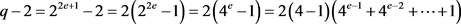 ,得到
,得到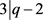 。由
。由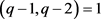 ,得到
,得到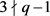 。
。
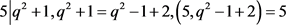 ,得到
,得到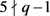 。
。
2. 定理1的证明
设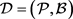 是一个满足
是一个满足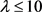 的
的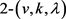 设计,
设计,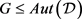 是旗传递、点本原的群,且
是旗传递、点本原的群,且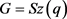 。
。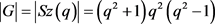 ,其中
,其中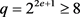 。G的极大子群
。G的极大子群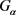 的阶有4种情况,分别是
的阶有4种情况,分别是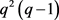 、
、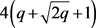 、
、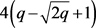 和
和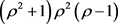 。其中
。其中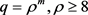 并且
并且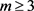 。现在我们来讨论点稳定子群
。现在我们来讨论点稳定子群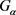 的阶在4种情况下,设计是否存在。
的阶在4种情况下,设计是否存在。
引理5: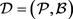 是一个满足
是一个满足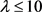 的
的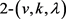 设计,
设计,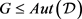 是旗传递、点本原的群,且
是旗传递、点本原的群,且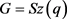 。若
。若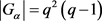 ,则D是一个
,则D是一个 设计,且
设计,且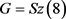 。
。
证明: ,则
,则

由于G是旗传递的,并且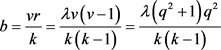 ,可以得到
,可以得到
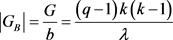
由于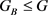 ,则必存在G的一个极大子群L,使得
,则必存在G的一个极大子群L,使得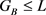 。
。
首先假设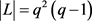 ,则
,则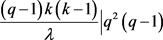 ,因此
,因此 。
。
由于G旗传递,可以得到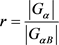 。而
。而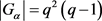 。故
。故 。
。
若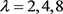 ,则
,则 ,其中i是自然数,由
,其中i是自然数,由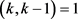 可以得出k = 2与
可以得出k = 2与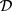 非平凡矛盾。
非平凡矛盾。
若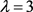 ,则
,则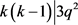 ,得出
,得出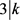 或者
或者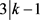 。否则,则
。否则,则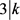 且
且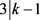 ,此时可以得到
,此时可以得到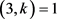 且
且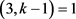 ,即
,即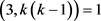 ,故
,故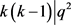 。而
。而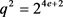 ,因此可以得到
,因此可以得到 ,i是自然数且
,i是自然数且 ,j是自然数。又
,j是自然数。又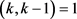 ,可以得到
,可以得到 ,即
,即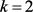 ,与D非平凡矛盾。故而
,与D非平凡矛盾。故而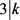 或者
或者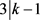 。
。
若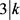 ,则
,则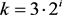 ,其中i是自然数,
,其中i是自然数,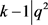 ,由于
,由于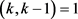 ,得出i = 0,k = 3。
,得出i = 0,k = 3。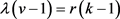 即
即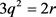 ,得出
,得出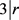 ,又
,又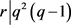 ,得出
,得出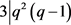 。与引理4矛盾。
。与引理4矛盾。
若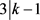 ,则
,则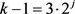 ,其中j是自然数,
,其中j是自然数,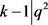 ,由于
,由于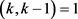 ,得出j = 0,k = 4。已知G在v个点上是2-传递的 [10] ,则
,得出j = 0,k = 4。已知G在v个点上是2-传递的 [10] ,则
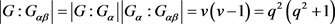
因此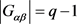 。记Q是包含一些区的集合,且Q里的区均包含
。记Q是包含一些区的集合,且Q里的区均包含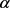 和
和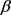 。则
。则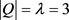 。
。
现在证明存在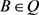 ,使得
,使得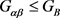 。否则
。否则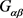 不固定Q中任一个区,则
不固定Q中任一个区,则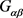 在Q上传递,且
在Q上传递,且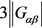 。又
。又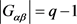 。与引理4矛盾。所以一定存在
。与引理4矛盾。所以一定存在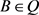 ,使得
,使得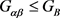 。
。
已知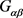 半正则作用于
半正则作用于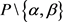 [10] ,则
[10] ,则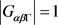 ,任取
,任取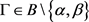 。故
。故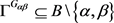 ,得出
,得出 ,则
,则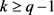 。与k = 4矛盾。
。与k = 4矛盾。
若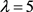 ,则
,则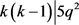 ,得出
,得出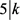 或者
或者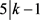 。否则,则
。否则,则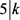 且
且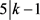 ,此时可以得到
,此时可以得到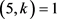 且
且 ,即
,即 ,故
,故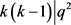 。而
。而 ,因此可以得到
,因此可以得到 ,i是自然数且
,i是自然数且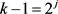 ,j是自然数。又
,j是自然数。又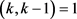 ,可以得到
,可以得到 ,即
,即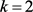 ,与D非平凡矛盾。故而
,与D非平凡矛盾。故而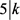 或者
或者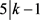 。
。
若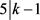 ,则
,则 ,其中j是自然数,
,其中j是自然数,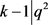 ,由于
,由于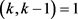 ,得出i = 0,k = 6,与
,得出i = 0,k = 6,与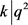 矛盾。
矛盾。
若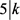 ,则
,则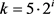 ,其中i是自然数,
,其中i是自然数,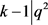 ,由于
,由于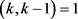 ,得出i = 0,k = 5。
,得出i = 0,k = 5。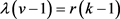 即
即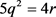 ,得出
,得出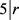 ,又
,又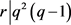 ,得出
,得出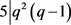 。与引理4矛盾。
。与引理4矛盾。
若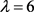 ,则
,则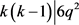 ,得出
,得出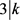 或者
或者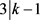 。否则,则
。否则,则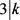 且
且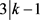 ,此时可以得到
,此时可以得到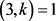 且
且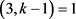 ,即
,即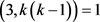 ,故
,故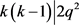 。而
。而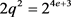 ,因此可以得到
,因此可以得到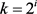 ,i是自然数且
,i是自然数且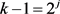 ,j是自然数。又
,j是自然数。又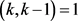 ,可以得到
,可以得到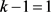 ,即
,即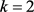 ,与D非平凡矛盾。故而
,与D非平凡矛盾。故而 或者
或者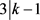 。
。
若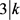 ,则
,则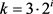 ,其中i是自然数,
,其中i是自然数,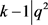 ,由于
,由于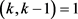 ,得出i = 0,,k = 3。
,得出i = 0,,k = 3。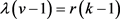 即
即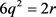 ,得出
,得出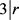 ,又
,又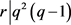 ,得出
,得出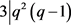 。与引理4矛盾。
。与引理4矛盾。
若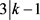 ,则仿照证明
,则仿照证明 的方法可得k = 4,此时
的方法可得k = 4,此时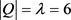 。
。
现在证明存在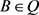 ,使得
,使得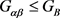 。否则
。否则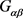 不固定Q中任一个区。此时
不固定Q中任一个区。此时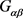 的轨道长度可能为2,3,4,6,都不能整除
的轨道长度可能为2,3,4,6,都不能整除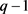 ,得出矛盾。所以一定存在
,得出矛盾。所以一定存在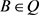 ,使得
,使得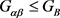 。
。
已知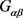 半正则作用于
半正则作用于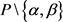 ,则
,则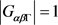 ,任取
,任取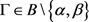 。故
。故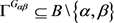 ,得出
,得出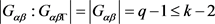 ,则
,则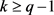 。与k = 4矛盾。
。与k = 4矛盾。
若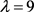 ,则
,则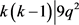 ,得出
,得出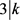 或者
或者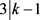 。否则,则
。否则,则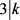 且
且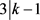 ,此时可以得到
,此时可以得到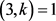 且
且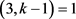 ,即
,即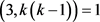 ,故
,故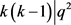 。而
。而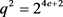 ,因此可以得到
,因此可以得到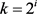 ,i是自然数且
,i是自然数且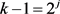 ,j是自然数。又
,j是自然数。又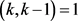 ,可以得到
,可以得到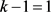 ,即
,即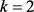 ,与D非平凡矛盾。故而
,与D非平凡矛盾。故而 或者
或者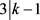 。
。
若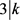 ,则
,则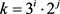 ,其中i = 1,2,j是自然数,
,其中i = 1,2,j是自然数,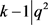 ,由于
,由于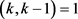 ,得出i = 0,k = 3。
,得出i = 0,k = 3。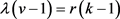 ,若k = 3,则
,若k = 3,则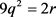 ,得出
,得出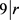 ,又
,又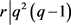 ,得出
,得出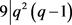 。与引理4矛盾。若k = 9,则
。与引理4矛盾。若k = 9,则 ,得出
,得出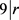 ,又
,又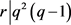 ,得出
,得出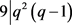 。与引理4矛盾。
。与引理4矛盾。
若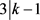 ,则仿照证明
,则仿照证明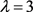 的方法可得k = 4。
的方法可得k = 4。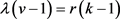 即
即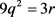 ,得出
,得出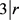 ,又
,又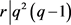 ,得出
,得出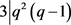 。与引理4矛盾。
。与引理4矛盾。
若 ,则
,则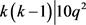 ,得出
,得出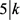 或者
或者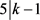 。否则,则
。否则,则 且
且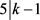 ,此时可以得到
,此时可以得到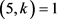 且
且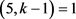 ,即
,即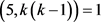 ,故
,故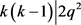 。而
。而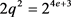 ,因此可以得到
,因此可以得到 ,i是自然数且
,i是自然数且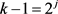 ,j是自然数。又
,j是自然数。又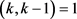 ,可以得到
,可以得到 ,即
,即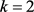 ,与D非平凡矛盾。故而
,与D非平凡矛盾。故而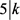 或者
或者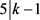 。
。
若 ,则
,则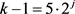 ,其中j是自然数,
,其中j是自然数,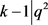 ,由于
,由于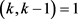 ,得出i = 0,k = 6,与
,得出i = 0,k = 6,与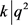 矛盾。
矛盾。
若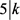 ,则
,则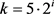 ,其中i是自然数,
,其中i是自然数,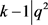 ,由于
,由于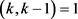 ,得出i = 0,k = 5。
,得出i = 0,k = 5。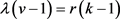 即
即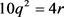 ,得出
,得出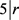 ,又
,又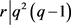 ,得出
,得出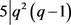 。与引理4矛盾。
。与引理4矛盾。
若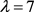 ,则
,则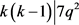 ,得出
,得出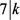 或者
或者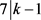 。否则,则
。否则,则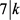 且
且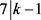 ,此时可以得到
,此时可以得到 且
且 ,即
,即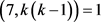 ,故
,故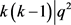 。而
。而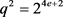 ,因此可以得到
,因此可以得到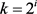 ,i是自然数且
,i是自然数且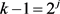 ,j是自然数。又
,j是自然数。又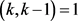 ,可以得到
,可以得到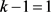 ,即
,即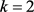 ,与D非平凡矛盾。故而
,与D非平凡矛盾。故而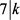 或者
或者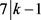 。
。
若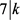 ,则k = 7,显然
,则k = 7,显然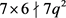 。得出矛盾。
。得出矛盾。
若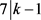 ,则k = 8。当q = 8时,v = 65,r = 64,b = 520。接下来利用Magma [11] 验证存在参数组为(56, 65, 520, 64, 8, 7)的设计。
,则k = 8。当q = 8时,v = 65,r = 64,b = 520。接下来利用Magma [11] 验证存在参数组为(56, 65, 520, 64, 8, 7)的设计。
利用指令Primitive Group (65, 3)可返回本原群库中作用在65个点上排在第3个位置的本原群,即Sz(q)。
由于G是旗传递的,则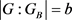 ,故必存在指数为b的子群。利用指令Subgroups (G: Order Equal: = n),其中
,故必存在指数为b的子群。利用指令Subgroups (G: Order Equal: = n),其中 ,可得到G的指数为b的子群,符合条件的子群又1个,即为
,可得到G的指数为b的子群,符合条件的子群又1个,即为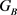 。
。
由于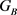 在B上是点传递的,则
在B上是点传递的,则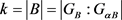 ,则
,则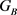 中至少存在一个长度为k的轨道。利用指令
中至少存在一个长度为k的轨道。利用指令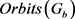 可知有1个长度为k即8的轨道,记这个轨道为
可知有1个长度为k即8的轨道,记这个轨道为
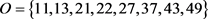 。
。
由于G在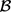 上是区传递的,对于
上是区传递的,对于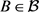 必有
必有 。利用指令
。利用指令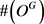 可知轨道O符合条件。利用指令
可知轨道O符合条件。利用指令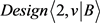 ,返回(65, 8, 7)。可知参数组(56, 65, 520, 64, 8, 7)是我们要找的符合条件的参数。
,返回(65, 8, 7)。可知参数组(56, 65, 520, 64, 8, 7)是我们要找的符合条件的参数。
其次,设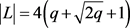 。则
。则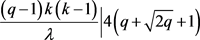 ,可以得到
,可以得到
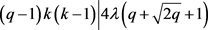
当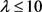 且
且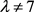 时,
时,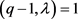 ,可得
,可得
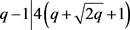
此时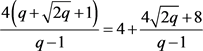 ,因此
,因此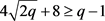 ,可得
,可得 ,故q = 8,32。当q = 8时,
,故q = 8,32。当q = 8时,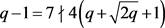 。当q = 32时,
。当q = 32时,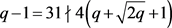 。存在矛盾。
。存在矛盾。
当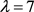 时,若
时,若 ,则可得出矛盾。若
,则可得出矛盾。若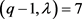 ,则
,则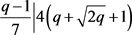 ,此时
,此时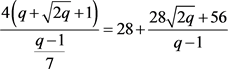 ,因此
,因此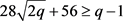 ,可得
,可得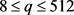 ,得到q = 8,32,512,在这三种情况下均可得到
,得到q = 8,32,512,在这三种情况下均可得到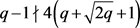 ,得出矛盾。
,得出矛盾。
第三,设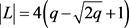 ,则可以得到
,则可以得到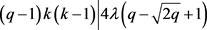 。
。
当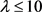 且
且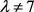 时,
时,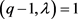 ,可得
,可得 。此时
。此时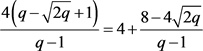 ,因此
,因此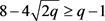 ,可得
,可得 ,不存在正解,得出矛盾。
,不存在正解,得出矛盾。
当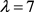 时,若
时,若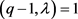 ,则可得出矛盾。若
,则可得出矛盾。若 ,则
,则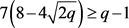 ,不存在正解,得出矛盾。
,不存在正解,得出矛盾。
最后,设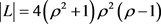 。则可以得到
。则可以得到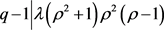 。
。
当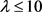 且
且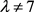 时,
时,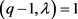 ,可得
,可得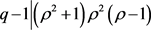 。此时
。此时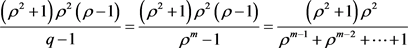 ,故。又,得到
,故。又,得到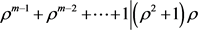 ,推出m = 3。事实上
,推出m = 3。事实上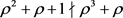 ,得出矛盾。
,得出矛盾。
当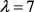 时,若
时,若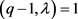 ,则可得出矛盾。若
,则可得出矛盾。若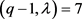 ,则
,则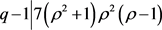 。
。 又
又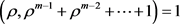 ,得到
,得到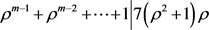 ,事实上得到
,事实上得到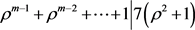 ,推出m = 3。但是
,推出m = 3。但是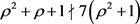 ,得出矛盾。
,得出矛盾。
引理6: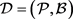 是一个满足
是一个满足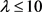 的
的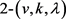 设计,
设计,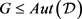 是旗传递、点本原的群,且
是旗传递、点本原的群,且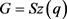 。则
。则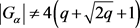 。
。
证明:假设存在点稳定子群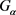 使得
使得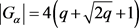 ,已知
,已知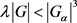 ,即
,即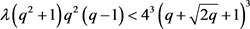 。又
。又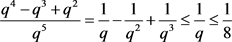 则
则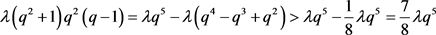 。
。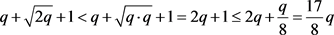 。则
。则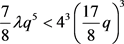 。即
。即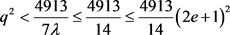 ,得出
,得出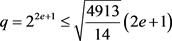 。故q = 8,32。
。故q = 8,32。
当 时,
时,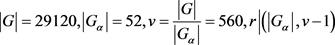 即
即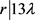 。
。
若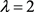 ,则
,则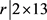 ,故r = 13,26。已知
,故r = 13,26。已知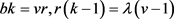 ,可以算出b不是整数,得出矛盾。
,可以算出b不是整数,得出矛盾。
若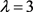 ,则
,则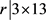 ,故r = 13,39。若r = 39,可以算出b不是整数。若r = 13,则
,故r = 13,39。若r = 39,可以算出b不是整数。若r = 13,则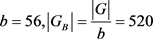
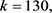 。而G的极大子群的阶只能为448,52或20。并且G是旗传递的,与
。而G的极大子群的阶只能为448,52或20。并且G是旗传递的,与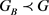 矛盾。
矛盾。
若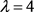 ,则
,则 ,故r = 13,26,52。若r = 13,26,可以算出b不是整数。若r = 52,可以算出k不是整数,得出矛盾。
,故r = 13,26,52。若r = 13,26,可以算出b不是整数。若r = 52,可以算出k不是整数,得出矛盾。
若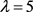 ,则
,则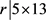 ,故r = 13,65。若r = 65,可以算出b不是整数。若r = 13,则
,故r = 13,65。若r = 65,可以算出b不是整数。若r = 13,则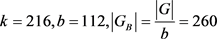 。由
。由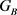 在B上传递可知
在B上传递可知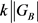 ,但是
,但是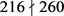 。得出矛盾。
。得出矛盾。
若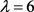 ,则
,则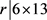 ,故r = 13,26,39,78。若r = 13,26,78,可以算出b不是整数。若r = 39,则
,故r = 13,26,39,78。若r = 13,26,78,可以算出b不是整数。若r = 39,则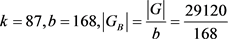 不是整数,矛盾。
不是整数,矛盾。
若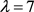 ,则
,则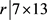 ,故r = 13,91。可以算出b不是整数,得出矛盾。
,故r = 13,91。可以算出b不是整数,得出矛盾。
若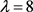 ,则
,则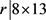 ,故r = 13,26,52,104。可以算出b不是整数,得出矛盾。
,故r = 13,26,52,104。可以算出b不是整数,得出矛盾。
若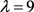 ,则
,则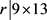 ,故r = 13,39,117。可以算出b不是整数,得出矛盾。
,故r = 13,39,117。可以算出b不是整数,得出矛盾。
若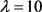 ,则
,则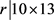 ,故r = 13,26,65,130。可以算出b不是整数,得出矛盾。
,故r = 13,26,65,130。可以算出b不是整数,得出矛盾。
当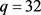 时,
时,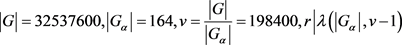 ,即
,即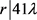 。
。
通过计算可得,当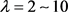 时,b均不是整数,得出矛盾。
时,b均不是整数,得出矛盾。
引理7: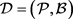 是一个满足
是一个满足 的
的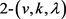 设计,
设计,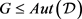 是旗传递、点本原的群,且
是旗传递、点本原的群,且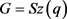 。则
。则 。
。
证明:假设存在点稳定子群 使得
使得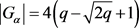 ,已知
,已知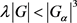 ,即
,即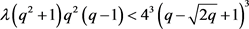 。仿照上一引理可得
。仿照上一引理可得
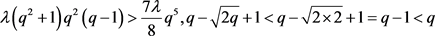 。
。
故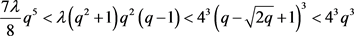 ,由
,由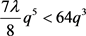 ,可以得到
,可以得到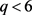 ,与
,与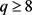 矛盾。
矛盾。
引理8: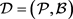 是一个满足
是一个满足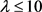 的
的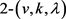 设计,
设计,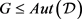 是旗传递、点本原的群,且
是旗传递、点本原的群,且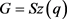 。则
。则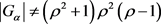 。
。
证明:假设存在点稳定子群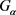 使得
使得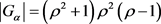 ,则
,则
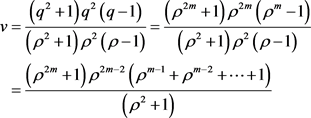
由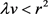 得出
得出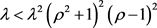 。则
。则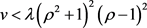 。
。
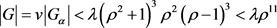 ,又
,又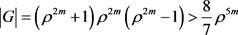 。可知
。可知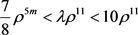 。即
。即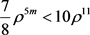 。可以得到
。可以得到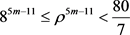 ,从而
,从而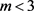 ,得出矛盾。
,得出矛盾。
定理1的证明:利用引理5~引理8可以得到定理1。
致谢
本论文在写作过程中与张志林博士和张永莉博士进行了有益的讨论,在此表示感谢!论文还得到了广东省自然科学基金的资助。
基金项目
广东省自然科学基金(编号:2017A030313001)。