1. 引言
考虑如下的一类三阶半线性中立型时滞微分方程
(E)
的振动性。其中
,
,
为两个正奇整数之比。
假设下列条件成立
(A1)
;
(A2)
;
(A3)
,对每一
,都有
,
按照习惯,方程(E)的解称为振动的,如果它有任意大的零点;否则称其为非振动的.若方程(E)的所有解都是振动的,则称方程(E)是振动的;否则称其为非振动的 [1] 。
文 [2] [3] [4] 对二阶半线性中立型微分方程
(1.1)
做了深入研究,给出一些新的振动准则。最近几年,三阶半线性微分方程的振动性研究开始受到关
注,但是其振动性研究成果还比较少,如文 [1] 、 [5] - [14] 。2017年惠远先等人在限制
的
条件下,建立了保证方程(E)的所有解振动或者收敛到零的若干新的振动准则。
在文 [2] 、 [14] 工作的启发下,应用Riccati变换和经典不等式等技巧,建立了方程(E)在条件
下
的考虑
。情形新的振动性结论,我们的结果推广和改进了
文献中的一些结果,并给出例子说明主要结果的应用性。
2. 引理
引理2.1 [14] 若
是方程(E)的最终正解,则
只有下列两种可能,即存在
,使得当
时,有
引理2.2 [15] 若存在
,
,且
,则
。
引理2.3 [16] 设
,则对任一
,存在
,使得
引理2.4 [6] 设
,则存在
和
,使得
引理2.5 [14] 设
是方程(E)的最终正解,且
满足(B),若
(2.1)
则
。
3. 主要结果
为了利用Philos型积分平均技巧,为此引用如下一类函数F
令
,
。
称函数
属于F类,记作
,如果
i) 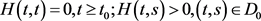
ii) 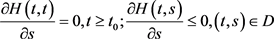
且在D上连续,存在函数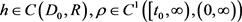 ,满足
,满足
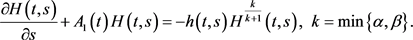
使用记号:对于 ,令
,令
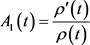 ,
,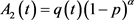 ,
, ,
, ,
,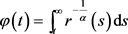 ,
,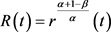 ,
,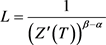 ,
,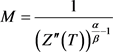 ,T充分大。
,T充分大。
定理3.1 若存在函数 ,满足
,满足 和(2.1)式,且
和(2.1)式,且
 (3.1)
(3.1)
则方程(E)的解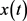 振动,或者当
振动,或者当 时,
时, 。
。
证明 设方程(E)有非振动解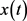 ,由于
,由于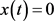 无实际意义,所以我们只考虑
无实际意义,所以我们只考虑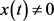 的情形。不失一般性,不妨设
的情形。不失一般性,不妨设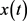 是方程(E)的最终正解,且
是方程(E)的最终正解,且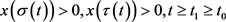 。由引理2.1可知,存在
。由引理2.1可知,存在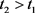 ,使当
,使当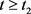 时,
时,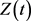 可能为(A)型或(B)型。
可能为(A)型或(B)型。
若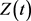 为(A)型,即
为(A)型,即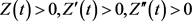 。
。
由于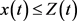 ,所以
,所以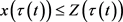 ,于是有
,于是有
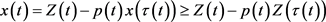
又因为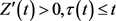 ,所以
,所以 ,从而有
,从而有
 (3.2)
(3.2)
由(3.2)和方程(E)可得
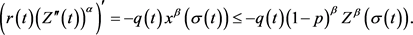 (3.3)
(3.3)
考虑Riccati变换
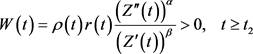 (3.4)
(3.4)
(3.4)式两边对t进行求导,并利用(3.3),(3.4)得
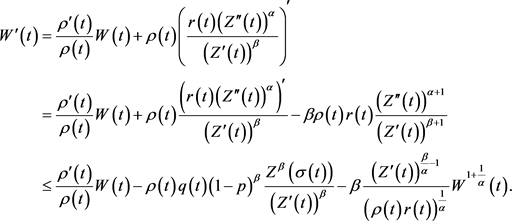 (3.5)
(3.5)
由(A2)可知 ,故易知
,故易知 。
。
由引理2.3,令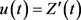 ,对任一
,对任一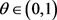 ,存在
,存在 ,使得
,使得
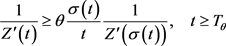 (3.6)
(3.6)
由引理2.4,存在 和
和 ,使得
,使得
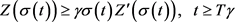 (3.7)
(3.7)
利用引理2.2,取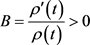 ,
,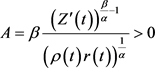 ,
,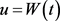 ,
,
则有
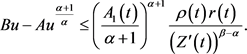 (3.8)
(3.8)
取 ,由于
,由于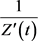 单调递减,所以当
单调递减,所以当 时,有
时,有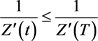 。又因为
。又因为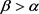 ,于是有
,于是有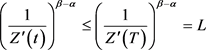 。
。
联结式(3.6),(3.7)和(3.8),有
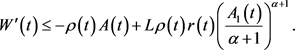 (3.9)
(3.9)
对(3.9)式两边同时从T到t进行积分,得

令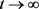 ,根据(3.1)式,则
,根据(3.1)式,则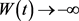 ,这与
,这与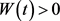 矛盾,故假设不成立,即
矛盾,故假设不成立,即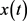 是方程(E)的振动解。
是方程(E)的振动解。
若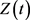 满足(B)型,由于(2.1)式成立,故由引理2.5可得
满足(B)型,由于(2.1)式成立,故由引理2.5可得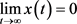 。证毕。
。证毕。
定理3.2若存在函数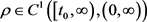 ,使(2.1)式成立,且满足
,使(2.1)式成立,且满足
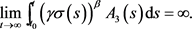 (3.10)
(3.10)
则方程(E)的解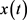 振动,或者当
振动,或者当 时,
时,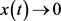 。
。
证明 设方程(E)有非振动解 ,如同定理3.1的证明,若
,如同定理3.1的证明,若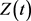 为(A)型,即
为(A)型,即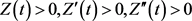 ,则(3.3)式成立,
,则(3.3)式成立,
定义广义Riccati函数
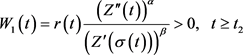 (3.11)
(3.11)
在(3.11)式两边对t进行求导,并利用(3.3)式得
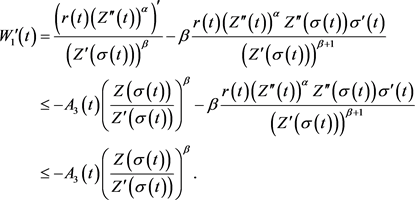 (3.12)
(3.12)
由于 ,于是
,于是 ,
,
取 ,使当
,使当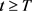 时,(3.12)式变成
时,(3.12)式变成
 (3.13)
(3.13)
对(3.13)式从T到t进行积分得
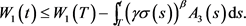
令 ,则
,则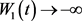 ,这与
,这与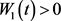 矛盾,故假设不成立,即
矛盾,故假设不成立,即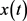 是方程(E)的振动解。
是方程(E)的振动解。
若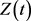 满足(B)型,由于(2.1)式成立,故由引理2.5可得
满足(B)型,由于(2.1)式成立,故由引理2.5可得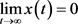 。证毕。
。证毕。
推论3.3若存在函数 和
和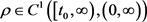 ,使得(2.1)式成立,且满足
,使得(2.1)式成立,且满足
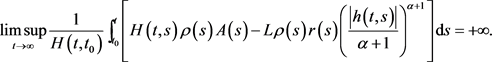 (3.14)
(3.14)
则方程(E)的每一解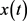 振动,或者当
振动,或者当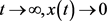 。
。
证明设方程(E)有非振动解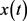 ,如同定理3.1的证明,若
,如同定理3.1的证明,若 为(A)型,定义Riccati变换中的函数
为(A)型,定义Riccati变换中的函数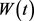 如同(3.4)式,则
如同(3.4)式,则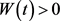 且(3.5)式成立。
且(3.5)式成立。
对(3.5)式两边同时乘以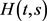 ,并从
,并从 到t积分得
到t积分得
 (3.15)
(3.15)
利用引理2.2,取 ,
,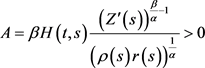 ,
,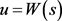 ,且
,且
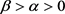 ,故有
,故有
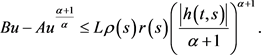 (3.16)
(3.16)
结合(3.15)和(3.16)式得
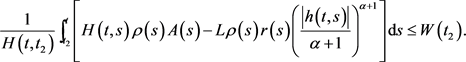
这与(3.14)式矛盾,故假设不成立,即 是方程(E)的振动解。
是方程(E)的振动解。
若 满足(B)型,由于(2. 1)式成立,故由引理2.5可得
满足(B)型,由于(2. 1)式成立,故由引理2.5可得 。证毕。
。证毕。
4. 应用
例 考虑如下的三阶中立型微分方程
 (E1)
(E1)
在这里,我们取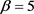 ,
, ,
,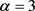 ,
, ,
,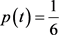 ,
,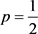 ,
,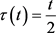 ,
,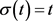 ,
,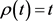 ,由引理3知,当
,由引理3知,当 时,
时,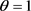 ,
,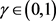 ,
, ,T充分大。
,T充分大。
所以
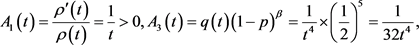
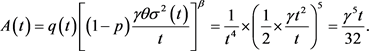
于是有

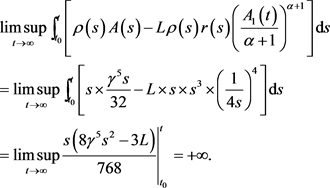
和

显然方程(E1)满足定理3.1的条件(3.1)和(2.1),且满足定理3.2的条件(3.10),即知方程(E1)的解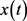 振动,或者当
振动,或者当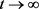 时,
时,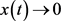 。
。
基金项目
1) 广东省茂名市科技计划项目(2015038);2) 广东石油化工学院理学院科研扶持基金重点项目(KY2018001)。
NOTES
*通讯作者。