1. 前言
《化学键的量子化学研究》这一组四篇文章( [1] [2] [3] 和本篇),是深入探讨化学键本质统一性的。是从Hellman-Feynman静电定理 [4] 的视角:考察化学键各键种以及氢键、范德华作用,都是如何由原子(或基团)对成键区的电子共享产生了结合力、形成化学键的。本文则继续考察金属键和金属晶体、范德华作用和氢键是如何对成键区电子共享产生结合力的,当然没有更多地涉及它们的具体方方面面。
本文的一些约定:
本工作用Gaussian16程序 [5] 进行量子化学计算,各种计算方法会在文中说明,而基组统一用6-311++G**。另外的基组则在文中说明。进一步用GaussView6、Multiwfn 3.1 [6] 进行数据处理和作图。
作电子密度差Δρ时,原子ρ的数据取自Multiwfn程序自带的原子波函数文件。等值线起始值为±0.0004,用几何级数来生成等值线,步长为2,设定等值线条数为20。虚线为ρ减少的区域,实线为ρ增加的区域。此外的数值则在文中说明。
距离不标出单位时是Å,电荷和能量数值不标出单位时是a.u.
2. 金属键与金属晶体
本题着重考察金属键和金属晶体是怎样共享成键区的电子产生化学键的,以及这种电子结构有什么样的特性,从而看到金属键和金属晶体作为一个键种,与共价键、离子键具有共同的本质。并不探讨金属键和金属晶体的其它方方面面的细节。
2.1. 金属键
文献 [7] 综述了金属–金属键化合物的分类及其前景展望。金属–金属键可以是单键,也可以是多重键(2~5重)。金属键是金属之间共享电子形成的共价键。
本节从简单例子的图形来看看它的特色,如何共享又如何离域。
用ccsd方法计算Li-Li得到它的电子密度差Dρ截面等值线图,见图1(A),它完全是一个典型的共价键的电子共享,它类似于图1(B)之H2的Δρ截面等值线,在成键区共享电子。
2.2. 金属键晶体
本小节用B2PLYPD3 [8] 方法进行计算。
计算金属Li的体心立方晶胞。取晶胞的实测参数。
选择金属Li的一个晶胞来计算,它的电子结构及其简单,易于看图说明问题,并且具有金属的典型代表性。金属Li晶胞通常是一个体心立方,见图1(C),实线画出的是晶胞,虚线是在GaussView6中程序判断的成键(原为实线图中改为虚线)。

Figure 1. (A) Δρ of Li2, (B) Δρ of H2, (C) Bcc cell of Li, (D) 5c1e bond of bcc cell of Li
图1. (A) Li2的Δρ,(B) H2的Δρ,(C) Li的bcc晶胞,(D) Li的bcc晶胞的5c1e键
实际上在GaussView,金属晶胞的边楞不再像离子晶体那样可以同时表达原子之间的成键状况,代表键,而是另有成键(见图1(C)虚线所示)。因为从原子距离来看虚线为3.040,实线为3.510。然而这虚线是不是就基本上代表了有这样的成键关系呢?
对Li的体心立方(body centered cubic, bcc)晶胞计算。体心那个Li连有8条“键”(图1(C)虚线)?
从B2PLYPD3计算结果提供的轨道来看,这个晶胞9个价电子,生成了4个双占轨道和一个单占轨道,分别是MO10、11、12、13、14。其中11、12、13正是反映Li晶胞的成键情况的。由于晶胞简单,MO与成键情形恰好对应。11、12、13的能级是简并的、图形是全同的,只是分别放在x、y、z三个轴的方向,从视图看起来是上下、前后、左右。图1(D)是左右方向的MO11,它明确地标示了这是符号相反的两个5中心1电子键(5c1e),符合我们对多中心键的定义 [3] ,这两个5c1e键各有1个电子,而且是相互排斥的。x、y、z三个轴的方向共有6个这样的5c1e键。
图2(A)是MO11的电子密度ρ的中剖图像,这个平面只截到体心原子。电子密度高的是5中心键的中央部分,而不是边楞处。这正是对多中心键的一个判据。多中心共享中央的键电子产生结合力。
在金属Li原子堆砌为晶体时,由于Li之间核与核、电子与电子之间的排斥,Li之间的距离拉得很长,即使是图1(C)虚线所示的距离3.040,也足以使得Li的2s轨道难以参与杂化成键(这在MO中s轨道系数为0可以看出),只有2p型延伸的两瓣能够参与成键,2p的正负两瓣参与形成了正负两个5c1e键,x、y、z三个方向共生成6个5c1e键。图1(C)虚线只是勾画出了5中心键的范畴边楞、轮廓,不再具有单键的含义。
5c1e键是空间立体的,可以想见,这6个5c1e键的电子分布是完全充斥了整个晶胞的空间的。由于这6个5c1e键还是分别共有边楞和面的,能级又是简并相同的,电子在晶胞中融汇成一体可以自由流动。这就是金属晶体电子共享产生结合能的具体情形。这与金属的自由电子模型有相通之处。电子作为波,MO之间是正交的、MO内是分正负的,表达了电子之间的排斥。电子作为粒子,它充满晶胞可以自由流动,而不像共价键拘泥在键的周围、各键各自独立还相互排斥,键之间电子形成节面。
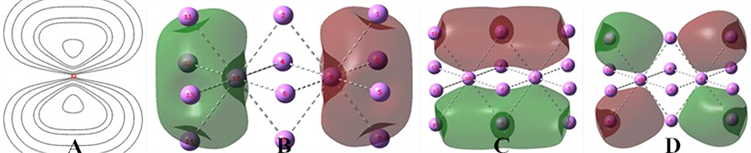
Figure 2. (A) Δρ of 5c1e bond of bcc Li, (B) MO16 5c1e bonds of two bcc cell of Li, (C) MO20 5c1e bonds of two bcc cell of Li, (D)4c0.5e bond in two bcc cell of Li
图2. (A) bcc Li的5c1e键的Δρ,(B) Li的二个bcc晶胞的5c1e键,(C) Li的二个bcc晶胞的5c1e键,(D) Li的二个bcc晶胞的4c0.5e键
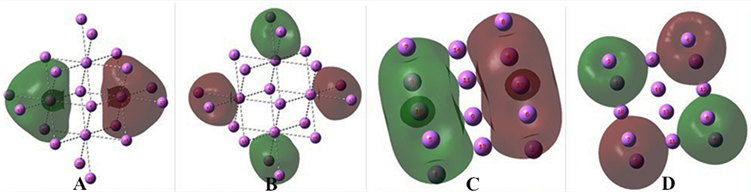
Figure 3. (A) 7c1e bonds of four bcc cell of Li, (B) 3c0.5e bonds of four bcc cell of Li, (C) 9c1e bonds of fcc cell of Li, (D) 4c0.5e bond in fcc cell of Li
图3. (A) Li的bcc四晶胞的7c1e键,(B) Li的bcc四晶胞的3c0.5e键,(C) Li的面心立方晶胞的9c1e键,(D) Li的面心立方晶胞的4c0.5e键
计算连在一起的两个Li体心立方晶胞,它的价电子在各MO形成了多个多中心键。图2(B)是MO16,左右是两个5c1e键,符号相反相斥。图2(C)是MO17,是上下两个5c1e键符号相反相斥。图2(D)是MO20,4个4c0.5e键交互符号相反相斥。
计算连在一起的四个Li的体心立方晶胞,它也是多种多样的多中心键构成的。
图3(A)是MO24的图形,是两个7c1e键反号对峙。7c1e键表达了共享电子的结合,符号相反表达了各键电子排斥。图3(B)是MO26的图形,4个3c0.5e交错反号。
计算金属Li的面心立方(face centered cubic, fcc)晶胞。由B2PLYPD3优化。据计算结果提供的轨道进行分析。它也是多种多样的多中心键构成的。
它的MO16见图3(C)。这是正负两个9c1e键。中间的4个面心原子是共用的。它的MO20见图3(D)。它是4个4c0.5e键交替反号组成的。
计算金属Fe的体心立方晶胞。取晶胞的实测参数。它也是多种多样的多中心键构成的。
它的MO109见图4(A)。它是左右2个5c1e键。它的MO113见图4(B)。它是四个3c0.5e键。
计算金属Fe的面心立方晶胞。取晶胞的实测参数。它也是多种多样的多中心键构成的。
MO174、175、176是三个简并的图形全同的,分别在左右、上下、前后三个方位。每个MO由8个符号相互相反的4c0.25e键组成。图4(C)是MO174,上下两层,是8个4c0.25e键符号相互相反构成的。
图4(D)是MO177,上下各4个4c0.25e键,各键符号相互相反排布。这样的图形组成在前后方位还有MO178、在左右方位还有MO179。

Figure 4. (A) 5c1e bond of bcc cell of Fe, (B) 3c0.5e bonds of bcc cell of Fe, (C) 4c0.25e bonds of fcc cell of Fe, (D) 5c0.25e bond in fcc cell of Fe
图4. (A) Fe的bcc晶胞5c1e键,(B) Fe的bcc晶胞的3c0.5e键,(C) Fe的fcc晶胞的4c0.25e键,(D) Fe的fcc晶胞5c0.25e键
为什么上述金属堆积成的晶体,不能生成一对一的金属键而要生成多中心键呢?以Li为例来分析,Li的价层有4个轨道,只有一个电子,是一个缺电子金属原子。试想如果有Li-Li成键,那么多的空轨道必然会争抢成键的电子。
原子的空轨道并不是真正的空无所有,空轨道表征着一种潜在吸引电子、接受电子成键的能力,以及它的方位、范畴,是作为波的形象,是没有电子占据的客观存在着的核势场、势阱。
Li吸引电子的能力本就很弱,Li堆积成的晶体电子就被众多的空轨道分摊了,从而只能生成多中心键。有的原子提供带电子的轨道,有的原子只提供空轨道,形成多中心键,共享电子。
由于这种多中心键构成的特殊性,在以离域著称的MO中的多中心键,竟基本上是定域的。
在金属晶体,研究晶胞、空间点阵,从而分门别类,这还是必须的,这是数学物理层面的研究,自有它的学科规律性。
只是从量子化学层面看来,金属晶胞构成的晶体的边楞不再可以代表化学键。就是GaussView根据原子间距判断出的键,也不再是真正的键,而是众多多中心键的边楞。
考虑到一些金属团簇,从ELF、定域化轨道等方式考察的时候,可以看到既有多中心作用,也有双中心作用的情况,可以说金属晶体中的键通常具有显著的多中心特征。
3. 范德华作用
范德华作用研究,已经在前文《范德华作用的量子化学研究》 [9] [10] [11] [12] 作了系统的考察。这里只是补充。
3.1. 范德华作用的本质
就像 天然就是可以用来定义多中心键的一个客观实体一样,范德华作用也可以找到这样的客观存在实体,比如He2、Ne2等稀有气体原子二聚体,它们只有范德华作用,没有其它任何键。把它们构成和本质参悟清楚了,也就可以概括、抽象出范德华作用的本质来。
天然就是可以用来定义多中心键的一个客观实体一样,范德华作用也可以找到这样的客观存在实体,比如He2、Ne2等稀有气体原子二聚体,它们只有范德华作用,没有其它任何键。把它们构成和本质参悟清楚了,也就可以概括、抽象出范德华作用的本质来。
用来参悟的第一手原生态信息自然是MO和电子密度ρ的图像,然而范德华作用的数量级如此之小,很难在范德华作用前后MO或者ρ的图像中直接看明白说清楚。这时应该作电子密度差Δρ,即作双方形成范德华作用前后的Δρ,这个Δρ正是范德华作用的唯一具体表现,看见了Δρ就看见了范德华作用本身。
然而Δρ却是“无字天书”啊!这里的“天”,是客观存在的物质世界、天然的化学物质,“书”,是描述天然化学物质性质无文字说明的量子化学图形,如MO、ρ和Δρ。这图形要靠我们的相关知识经验积累来解析。
由于范德华作用的影响如此之小,形成范德华作用双方前后变化甚微,一作Δρ,双方的电子密度没有变化的内容抵消了,Δρ图像展现的只是范德华作用引起的微细的变化。比如Ne2的Δρ,见图5(A)。
我在以前的文章中,提出了范德华作用的新概念 [9]。范德华作用的本质是分子(含原子)的配对电子(包含键电子)之间的作用。
从图5(A)可以清楚地看到,当双方都已是价键完善的配对电子的分子(这里是稀有气体原子)相遇、相碰时,电子云球是塑性的,电子因为相互排斥而变形、相互退让,却使得原子在排斥退让之处电子减少而裸露、电负性升高。电子是灵动地按各处电负性大小作概率出现、分布的,当核的排斥、电子排斥使双方拉开到一定距离(范德华距离)时,排斥减小了,双方比较裸露的核处吸引电子的能力增强却凸显出来了,反而会在双方较裸露的核之间的成键区重新增加电子聚集,形成了分子间电子共享的增加、产生结合力。
图5(A)的黑色线条大致标出了成键区的区划。共享电子又主要布居在二核之间,直接减小了核与核之间的排斥,从而抗衡了双方的配对电子的排斥和核排斥,达到平衡,形成了范德华作用。

Figure 5. (A) Δρ of Ne2, (B) Structure of (CH4)2, (C) Section contours of Δρ of (CH4)2, (D) Δρ of (CH4)2
图5. (A) Ne2的Δρ,(B) (CH4)2的结构,(C) (CH4)2之Δρ的截面等值线,(D) (CH4)2的Δρ
前文 [10] 还对这种分子之间的范德华作用做过扫描(scan),做过扫描全程的Δρ动画。从Δρ动画可以动态地看到,当双方距离在近程、中程时,电子相斥、退让至反键区,较裸露的核排斥、电子排斥使双方核之间电子聚集急剧减少,之间的斥力倍增,双方被拉开。当距离拉开到范德华距离时,相互作用的量变引起质变:双方较裸露的核之间电子聚集却重新增加,共享电子的重新增加形成了对双方核的引力,平衡了双方核与核和电子与电子的斥力,产生范德华作用。再拉开距离,双方核和电子的斥力逐渐减小直至无,核之间电子聚集也恢复常态,双方各自成为自由体了。
这就是两边都是电子配对MO,在对称性允许、不正交时,范德华作用的全过程。虽然历史上学者们是从维系了体系的弱稳定性认识范德华作用的,但如今我们不妨把这全过程都看成范德华作用。只是这作用在近程、中程都是排斥力占上风而已,可以称为范德华作用的排斥阶段。随着双方距离变化,斥力和引力此消彼长。
如果从MO来看这个全过程,发生范德华作用的双方都是电子配对的MO,它们会形成两个轨道安排两对电子:一个MO是同位相的,表达了双方的核吸引电子,包含成键区的共享电子;另一个MO是反相位的,表达了双方毕竟是配对电子,存在Pauli互斥,双方配对电子之间是反键性质的。
总的成键区电子包括Δρ图所示的核间聚集增加的电子和此区未被排斥挤走的剩余电子。从总体看,由于在二Ne之间电子聚集的增加,二Ne的背后远处还是有电子减少,电子向键轴方向浓集了,这些都是共价键的特征,电子共享的特征。如果范德华作用双方的电负性有差别,还会形成电子转移以平衡电负性 [11]。
关于范德华作用的研究,有很多对电子密度作拓扑分析,它们的范德华作用图像,都展现了发生范德华作用的双方之间有共享电子聚集。但这里看不到历来对范德华作用本质猜想的“三种力”的形象。这里并没有一方极化引起另一方的“瞬间偶极矩诱导”。
再看看两个甲烷CH4是如何形成范德华作用的,这个基本无极性的分子对范德华作用是很有代表性的。(CH4)2可以有多个构成范德华作用的方式,这里只以图5(B)这样的构型为例,图5(C)和图5(D)是这种构型的两个互相垂直的截面。用mp4sdq方法计算,作(CH4)2与两个独立的CH4的电子密度差。分别作xy和xz的截面等值线图,等值线的起始值为±0.0000001。
图5(C)为xy截面图,截取了双方两个CH2分子片。这两个CH2分子片由于配对的键电子的排斥,二者中间电子密度大大减少了,转移到两个CH2分子片的背后了。由于这种电子向背后转移,C、C面对面处因电子减少而裸露电负性增加,电子在此处却是聚集增加的。这是在分析问题时分步这么说的,实际上C、C面对面处是随着电子转移到背后、而且双方相距在范德华距离的同时在增加的。这种增加正在C、C的成键区,加上中间排斥的电子密度减少区仍然有一定的电子,此处电子密度减少的梯级也可以看成是电子存在的梯级,它们共同构成了成键区的电子,因为共享成键区的电子,产生了微弱的范德华作用。
图5(D)为xz截面图,截取了双方另外两个CH2分子片。这两个CH2分子片由于配对的键电子的排斥,二者中间电子密度大大减少了,转移到两个CH2分子片的背后了。由于这种电子向背后转移,C、C面对面处因电子减少而裸露电负性增加,电子在此处却是聚集增加的,这种增加正在C、C的成键区。同样还要加上中间排斥的电子密度减少区仍然有一定的电子,此处电子密度减少的梯级也可以看成是电子存在的梯级。图5(D)截面还表明,在两对H……H之间,它们一方面也是因电子排斥电子移动向CH2分子片外,如果对H……H划出成键区,这些向外移动的电子却在成键区也构成了范德华作用。H……H的距离为2.9743,正是范德华作用的距离。C……C相距4.2260,也还在范德华作用的距离范畴。
实际情形不仅是这样一一对应地共享电子产生范德华作用,而是这方CH2分子片与对方的CH2分子片共同吸引成键区的共享电子形成范德华作用。
3.2. 范德华作用的存在范畴
当涉及到分子间的相互作用,如范德华作用、氢键时,我们不妨说范德华作用是长程的,长度数量级约在3~4或者更长;说氢键是中程的,长度数量级约在2左右或者更长(在氢键通式X-H⋯Y中H⋯Y的距离);一个原子上相邻两个键是近程的,长度数量级约在1.5左右或者更长。
说到这里,不禁会产生一个疑问:范德华作用,为什么只在长程才有作用?为什么一种作用在长程时已经显现出来,而中、近程反而不见了?这似乎不合逻辑!
这是因为作为配对电子之间的作用,历史上是从结合力的方面发现范德华作用的,这时是长程的。而在中、近程,配对电子之间的作用是排斥占上风的,表现为斥力。
既然说范德华作用是分子(含原子)的配对电子(包含键电子)之间的作用,其实,无论分子间,分子内,原子内,配对的电子之间都是存在这种范德华作用的。
配对电子之间的近程范德华作用,可以在氢键体系中存在 [13]。分子间形成氢键时,它同时拉拢、锚定了对称性允许、不正交的双方MO,双方都是电子配对的MO,它们会分别形成两个轨道安排两对电子,一个MO是同相位的,表达双方核对电子的引力,另一个MO是反相位的,表达双方配对电子的斥力。这些就是所谓“氢键相关MO”。在一个氢键体系可以有几组这样的MO。
现在考察一下分子内相邻两键的近程相互作用,配对的键电子之间的作用实际上也属于范德华作用。至于这种作用属于范德华作用的什么阶段,是范德华作用的排斥还是吸引,这要根据具体情况来分析。
可以设计许多邻键小分子来看一看,如H2O、H2Be。
H2O,两个OH键构成了双方配对电子的范德华作用,有一个MO表明两个OH是同相位的(各核吸引电子),另一个MO是反相位的(电子之间的排斥),从O的两个(与H成键的)单电子看,它们本是互成90˚的,但由于键电子之间的相互排斥,键角增大了,可是又受到O的孤对电子排斥的制约,实验结果键角是104.5˚。
H2Be,两个HBe键相互排斥,而这里没有孤对电子排斥的制约,键角达到了180˚。
上述配对电子的情况,都是键上的共享电子处于电负性高或较高的原子之间,键电子之间排斥作用占上风,电子基本被束缚在键上(成键区里)不易变形,属于范德华作用的排斥阶段,大多数分子属于这种状况。键电子之间的相互作用构成了键角,影响键长,决定了杂化。
4. 氢键
关于氢键的研究,已经在前文《氢键的量子化学研究》 [13] [14] 作了系统的考察。这里只做补充。
在氢键通式X-H⋯Y中,历来设想氢键是带部分正电荷的H分别吸引带部分负电荷的X和Y所形成的纯粹的静电吸引作用,但实际上这种设想并不成立,为什么呢?为什么需要建立氢键新概念?
还是通过一个氢键实例(HF)2来看一看。由于(HF)2的氢键对其中两个HF的影响甚弱,氢键中的HF基本保留着它在自由态的基本性质。强极性键HF成键的Δρ,见图6(A),这里H与F形成了强极性共价键,从H转移到F(通式中的X)的电子就是F的所谓负电荷,这个负电荷安排在反键区,这负电荷在键的外端吸引F,起着拉开键的作用,并不会与H产生所谓纯粹的静电作用的氢键引力。
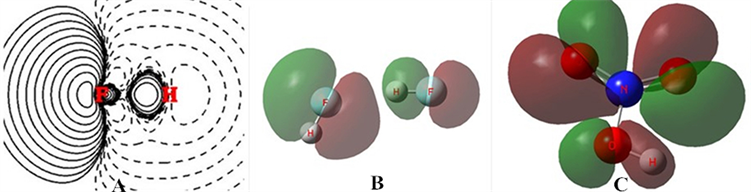
Figure 6. (A) Δρ of HF, (B), MO8 of (HF)2, (C) MO16 of HONO2
图6. (A) HF的Δρ,(B) (HF)2的MO8,(C) HOO2的MO16
再看另一个F (通式中的Y),它也是在它的HF中得到负电荷的,这个在端头的负电荷是否会形成纯粹的静电作用吸引另一个HF中带正电荷的H呢?但是纵观所有的Y,其上既有端头的负电荷,又有孤对电子n,这二者在空间排布上是相互垂直的、它们的MO是正交的。但形成氢键时总不是端头的负电荷直对着H-X,尽管这时基本上呈现直线型,纯粹的静电作用最直接、键电子间排斥最小,然而事实上总是孤对电子n直对着H-X。而在HF中,端头的负电荷所在的MO比孤对电子n的MO能级低得多,n更易给出。这里,预示着不是纯粹的静电作用,而会是另有机理。
实际上当氢键形成时,氢键形成了一个新的客观存在,有一个MO专门反映这种新的存在,见图6(B)。
我曾经提出了氢键的新概念 [13] ,它总地可以表述为:氢键是分子内、分子间处于能级较高部位的电子(如HOMO),在轨道对称性相符、不正交时,向能级较低的空位(如LUMO)的势阱偏移了部分电子,形成了双方共享电子、能量降低的较稳定的静电作用体系。说能级较高部位的电子向能级较低空位偏移部分电子,把锂键、钠键、卤键、双氢键等都包含了。在人所共知的氢键通式X-H⋯Y中,是Y的电子部分偏移到X上了,能量有所降低,在成键区形成了X与Y的电子共享。
从MO看,分子间形成氢键时,会形成一个Y的部分电子偏移到X上的氢键MO,它是由Y的孤对电子或单电子延伸、部分转移至X处的空轨势阱形成的。
在氢键体系,同时还伴随有几对MO被说成是“氢键相关MO”。这是当形成氢键时,它同时会拉拢、锚定了对称性允许不正交的双方几对MO,这时双方都是电子配对的MO,它们会分别形成两个轨道安排两对电子,一个MO是同相位的,表达双方核吸引电子潜在的引力,另一个MO是反相位的,表达双方的电子斥力。这是伴随着氢键生成而存在于氢键系统内部的范德华作用。
在氢键通式X-H⋯Y中,氢键新概念的要点是:Y在成键中接受了较多的电子使得其上孤对电子n处于能级高位,常是HOMO。这时孤对电子的部分电子转移地只能是X-H相应的LUMO(或者更高),因为其它的MO都是电子满占配对成键了的。这LUMO是反键轨道,分离出X的p型轨道和H的s轨道是反相位对峙的。n是p型轨道,当它部分转移过来时与H的s轨道相位不符,只能舍近求远地落在X的对称性相符的p型空轨道上。分子内氢键HONO2同样符合上述要点,氢键轨道是MO16,见图6(C)。它也是O上的孤对电子向HO中O的空轨道转移电子。
然而LUMO的能级远比HOMO还高,为什么氢键总是自动生成的呢?其实,LUMO的能级计算值是设想有一个电子占据这个空轨道时的值,作为一个真正的空轨道,它的能级值在没有电子占据时是远低于对应n的计算值的,是X-H外围的一个势阱,随着落入的电子增多能级逐渐升高,落入一个电子时才是LUMO的能级值。而氢键电子转移量通常较小,只是到双方电负性(或说是能级)均衡即止。
当氢键体系又与外面的电子给体构成另外的氢键时,它的通式可写成Z ≈ X-H⋯Y,可以解释所谓氢键蓝移的种种情形 [14]。
氢键构成的成键区的电子共享,就是Y的孤对电子母体p型轨道属于成键区的部分和落入X势阱中转移电子的子体p型轨道属于成键区的部分,它们受到X和Y的吸引、共享。这是核对电子的吸引。而这母体平移部分的子体过去,母体与子体的p型之间却是反相位相邻、衔接的,见图6(B)。原本这个LUMO就是反相位的,现在继承了下来,这是两部分电子之间的排斥。对立的统一。
这个格局之中,H对称性不相符并没有参与组成氢键MO,H只是通过与X定位,让X的LUMO的p型轨道取向与Y的HOMO的p型轨道空间取向的对称性基本相符。
5. 结论
金属晶体主要是以多中心键的形式共享电子产生结合力的。
总结《化学键的量子化学研究》 [1] [2] [3] 和本篇这四篇文章,化学键(共价键、离子键、金属键、多中心键等)、化学作用(氢键、范德华作用等),它们具有统一的本质,那就是原子之间对成键区的电子共享,共享电子同时吸引着各个原子,克服了各原子之间的核与核的排斥和电子与电子的排斥,达到吸引和排斥的稳定平衡,形成了化学键,稳定了体系,构成了化学物质世界。
当代的化学应用,器件越来越小,已经到了纳米的数量级,化学键、化学作用的研究也日益追随到了这样的微观数量级。正确把握化学键、化学作用本质的共性和个性,扬弃不符合客观存在的种种猜想,用量子化学正确模拟微观化学键和相互作用,对计算结果进行化学键的正确分析理解,对研究化学体系的结合、结构和性质至关重要。
致谢
本文的计算由北京科音自然科学研究中心的卢天博士提供计算资源,并对此研究工作进行了讨论,特此致谢!