1. 研究内容与研究方法
1.1. 研究内容
论文在学习配送中心相关基础概念,回顾选址问题发展历程,与模拟植物生长算法及其应用等研究基础上分析了S公司配送中心选址问题的属性。将问题抽象为一个多目标规划的韦伯型多设施选址问题,结合指标选取原则建立了S公司配送中心选址指标体系,并给出了求解指标权重的具体方法。最后为求解所建选址模型,设计了改进后的模拟植物生长算法,利用计算所得数据在MATLAB中编程求得S公司配送中心选址地点的坐标位置。最后通过卫星地图定位分析所得地点在地理环境上的建址可行性。本论文主要研究以下几个方面:
1) 学习配送中心相关基础概念,总结选址问题发展历程与经典模型。
2) 在分析S公司配送中心选址问题的基础上引出其本质——多设施韦伯问题。
3) 构建S公司配送中心选址问题的模型,详细介绍选址原则、模型的建立、评价指标体系的建立及其权重的确定以及华东地区各目标坐标点的转换。
4) 分析现有求解方法的局限性和模拟植物生长算法解决本文问题的适用性,根据模拟植物生长算法不足之处提出改进方法,并通过算例进行改进后算法有效性的验证。
1.2. 研究方法
本文运用数学建模的思想,将S公司配送中心的选址问题抽象为韦伯型多设施选址问题,为确定各点权重值建立了相应的评价指标体系,主要采用的研究方法如下:
文献资料法
通过阅读相关资料及国内外文献,了解现有配送中心选址模型与解决方法,学习现代启发式算法,研究新兴模拟植物生长算法的前沿理论,掌握应用和改进模拟植物生长算法的具体思路和方法。在此基础上,认真思考影响S公司配送中心选址的现实因素,设计应用于S公司配送中心选址的数学模型和求解的改进模拟植物生长算法。
定性分析与定量分析相结合
定性分析是将研究对象的特性进行归纳和演绎、分析与综合以及抽象与概括;而定量分析主要是针对研究对象进行具体量化的分析。本文对配送中心主要功能、特性、影响选址的评价指标等采用定性分析的方法,在此基础上建立了定量的选址模型,并使用模拟植物生长算法在MATLAB中编程求解。
数学建模与仿真计算相结合
本文构建了配送中心选址的数学模型,介绍了基于模拟植物生长算法的求解过程,将其运用到S公司华东地区配送中心选址的问题中,对所建模型的实用性进行了实证检验,得到了较为理想的效果。
1.3. 论文创新点
1) 本文在建立S公司配送中心选址模型时考虑了各配送中心之间的“排斥作用”,建立的模型是一个包含总权重距离最小和各配送中心间距离最大的多目标规划模型,区别于传统的多设施连续选址模型,使模型更具有实际应用意义。
2) 本文针对模拟植物生长算法新枝生长方向单一的问题,将原有算法中的固定生长角度改进为可变角度,从而提高算法收敛速度和寻优能力。
2. S公司配送中心选址模型建立
2.1. S公司配送中心选址问题描述
S公司是由世界500强、全球办公服务行业领袖企业——美国STAPLES公司在中国投资成立的外商独资企业。美国STAPLES公司是全球卓越的办公用品公司,可根据客户的需求来提供一站式办公用品采购服务,公司成立于1986年,总部位于美国马萨诸塞州的波士顿。目前S公司在全球拥有2100余家办公用品超市和仓储分销中心,全球员工总数超79000名,业务涉及20多个国家和地区。2004年,S公司来到中国在始终坚持其经营理念“Make It Easy”的基础上结合我国市场特点丰富了其服务内容。公司主营商用设备、电子数码、日用百货、办公文仪、家居礼品共五大类数万种办公用品。S公司的经营模式分为自营与外包两类。其中自营地区所涉及的商品配送服务由S公司自有物流或是供应商提供。S公司在华东地区现有的配送中心位于上海市松江区,主要负责上海、浙江和江苏三个地区的商品配送服务。随着S公司近年来一直积极推进“互联网+”政企采购平台电商化进程,公司业务范围不断扩大,与诸如中国移动、中国联通、国家电网等大客户达成长期合作计划,松江仓目前已远远无法满足S公司现有业务量:2017年11月单月销售额创历史新高,较原有记录增长143%;2017年12月8日单日销售额创历史新高,较原有记录增长159%;2017年全年销售额同比增长超55%。业务量的急剧增加导致松江仓屡次出现爆仓现象,严重影响了公司口碑及客户满意度。因此,针对当前国内特别是华东地区高速发展的业务需求,相对短缺的供给状况,公司决策层针计划在江浙沪地区建立新的配送中心,以提升物流效率,更好的实现公司“三天必达”的服务承诺,挖掘市场潜力,抢占市场份额。
若将S公司配送中心规划在规定服务区域内的某些地点,由于受客户需求、交通条件、成本等因素的影响,公司整体物流系统的运营成本会由于布局方案的不同而产生非常大的差距。因此,S公司配送中心选址问题的关键在于如何在其服务区域内找到合理的地点作为建址点。为体现整个物流系统的成本最低,可通过令各配送中心到各目标服务点的总权重距离最短来反应。为了方便计算,在研究过程中我们可以用区域内的某个固定点来代表实际服务区域内的目标服务点。故此,研究所需要解决的问题即转化为找到区域点若干个到已知目标服务点的总权重距离最短的点——即将S公司配送中心选址问题简化为经典的多设施韦伯问题(MWP)。在此基础上,考虑到配送中心整体布局的合理性,所建各配送中心之间应存在“排斥”作用:即在满足总权重距离最小的同时,应当使各配送中心之间尽量远离。
2.2. 模型的建立
为构建出S公司配送中心选址问题的模型,我们需要做以下假设:
① 每个目标点客户需求一定,不随时间大幅波动;
② 所有运输路径上运输速度恒定,为同一常数;
③ 各配送中心到各目标服务点的距离可近似为直线距离;
④ 各配送中心不存在同时断货情况;
⑤ 各配送中心有足够的配送能力,可一次性配送完成客户所需物品;
⑥ 各配送中心均以相同概率为所有客户提供配送服务。
在上述假设基础上,我们可以在配送区域内设共有n个目标服务点
,第i个目标服务点到第j个配送中心Pj的距离为
,拟建立m个配送中心P,使其到各带有权重的目标服务点的总距离最短,且各配送中心之间距离尽可能大,表示为式1:
(1)
其中,U表示配送中心到各目标服务点的加权距离之和;Dj表示待定的第j个配送中心到全局最优点配送中心之间的距离;Djk表示待定的第k个配送中心到待定的第j个配送中心之间的距离,且j > k;
为各客户需求点按指标体系进行赋权之后的权重,具体指标体系在3.3节内容中介绍;从式3-1中可知,需解决的目标函数的数量与实际案例中S公司拟建立的配送中心数量m有关:当m = 1时,模型简化为求minU的单一设施选址问题,即经典的Steiner问题模型;当m = 2时,模型简化为求minU和maxDj两个目标函数。
从该多目标规划模型可以看出,在得到全局最优解后的决策目标是使下一个选址地点在满足到各目标服务点的权重距离最小的同时离全局最优解的距离最远,且满足已选出的选址地点两两之间的距离最大。
2.3. 算法选择
2.3.1. 现有方法的局限性
为解决上文所提出的多设施韦伯问题,一般可采用诸如Cooper算法、Cooper-NB算法等方法。但这些方法在应用于现实案例时,均存在一定的问题:若某一目标服务点所在位置与某次迭代所得结果恰巧重合时,使用Weiszfeld程序与NB方法所得的下一步迭代无意义。而利用诸如模拟退火法、蚁群算法和遗传算法等智能算法来解决类似问题时需要确定例如衰减因子、交叉率、变异率、惩罚系数等直接影响算法收敛性和计算结果的参数,如何设定恰当的参数本身就是一个难题。若使用重心法则难以解决各配送中心提供不同服务的多点选址问题:从纯数学角度考虑,将所有待选点均集中在重心处可使权重距离最小,但在实际应用中,应考虑配送中心之间的“排斥”作用,优先选择就近的配送中心提供服务,配送中心之间应尽可能的远离,根据重要程度将各个配送中心分别安排在最优解和次优解才能保证布局的合理性。
2.3.2. 模拟植物生长算法对该问题的适用性
通过上述分析可看出本文的选址过程对于所用算法能否得到精确的局部最优解的要求很高,而模拟植物生长算法能同时得出一个最优点和若干个有效次优点,这一特点非常适用于S公司配送中心选址问题的求解。李彤,陈畴镛对模拟植物生长算法做出如下概括:模拟植物生长算法从理论分析和算例结果的角度来说,具有以下遗传算法、蚁群算法和模拟退火算法等其他的智能算法所不具备的优点:① 模拟植物生长算法在求解时有较强的稳定性,且由于PGSA不将约束条件和目标函数同时进行处理,并且不涉及解码和编码等复杂的处理方式和构造新的目标函数,也不存在交叉率、惩罚系数、变异率选取等问题,使得算法实现相对简单;② 模拟植物生长算法的搜索机制是基于生长点形态素浓度所决定的随机性和方向性平衡,能以较快的速度搜索出全局最优解 [1] 。综上所述,本文决定使用PGSA对研究问题进行求解。
2.4. 坐标转换
解决S公司配送中心选址的首要工作就是确定各个目标服务点的具体方位坐标。利用PGSA求解韦伯型多设施选址问题时使用的坐标数据是平面坐标系,而WGS-84坐标系才是如今的地理信息系统中通常使用的。由于WGS-84坐标系无法直接在本文中使用,所以在计算时需对坐标系进行转换。
WGS-84坐标是一种地固坐标系:采用WGS-84椭球,坐标原点为地球质心,X轴指向BIH1984.0零度子午面和CTP赤道的交点,Z轴指向BIH1984.0定义的协议地球极CTP方向,Y轴和Z、X轴构成右手坐标系 [2] 。
为解决本文的选址问题,计算时将WGS-84坐标转化为高斯平面坐标的具体步骤如下:以WGS-84的参考椭球为基准将WGS-84大地经纬度进行高斯投影后,将高斯投影后的平面坐标与WGS-84坐标系中的坐标进行强制统一(通过如仿射变换、完整二次多项式变换等平面坐标强制转换的方法实现),以完成对应坐标匹配。文献 [3] 给出了投影变换的方式:
(2)
(3)
式2与式3中:
X代表从赤道到B维度的子午线弧长;
为辅助变量;
为卯酉圈曲率半径;
为第二偏心率平方;
为辅助变量;
为椭球点经度与相应中央子午线的差值;
a,b分别为参考椭球的长短半径。
上述的高斯正算公式实质是舍去其6次以上高次项,舍去子午线的弧长计算式8次以上高次项之后的泰勒级数的展开式。通过上式所得坐标可精确至0.001 m。将通过WSG-84坐标转化所得的平面坐标进行计算,再将所得选址点的平面坐标转换为空间经纬坐标。
3. 模拟植物生长
3.1. 模拟植物的生长演绎方式
L-系统遵循局部决定系统的生长法则,每个单元的行为只与它周围的单元行为有关,每个单元的无意识行为造成了整体系统的涌现。对植物生长做形式化的描述,可以根据以下几点进行 [4] :1) 破土而出的茎杆在一些叫做节的部位长出新枝;2) 大多数新枝上又长出更新的枝,这种分枝行为反复进行;3) 不同的枝彼此有相似性,整个植物有自相似结构。
根据单个单元与周围单元的联系度,L-系统可分为“与上下文无关”和“与上下文有关”两种。由于“与上下文无关”的L-系统的重写规则只对单个字符串有效,系统可以无限制生长;“与上下文相关”的L-系统只有当单个字符遇到特定的邻居字符时,重写规则才起作用。为了便于理解,本节在一个特殊的L-系统-OL-系统中演示生成一束分枝的过程,用“()”表示分枝向左生长,用“[]”表示分枝向右生长,生长规则如下:
1:a → c[b]d;2:b → a; 3:c → c;4:d → c(e)a;5:e → d
图1为OL-系统中一个分枝的生长过程,这个过程的生长过程规则如表1所示。

Figure 1. Growth of a branch in an OL-system
图1. OL-系统中一个分枝的生长过程
3.2. 模拟植物生长算法
文献 [5] 对模拟植物向光性的概率生长模型进行了研究分析,并提出了求解茎、枝上形态素浓度的计算方法。设长度为M的树干上有t个生长点,则
对应生长点的形态素浓度为
;同样,设单位长度为m的树枝上有k个生长点
,对应的形态素浓度为
则茎、枝上的生长点形态素浓度值分别如公式(1)、(2)所示:
(4)
(5)
其中,S0为初始可行解,(及种子,初始生长点);f(*)为生长点的背光函数。式(4),式(5)抽象概括了生长点形态浓度与光照环境的对应关系,表明各生长点形态素浓批度取决于各点相对于树根的相对位置及该位置的环境信息。通过上式,可知所有生长点的形态素浓度值为1,即
(6)
在确定了形态素浓度之后,就可以建立植物的向光性机制,即形态素浓度较高的生长点(细胞),将具有较大的优先生长机会,其算法可描述为:设在树干和树枝上共有t + k个生长点,
,按照公式(4)与(5)分别计算其形态素浓度值为
,公式(6)已经证明了,
,因此其空间状态如图2所示。计算机系统不断产生新的随机数,这些随机数就会向[0, 1]区间内不断投掷小球,小球落到
的某一生长状态空间内,所对应的生长点就能得到生长的权力。长出新的长出新的茎、枝,相应的t,k值也进行调整,新生的茎、枝的生长点作为新的生长点加入到下一轮选拔的过程,直至没有新枝出现为止,最终成为一株植物。

Figure 2. State space of Morphin concentration
图2. 形态素浓度状态空间
4. 模拟植物生长算法的改进
4.1. 初始生长点的确定
利用模拟植物生长算法解决问题的第一步便是设置模拟植物的初始生长点,原算法采用的是随机生成初始生长点。但随机生成的初始生长点不仅对模拟植物的初期生长有影响,而且还会影响到算法迭代中新生长点的选取及其函数值,这对算法的演算效率有着严重的负面影响。为了降低初始生长点对模拟植物生长算法计算效率的影响,首先需解决的问题就是尽量减少人为因素对初始生长点选取的影响。
针对该问题的解决,模拟植物生长算法提出者李彤教授结合分形几何工具引入有限元思想,将初始生长点直接设定在在可行域范围内。通过建立生长点间的拓扑关系来划分初始的可行域空间,使其自动生成出合理的初始生长点网络,从而改进了原始的模拟植物生长算法。Tumer等人于1956年首次提出了有限元思想(FEM),为复杂工程问题的解决提供了巨大的帮助。该思想核心在于通过单元划分将一个整体结构看作一个由有限个单元互相拼接成的几何体 [6] ,且所分单元的细化程度决定了FEM描述下的模型准确程度。由于模拟植物生长算法本质是相对空间的分形点集,因此在选择合理的拓扑结构时将采用分形几何学中的谢尔宾斯基地毯 [7] 。谢尔宾斯基地毯本质特点为:具有处处有洞但连续,面积为0但周长无穷大(图3)。
将谢尔宾斯基地毯作为优化问题的可行域范围,将地毯中各个正方形的顶点作为模拟植物的初始生长点,即有限元网格的结点,但需要注意的是地毯中去除的部分依然需要用相同的规则处理和设定初始生长点。
4.2. 新枝生长方向的确定
原有算法将新枝的生长生长方向定义为东、南、西、北,新枝之间旋转角度为90˚,这样一来使得每一次迭代后树枝仅朝向和坐标轴平行的方向生长,这无疑既不符合真实植物实际的生长过程也将拖慢算法的计算速度。为解决这一问题,本文根据现实世界中新枝生长方向的实际情况,打破固定的生长角度,引入随机选择生长角度,使得算法在求解时可增加搜索范围,以期提高算法运算效率。
4.3. 改进后算法有效性验证
在上节中,讨论模拟植物生长算法存在问题及改进方法,并最终提出两种改进方法,分别为优化初始生长点的设定和新枝生长方向的重新设定。为了方便计算,本节采用将选址模型简化后的算例来验证改进算法的有效性,对比分析改进前后算法的计算效率。
算例:
该算例中,目标函数为
,自变量为
。显然,当
时,目标函数最优解为
,图4为该函数的可行。
利用改进后的PGSA对算例进行代码撰写,对改进后算法的有效性进行验证,设置搜索步长为0.1,迭代次数为1000。如图5到图9所示,其中A曲线表示改进前PGSA的寻优过程,B曲线表示采用谢尔宾斯基直接设定生长点进行生长的寻优曲线,C曲线表示采用直接设定生长点和随机生长角度后的寻优曲线。
分析以上5张图可知,模拟植物生长算法有很强的寻优能力,求解稳定性较好,具体来看:
1) 比较图5到图9的A曲线(改进前的模拟植物生长算法)可以发现原算法对初始生长点的选取有较大的依赖性,若初始生长点的选取靠近最优解,原算法可以较快的找到最优解,否则则会影响算法的求解速度,不利于大规模的计算。
2) 相比于原算法,引入有限元思想,利用谢尔宾斯基地毯直接设定生长点的改进策略使算法收敛速度的稳定性得到了保障,有效避免了由于初始生长点选取不当而造成的算法收敛过慢的现象(B曲线迭代次数均在600次左右),且总能取到最优解,不会产生收敛于局部最优解的现象。

Figure 5. When the random growth point of curve A is (16.5, 14.5)
图5. 当A曲线随机生长点为(16.5, 14.5)时

Figure 6. When the random growth point of curve A is (14.2, 9.0)
图6. 当A曲线随机生长点为(14.2, 9.0)时

Figure 7. When the random growth point of curve A is (−9.0, −10.1)
图7. 当A曲线随机生长点为(−9.0, −10.1)

Figure 8.When the random growth point of curve A is (9.2, −17.6)图8. 当A曲线随机生长点为(9.2, −17.6)时
图8. 当 A 曲线随机生长点为(9.2, −17.6)时
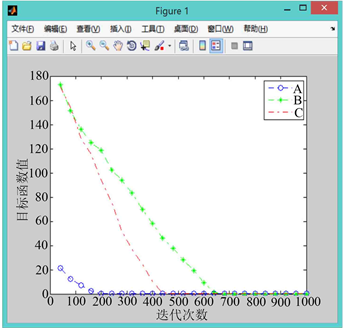
Figure 9. When the random growth point of curve A is (4.3, −3.3)
图9. 当A曲线随机生长点为(4.3, −3.3)时
3) 对比B曲线与C曲线可以看出,同时采用直接设定生长点与采用随机生长角度的改进后算法与原算法相比,收敛速度有了进一步的提升,算法计算效率比仅采用直接设定生长点进行改进的算法提高了30%左右,在保证寻优能力与收敛速度稳定性的基础上增加了运算效率。
综合以上分析我们可以看出本文提出的模拟植物生长算法改进策略均是有效的,在保证算法可求出最优解的基础上能比原有算法拥有更快的巡游速度和收敛稳定性。
4.4. 改进后PGSA的算法步骤与流程
根据本文之前的分析,我们可以定义该问题中模拟植物的自相似结构为:假设从生长点生长的新枝以角度α偏离东、南、西、北这四个方向进行生长,新枝间的角度为90˚,通常情况下,设定新枝生长的长度为L/1000 (L代表目标函数可行域的长度)。
对于n个权重分别为
的需求点
,求m个点Pj使
最小,
与
最大。该问题的改进后PGSA的迭代步骤为:
Step 1:确定h个初始生长点
,X为目标函数的可行域,初始生长点为谢尔宾斯基地毯中正方形的顶点;
Step 2:求解各生长点形态素浓度(生长概率):
(4-4)
Step 3:以Step 2中所得各点的生长概率为标准,构建各个生长点在0~1范围内的概率空间,用随机数来选择本次要迭代的生长点
;
Step 4:确定树枝长度(通常为L/1000,L代表目标函数可行域的长度),生长点
长出新枝后得到新的生长点,通过式4-4得出新生长点的生长概率,选出其中的最优点来替换
;
Step 5:若无新生长点产生如且完成了设定的迭代次数,则停止计算,输出局部最优解和全局最优解,不然转回Step 2。
5. 案例计算
5.1. 研究区域的选取
浙江省、江苏省和上海市是本文中S公司拟建配送中心的服务范围。该地区经济基础雄厚,以2.24%的国土面积占比,贡献了全国GDP总量的19.55% (2017年),且物流业发展始终处于领头羊地位,各大物流公司网点密集。本文根据往年销售数据筛选出8个城市(分别为上海、南京、无锡、苏州、南通、杭州、宁波、台州,销售占比约为86%),并根据S公司管理层的发展意见,选出5个城市(徐州、常州、温州、绍兴、金华)作为未来主要开拓市场,共13个城市作为目标服务城市,利用所建选址模型,综合考虑上文4.3节中建立的评价体系中准则层里潜在客户、投资环境、成本因素三项要素,寻找两个合适的配送中心建址地点。图10为江浙沪地区行政区域图。

Figure 10. Administrative area map of Jiangsu, Zhejiang and Shanghai
图10. 江浙沪地区行政区域地图
5.2. 坐标转换
在Google Earth中抽象出13个目标城市的地理坐标(设中央经线设定为120˚,以13个城市的市政府所在地为代表点,即目标城市政府所在点的经纬度),这13个地理坐标也就是案例中13个需求点的地理坐标。利用3.4节中提及的坐标转换公式进行坐标的转换,如表2所示。图11为Google Earth中需求点坐标的获取情况。

Figure 11. Acquisition of coordinates of each target city in Google Earth (taking Shanghai as an example)
图11. Googel Earth中各目标城市坐标获取(以上海市为例)

Table 2. Coordinates and weights of each target city
表2. 各目标城市坐标及权重
5.3. 模型计算及分析
将平面坐标数据带入模拟植物生长算法的程序中,以
与
两个值之中的最大值作为运行程序中的L (函数可行域),以minU作为唯一目标函数,经过20,000步迭代,得到最优解,即进行单一选址时应选取的地点,坐标为(1151696.7, 3456786.6),目标函数minU最优值为162,666.3。然后进行第二次选址,目标函数为minU与maxDj,即选址地点到各目标服务点间总权重距离最小且满足与最优解之间距离最大的坐标点,部分结果及其对应的多目标函数值如表3所示。

Table 3. Partial local optimal solutions of the second site selection
表3. 第二次选址的部分局部最优解
分析表3中数据可知,若要保证权重距离U较小,则该点距离已确定的最优点的距离Dj也相对较小;若要保证离最优点的距离Dj相对较大,则该点的权重距离U也会相应较大。因此该多目标规划的配送中心选址问题在选址数量为2时不存在全局最优解,所得结果为局部最优解。在二次选址的所得5个局部最优解中进行分析,5个局部最优解的权重距离与已确定的最优解权重距离相比,权重距离分别增加了2616.3、4143.9、5236.8、10,418.1、10,721.3,结合maxDj比较可知备选地址3在权重距离增加值相对较小的情况下与最优解有较远的距离,因此应当将备选地址3作为二次选址的优先解。若备选地址3在地理环境上不适宜建址亦可考虑备选地址2。
同理,若选择备选地址3作为二次选址的解,以minU、maxDj与maxDjk作为目标函数,进行第三次选址,部分结果及其对应的多目标函数值如表4所示。

Table 4. Partial local optimal solutions of the third site selection
表4. 第三次选址的部分局部最优解
分析表4中数据可知,在6~10号备选点中,应当将备选地址6作为第三次选址的优先解。若备选地址6在地理环境上不适宜建址亦可考虑备选地址9。
综合以上计算结果与分析可得,S公司拟建的三所配送中心选址坐标为(1151696.7, 3456786.6)、(1147296.0, 3450386.0)、(1119693.4, 3419982.9)。转换为经纬坐标依次为(121.03˚E, 31.18˚N)、(120.30˚E, 31.69˚N)、(120.93˚E, 30.83˚N)。
通过卫星地图将三个拟建点坐标进行定位,从定位结果可看出,1号点位于江苏省昆山市淀山湖镇附近,此地交通便利,靠近苏沪高速及上海绕城高速,土地平整,适合建址;2号点位于江苏省无锡市惠山区附近,从卫星地图可看出此地临靠多条高速公路与省道,四通八达;3号点位于浙江省嘉兴市嘉善县附近,此地靠近G320,交通较为便利,适合建址。
6. 总结
本文在学习配送中心与选址问题的基本理论、模拟植物生长算法及其应用等研究的基础上,深入分析了S公司配送中心的选址问题,建立了相应的选址模型,并确立了影响S公司配送中心选址的相关因素以及计算各因素权重的方法,并在分析问题后利用改进后的模拟植物生长算法对所建模型进行求解。最后,带入目标服务城市的实际指标数据进行案例计算与分析,得出在区域内建立配送中心选址的理想坐标方位及布局。具体来讲,本文主要做了如下工作:
1) 本文在分析研究问题后引出了S公司配送中心选址的韦伯型多设施问题,并根据实际运用考虑,在选址模型中加入了配送中心之间的“排斥”作用,区别于传统的韦伯型连续选址模型。
2) 本文为求解构建的S公司配送中心选址模型,建立了相应的评价指标体系,且为了保证赋权的公正客观,使用了一种组合赋权法;并完成华东地区各目标坐标点的坐标转换,将选址问题与GIS学相结合。
3) 根据模拟植物生长算法存在的不足之处提出改进方案:利用有限元思想直接设定初始生长点与改变新枝生长角度,并通过算例验证了改进后算法的有效性。
NOTES
*第一作者。