1. 引言
锂原子参加的反应在早期宇宙的化学研究中非常重要。人们相信LiH分子的产生和消耗能为各种研究提供有用的参考 [1] [2] 。因此在过去的二十年里H + LiH及其同位素反应引起了人们的兴趣并被详细地研究。
最近,许多文献报道了关于LiH2和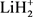 体系势能面的研究工作 [3] - [8] 。文献 [3] 利用自旋耦合价键理论计算了第一个关于LiH2体系的线型绝热势能面,研究发现了在线型路径上有一个小垒,其高度约为0.036 eV。Lee等人利用从头计算方法计算了H + LiH及其逆反应的基态势能面 [4],从初始态反应物到终态产物该势能面呈现了下坡下行的形状,文献同时指出了在反应过程中电子表面耦合的重要性。第一个三维解析势能面(DMJ势能面)是利用多体展开法拟合了从头算能量点 [5],文献同时计算了在不同碰撞能和选择的转动激发态下
体系势能面的研究工作 [3] - [8] 。文献 [3] 利用自旋耦合价键理论计算了第一个关于LiH2体系的线型绝热势能面,研究发现了在线型路径上有一个小垒,其高度约为0.036 eV。Lee等人利用从头计算方法计算了H + LiH及其逆反应的基态势能面 [4],从初始态反应物到终态产物该势能面呈现了下坡下行的形状,文献同时指出了在反应过程中电子表面耦合的重要性。第一个三维解析势能面(DMJ势能面)是利用多体展开法拟合了从头算能量点 [5],文献同时计算了在不同碰撞能和选择的转动激发态下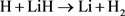 反应的积分反应截面。然而,他们发现在最小反应路径上不存在势垒。后来,Kim等人也利用高精度从头计算构建了该体系的势能面 [6],计算结果表明在共线路径(180˚)和垂直路径(90˚)上也不存在任何势垒。最近,Prudente等人利用精确从头算全组态相关方法改进了DMJ势能面并构建了一个新势能面(PMM势能面) [7] 。同年,Wernli等人也报道了一个LiH2体系的三维势能面 [8],研究同样指出在反应路径上不存在势垒。这一结论与文献 [5] [6] [7] 一致,但是与文献 [3] 结论相悖。
反应的积分反应截面。然而,他们发现在最小反应路径上不存在势垒。后来,Kim等人也利用高精度从头计算构建了该体系的势能面 [6],计算结果表明在共线路径(180˚)和垂直路径(90˚)上也不存在任何势垒。最近,Prudente等人利用精确从头算全组态相关方法改进了DMJ势能面并构建了一个新势能面(PMM势能面) [7] 。同年,Wernli等人也报道了一个LiH2体系的三维势能面 [8],研究同样指出在反应路径上不存在势垒。这一结论与文献 [5] [6] [7] 一致,但是与文献 [3] 结论相悖。
基于这些已有的势能面,人们开展了很多关于LiH2体系和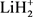 体系的动力学计算。Mahapatra [9] 等人利用含时波包方法(TDWP)计算了共线和三维结构下H + LiH (v = 0~3, j = 0~3)的反应几率,发现对于反应物无论处于何种状态,LiH分子的消耗反应通道几率低于H原子交换反应通道。后来,他们又利用DMJ势能面在0.9 eV范围内进行了含时波包计算,积分反应截面与文献 [5] 结果相差巨大。最近,刘玉芳 [10] 和Roy [11] 等人分别基于文献 [7] 势能面以及文献 [8] 势能面采用不同方法计算了H + LiH反应的动力学性质。从已有报道来看,利用最新势能面 [7] 计算的动力学工作还很少,考虑同位素效应的研究就更加稀少。另外,由于势能面的特征直接决定了反应过程的动力学特征,因此在不同势能面上的动力学结果还存在一些歧义 [5] [12] 。对于一个完整的化学反应过程,矢量的研究能提供更加丰富的动力学信息,只有标量与矢量的共同研究才能提供了一幅完整的动力学图像。基于以上考虑,本文利用准经典轨线方法在文献 [7] 提供的解析势能面上对H + LiH及其同位素反应D + LiD同步进行动力学计算,并且与已有数据进行比较。另外,我们还研究了反应物激发态对产物极化的影响。
体系的动力学计算。Mahapatra [9] 等人利用含时波包方法(TDWP)计算了共线和三维结构下H + LiH (v = 0~3, j = 0~3)的反应几率,发现对于反应物无论处于何种状态,LiH分子的消耗反应通道几率低于H原子交换反应通道。后来,他们又利用DMJ势能面在0.9 eV范围内进行了含时波包计算,积分反应截面与文献 [5] 结果相差巨大。最近,刘玉芳 [10] 和Roy [11] 等人分别基于文献 [7] 势能面以及文献 [8] 势能面采用不同方法计算了H + LiH反应的动力学性质。从已有报道来看,利用最新势能面 [7] 计算的动力学工作还很少,考虑同位素效应的研究就更加稀少。另外,由于势能面的特征直接决定了反应过程的动力学特征,因此在不同势能面上的动力学结果还存在一些歧义 [5] [12] 。对于一个完整的化学反应过程,矢量的研究能提供更加丰富的动力学信息,只有标量与矢量的共同研究才能提供了一幅完整的动力学图像。基于以上考虑,本文利用准经典轨线方法在文献 [7] 提供的解析势能面上对H + LiH及其同位素反应D + LiD同步进行动力学计算,并且与已有数据进行比较。另外,我们还研究了反应物激发态对产物极化的影响。
2. 计算方法
本文利用文献 [7] Prudente等人构建的PMM势能面进行计算,该三维势能面采用的解析函数基于多体展开方法,并且对处于电子基态的LiH2,LiH以及H2分子进行全组态相关计算。整体计算利用Gamess软件进行,选择了Dunning等人提出的aug-cc-pVQZ基组。文献同时指出在LiH消耗反应优先在共线结构下进行。DMJ势能面在反应物入口和产物出口处存在一个非物理的势阱,而在新的PMM势能面中则消失了,PMM势能面图形相比DMJ势能面更加平滑。尽管作者在该势能面上没有发现任何势垒,但是在随后刘玉芳等人利用该势能面进行准经典动力学计算时发现在共线构型下存在一个大约2.14 kcal/mole的小垒 [10] 。
在电子基态势能面上H + LiH的碰撞过程进行如下:
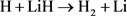 (损耗通道)
(损耗通道)
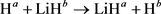 (交换通道)
(交换通道)
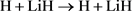 (不反应通道)
(不反应通道)
LiH分子损耗反应是一个高放热反应,在过程中大约放热为2.258 eV。从宇宙早期模型角度来看,LiH损耗反应更加重要,因此本文研究第一个通道反应即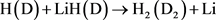 。本文采用的准经典轨线方法已经被广泛的应用到处理化学反应动力学过程。这里仅对与本工作相关的理论细节进行介绍。为描述矢量的方向,需要建立质心坐标系。在质心坐标系中,反应物的相对速度矢量k平行于z轴,y轴垂直于x-z平面,平面内包含了初始和最终相对速度矢量k和
。本文采用的准经典轨线方法已经被广泛的应用到处理化学反应动力学过程。这里仅对与本工作相关的理论细节进行介绍。为描述矢量的方向,需要建立质心坐标系。在质心坐标系中,反应物的相对速度矢量k平行于z轴,y轴垂直于x-z平面,平面内包含了初始和最终相对速度矢量k和 。反应物相对速度与产物相对速度方向的夹角用
。反应物相对速度与产物相对速度方向的夹角用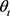 表示,
表示, 表示产物的转动角动量,
表示产物的转动角动量,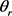 和
和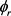 分别表示产物的角动量在质心坐标系下的二面角和方位角。通常,在质心坐标系中两矢量相关(
分别表示产物的角动量在质心坐标系下的二面角和方位角。通常,在质心坐标系中两矢量相关( ,
,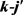 ,
,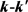 )可以展开为Legendre多项式的形式,相应于
)可以展开为Legendre多项式的形式,相应于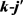 的
的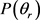 分布函数则可以写为
分布函数则可以写为

上式中的展开系数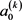 称为定向系数(奇数)或取向系数(偶数),可以用下式计算得到
称为定向系数(奇数)或取向系数(偶数),可以用下式计算得到
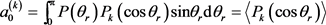
尖括号表示对所有轨线取平均。在计算中,当 展开到k = 18时,分布函数就得到收敛。
展开到k = 18时,分布函数就得到收敛。
全相关的角分布 可以用二面角分布函数
可以用二面角分布函数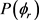 来描述,可以用傅里叶级数展开如下
来描述,可以用傅里叶级数展开如下
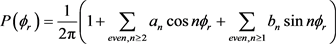
这里 ,
, 。在计算中,
。在计算中,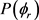 展开到n = 24,分布函数收敛结果比较理想。在计算过程中利用数值积分的方法求解哈密顿运动方程,积分采用四阶Runge-Kutta-Gill法和Hamming修正的四阶Adams-Moulton预测校正法。反应物分子轴的初始取向和振动初相位利用Monte Carlo理论随机取样。计算条件如下:碰撞能范围为0~2 eV。能量格点为0.1 eV,每个能量点计算2万条轨线。初始入射原子与靶分子之间的距离设置为10 Å,积分步长为0.1 fs,该时间数值足够小赖保证能量和角动量的收敛。在角动量J = 0和碰撞参数b = 0时,反应几率由P = NR/NT来确定,其中NR为反应的轨线数目,NT为计算的总轨线条数即2万。每条轨线的碰撞参数b通过b2在0到
展开到n = 24,分布函数收敛结果比较理想。在计算过程中利用数值积分的方法求解哈密顿运动方程,积分采用四阶Runge-Kutta-Gill法和Hamming修正的四阶Adams-Moulton预测校正法。反应物分子轴的初始取向和振动初相位利用Monte Carlo理论随机取样。计算条件如下:碰撞能范围为0~2 eV。能量格点为0.1 eV,每个能量点计算2万条轨线。初始入射原子与靶分子之间的距离设置为10 Å,积分步长为0.1 fs,该时间数值足够小赖保证能量和角动量的收敛。在角动量J = 0和碰撞参数b = 0时,反应几率由P = NR/NT来确定,其中NR为反应的轨线数目,NT为计算的总轨线条数即2万。每条轨线的碰撞参数b通过b2在0到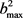 范围内随机选取得到。一旦计算得到反应几率,反应的积分反应截面就可以由下式给出
范围内随机选取得到。一旦计算得到反应几率,反应的积分反应截面就可以由下式给出 。
。
3. 结果与讨论
为了验证准经典轨线方法处理该反应体系的精确性,图1(a)和图1(b)分别计算了反应物处于基态的H + LiH and D + LiD反应几率。在该图中本文准经典计算结果和以前的量子计算以及准经典计算结果进行了比较。从图1(a)中可以看出,反应几率在低能区不存在能量阈值,而且随着能量的增加而逐渐降低,这一行为明显符合无垒放热反应的动力学性质。另外,由于Li原子相对较大的质量特征,从入射H原子到LiH分子的H原子端只形成一个窄小的接收锥,这也导致了LiH损耗反应几率的降低。量子结果在低能区存在一些共振峰,说明在低能区产生了短寿命的中间产物。共振峰结构随着能量的增加而逐渐消失,表明中间产物寿命逐渐减小,反应变得越来越直接。从图中可以看出文献 [10] 中Liu基于PMM势能面的结果是最小的,与本文计算结果和其它计算结果差异较大。相反地,本文的准经典结果和文献 [7] Prudente的量子含时波包计算的结果吻合的非常好。另外本文的计算结果与文献 [9] Padmanaban和文献 [11] Roy的计算结果基本上也符合,这说明本文利用准经典轨线理论处理H + LiH碰撞反应是可信的。图1(b)对比了文献 [10] 和本文利用同样的方法和同样的势能面对H + LiH同位素取代反应D + LiD的计算结果。从图上可以看出,计算结果趋势与H + LiH反应的结果趋势相似,但是在整个碰撞能范围内与文献 [10] 得到的数据表现出巨大的差异。对于基元反应而言,影响反应物分子靠近的主要因素是正比于碰撞能的离心势。碰撞能的增加导致离心势的增强,因此反应几率降低。从图中可以看出,两个同位素反应的反应几率也存在一些不同,在0.1到1.0 eV能量间,H + LiH的反应几率要低于D + LiD反应几率。
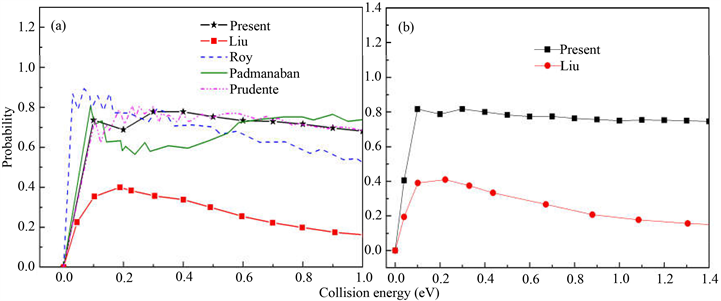
Figure 1. (a) Reaction probability for H + LiH; (b) Reaction probability for D + LiD
图1. (a) H + LiH反应几率曲线;(b) D + LiD反应几率曲线
图2(a)和图2(b)分别是H + LiH和D + LiD反应物分子处于基态时在0到1.0 eV碰撞能范围内的积分反应截面(ICS),从图上可以看出,我们的计算结果与除文献 [5] Dunne之外的其它计算结果是一致的。然而本文和文献 [10] Liu的准经典轨线结果比文献 [6] Kim文献 [11] Roy等人的量子结果要小一些。这部分可能是因为在准经典轨线理论中忽略了碰撞过程中的量子效应,其次由于文献 [6] [11] 与本文在计算时采取了不同的势能面导致的。由于在最小反应路径上不存在势垒,因此积分截面同样不存在能量阈值。积分反应截面随着碰撞能的增加而逐渐降低,这与反应几率的表现相似。在高能区,积分截面降低变慢,并且无论是量子结果还是准经典结果都趋向与同一数值。这种现象是因为在相对更高的碰撞能下,势能面开放更多的排斥区也进行了相互作用导致反应几率的降低。因此,碰撞能对反应几率或积分反应截面的影响是非常大的。
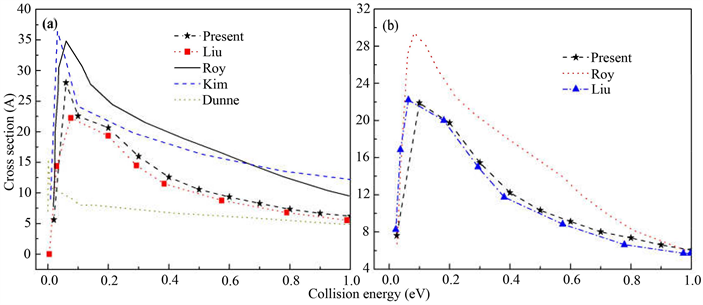
Figure 2. (a) Integral cross section for H + LiH; (b) Integral cross section for D + LiD
图2. (a) H + LiH积分反应截面曲线;(b) D + LiD积分反应截面曲线
随后再来讨论反应物初始振转激发态对两反应产物极化的影响。描述两矢量 和三矢量
和三矢量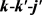 相关的
相关的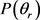 和
和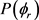 分布函数能提供产物转动角动量极化的丰富信息。在本文中,图3(a)和图3(b)分别计算了在1.2 eV碰撞能反应物分子LiH和LiD分别处于v = 1~3和j = 0状态下的
分布函数能提供产物转动角动量极化的丰富信息。在本文中,图3(a)和图3(b)分别计算了在1.2 eV碰撞能反应物分子LiH和LiD分别处于v = 1~3和j = 0状态下的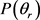 分布函数。从图上可以看出,无论在什么条件下,
分布函数。从图上可以看出,无论在什么条件下,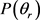 分布函数相对较宽,在
分布函数相对较宽,在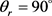 时存在一个极大的峰值,并且关于
时存在一个极大的峰值,并且关于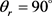 呈轴对称分布。这说明产物转动角动量矢量
呈轴对称分布。这说明产物转动角动量矢量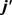 在垂直于反应物相对速度矢量
在垂直于反应物相对速度矢量 的方向上有强烈的取向分布。此外,随着反应物振动激发,即振动量子数从1增加至3,分布函数的峰值逐渐降低,说明产物转动角动量的取向程度逐渐变小。反应物分子的振动激发降低了角动量的各向异性分布。可以得出的是反应物分子LiH和LiD的振动激发对角动量
的方向上有强烈的取向分布。此外,随着反应物振动激发,即振动量子数从1增加至3,分布函数的峰值逐渐降低,说明产物转动角动量的取向程度逐渐变小。反应物分子的振动激发降低了角动量的各向异性分布。可以得出的是反应物分子LiH和LiD的振动激发对角动量 的取向产生了较大的影响。图4我们还研究了反应物初始转动激发对产物极化的影响。初始转动激发态选择为j = 3,5,7。从图中可以看出
的取向产生了较大的影响。图4我们还研究了反应物初始转动激发对产物极化的影响。初始转动激发态选择为j = 3,5,7。从图中可以看出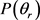 分布函数关于
分布函数关于 对称分布,其峰值随着转动量子数的增加而降低。转动激发对H + LiH的影响要比D + LiD略大。总之,反应物振动和转动激发对产物极化的影响是相似的。
对称分布,其峰值随着转动量子数的增加而降低。转动激发对H + LiH的影响要比D + LiD略大。总之,反应物振动和转动激发对产物极化的影响是相似的。
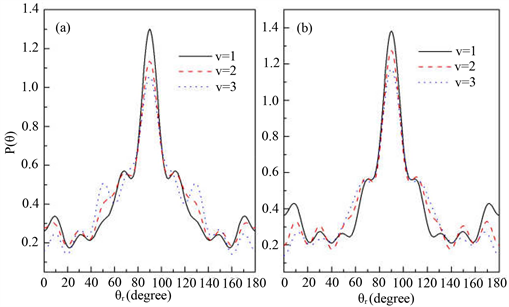
Figure 3.  distributions at the collision energy of 1.2 eV (a) for LiH (v = 1, 2, 3 j = 0); (b) for LiD (v = 1, 2, 3, j = 0)
distributions at the collision energy of 1.2 eV (a) for LiH (v = 1, 2, 3 j = 0); (b) for LiD (v = 1, 2, 3, j = 0)
图3. 能量为1.2 eV 分布函数(a)反应物状态LiH (v = 1, 2, 3, j = 0);(b) 反应物状态LiD (v = 1, 2, 3, j = 0)
分布函数(a)反应物状态LiH (v = 1, 2, 3, j = 0);(b) 反应物状态LiD (v = 1, 2, 3, j = 0)
图4(a)和图4(b)描述了在1.2 eV碰撞能以及反应物分子LiH和LiD处于v = 1,2,3和j = 0条件下的 分布函数。从图中发现描述
分布函数。从图中发现描述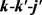 矢量相关的
矢量相关的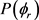 的分布并不关于
的分布并不关于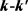 散射平面对称。从图4(a)来说对于每个振动激发而言并没有明显的单峰存在,但是很明显在
散射平面对称。从图4(a)来说对于每个振动激发而言并没有明显的单峰存在,但是很明显在 附近处的平均值要大于其它角度附近处的平均值。这说明产物H2转动角动量大体定向于y轴的正方向。不规则的趋势显示振动激发对H + LiH反应的
附近处的平均值要大于其它角度附近处的平均值。这说明产物H2转动角动量大体定向于y轴的正方向。不规则的趋势显示振动激发对H + LiH反应的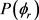 分布影响不大。图4(b)描述了D + LiD反应的
分布影响不大。图4(b)描述了D + LiD反应的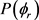 分布。与图4(a)不同的是在
分布。与图4(a)不同的是在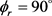 出现了3个峰值,但是分布依旧不是对称的。说明产物D2转动角动量强烈定向于y轴的正方向。随着振动量子数的增加,峰值稍有降低,说明反应的
出现了3个峰值,但是分布依旧不是对称的。说明产物D2转动角动量强烈定向于y轴的正方向。随着振动量子数的增加,峰值稍有降低,说明反应的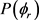 分布对反应物LiD的振动量子数比较敏感。为了获得更多有效的立体动力学信息,图5给出了转动激发对
分布对反应物LiD的振动量子数比较敏感。为了获得更多有效的立体动力学信息,图5给出了转动激发对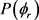 分布函数的影响。其中图5(a)表示H + LiH (v = 0, j = 3, 5, 7)反应的
分布函数的影响。其中图5(a)表示H + LiH (v = 0, j = 3, 5, 7)反应的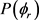 分布。在转动量子数j = 3时
分布。在转动量子数j = 3时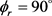 和
和 时均存在一个波峰,
时均存在一个波峰,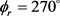 处的波峰要大于
处的波峰要大于 的波峰,说明产物转动角动量
的波峰,说明产物转动角动量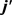 不但沿y轴取向,并且沿y轴负方向进行定向。但当j = 5和j = 7时,角动量的取向和定向都不明显。图5(b)的特征与图5(a)明显不同。在转动量子数取3时,只在
不但沿y轴取向,并且沿y轴负方向进行定向。但当j = 5和j = 7时,角动量的取向和定向都不明显。图5(b)的特征与图5(a)明显不同。在转动量子数取3时,只在 处出现一个波峰说明角动量强烈沿y轴取向。当反应物LiD被激发到j = 5时,角动量矢量不但发生取向还沿着y轴正方向定向。但是对更高的转动激发态j = 7,产物转动角动量均没有发现明显的取向或者定向。
处出现一个波峰说明角动量强烈沿y轴取向。当反应物LiD被激发到j = 5时,角动量矢量不但发生取向还沿着y轴正方向定向。但是对更高的转动激发态j = 7,产物转动角动量均没有发现明显的取向或者定向。
Figure 4. (a)  distributions for LiH (v = 1, 2, 3, j = 0); (b)
distributions for LiH (v = 1, 2, 3, j = 0); (b)  distributions for LiD (v = 1, 2, 3, j = 0) at the collision energy of 1.2 eV.
distributions for LiD (v = 1, 2, 3, j = 0) at the collision energy of 1.2 eV.
图4. 能量为1.2 eV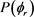 分布函数(a)反应物状态LiH (v = 1, 2, 3, j = 0);(b) 反应物状态LiD (v = 1, 2, 3, j = 0)
分布函数(a)反应物状态LiH (v = 1, 2, 3, j = 0);(b) 反应物状态LiD (v = 1, 2, 3, j = 0)
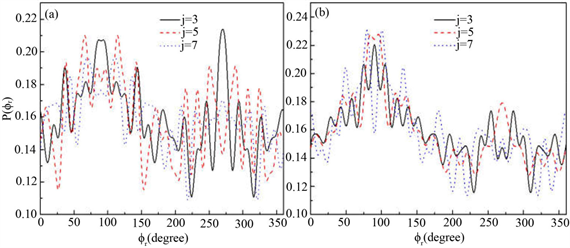
Figure 5. (a) 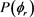 distributions for LiH (v = 0, j = 3, 5, 7); (b)
distributions for LiH (v = 0, j = 3, 5, 7); (b) 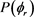 distributions for LiD (v = 0, j = 3, 5, 7) at the collision energy of 1.2 eV
distributions for LiD (v = 0, j = 3, 5, 7) at the collision energy of 1.2 eV
图5. 能量为1.2 eV 分布函数(a)反应物状态LiH (v = 0, j = 3, 5, 7);(b) 反应物状态LiD (v = 0, j = 3, 5, 7)
分布函数(a)反应物状态LiH (v = 0, j = 3, 5, 7);(b) 反应物状态LiD (v = 0, j = 3, 5, 7)
4. 结论
本文利用准经典轨线理论在Prudente等人构建的从头算势能面上研究了H + LiH及其同位素取代反应D + LiD的立体动力学性质。计算的反应几率及积分反应截面与已有的大部分理论计算数据非常吻合,与刘玉芳等人和Dunne等人的计算结果有所不同。该反应的动力学变化符合一般情况下无垒放热反应过程所表现出来的行为。由于Li原子的质量较大,导致接收锥较小,从而抑制了反应的进行。另外反应物分子沿着垂直于相对速度矢量k的方向取向,且取向程度随振转量子数的增加而降低。如文中所述,激发态对产物转动角动量 有着复杂的影响。本文的工作同时也验证了PMM势能面的精确性,不仅适合进行准经典动力学计算还适合更为精确的量子波包计算,尤其是态–态动力学计算。
有着复杂的影响。本文的工作同时也验证了PMM势能面的精确性,不仅适合进行准经典动力学计算还适合更为精确的量子波包计算,尤其是态–态动力学计算。