1. 引言
无论是在控制理论还是工程领域,最优化控制问题都是一个重难点。最优控制问题的求解依赖于求解HJB方程,由于系统一般是非线性的,导致对于求解HJB方程很困难,难以得到解析解 [1] 。
Bellman在1957年首次提出了动态规划方法。动态规划对于求解最优控制问题是一个行之有效的方法。该方法适应广泛:离散系统,连续系统,非线性系统,以及随机系统等等。但是该方法是一种逆向计算方法,随着解的时间维度增加,且由于控制变量维数大容易造成“维数灾难”问题。于是近年来,针对未知的复杂非线性系统的最优控制问题,自适应动态规划应运而生。与传统的动态规划相比,由于其采用函数近似结构来逼近系统模型,评价指标 [2] ,和控制策略,避免了因时间逆向计算造成的“维数灾难”问题。自适应动态规划可用于大规模非线性系统 [3] ,其应用也相当广泛;例如:机器人运动规划 [4] ,无人驾驶汽车 [5] ,污水处理系统 [6] 等等。
LIU等采用值迭代的自适应动态规划,并证明其收敛条件是迭代性能指标函数初始化为任意半正定函数 [7] 。根据此收敛条件,提出了一种基于自适应动态规划的协同优化算法 [8] 。该协同优化算法令迭代的残差快速减小,大幅提高了自适应动态规划的收敛速度。LIU等对于离散的非线性系统采用基于策略迭代的自适应动态规划方法 [9] ,证明了该迭代控制律可以使系统稳定,并说明其是收敛的。LUO等则分别对于连续时间非线性系统采用基于策略迭代的自适应动态规划方法 [10] ,该策略迭代的实现使用基于神经网络的最小二乘方法并证明该方法是收敛的。文献 [11] 针对离散时间非线性系统,提出了策略梯度自适应动态规划算法,并证明了该算法中Q函数能收敛到最优值。
由于神经网络良好的自适应与自学习等特点 [12] ,本文采用神经网络与动态规划结合的自适应动态规划对无模型的最优控制问题进行求解。对于神经网络的权重系数采用离线数据集与在线数据结合进行更新。
2. 问题描述
本文所描述的离散时间非线性系统为:
(1)
其中
为状态向量,
为控制向量。此外X和U为一个完备集合,
。系统(1)在X上稳定,函数
在集合D上连续,且
,
是系统(1)的一个稳定状态。本文考虑的是无模型的最优控制问题,即函数
的具体解析式是不知道的。优化目标是找到一个稳定的反馈控制
,使得性能指标函数(2)最小。
(2)
其中
, 和
为正定函数。
和
为正定函数。
3. 策略梯度自适应动态规划
对于上述最优控制问题,由于该系统是非线性的且系统模型
的解析式并不知道。为了克服这些困难,引入了策略梯度自适应动态规划来求解该最优控制问题。
定义1对于系统(1),如果
在X上连续,且
,
,则称控制
是可控的,记
。基于自适应动态规划理论,定义值函数
为:
(3)
易知:
(4)
记最优值函数为:
(5)
对应的最优控制为:
(6)
根据自适应动态规划,为了更好求解该最优控制问题,下面引入Q函数:
(7)
且易知
,Q函数也可以表示为:
(8)
对应最优控制
的最优Q函数为:
(9)
相应的最优控制 为:
为:
(10)
为了求解该最优控制问题,通过迭代的思想,希望利用Q函数的梯度信息来更新控制策略u,然后把控制策略u带入Q函数。策略梯度自适应动态规划算法的具体步骤如下:
步骤1:给定初始控制策略
和允许误差
,且令
。
步骤2:估计Q函数:
(11)
步骤3:更新控制策略u:
(12)
其中
为常数。
步骤4:若
,则输出Q函数和控制策略,否则令
,返回步骤2。
对于系统(1),首先定义其Hamiltonian函数为:
(13)
且
。
引理1 [11] 给定
,根据策略梯度自适应动态规划算法得到控制序列
。假设
,
,
和
存在,且
,
,
。
,
。如果对于
,
且
,则:
1) ,
,
2)
。
证明:1) 将Hamiltonian函数
在
处进行二阶泰勒展开:
(14)
根据式(8)和(13)易知:
(15)
(16)
由于
,对于
都存在,因此
都存在。由式(12)和(14)~(16)易知:
令
,且
,则:
(17)
如果
,当
时,其中
,
,则:
(18)
即
。根据Hamiltonian函数定义知:
。
故:
。
2) 假设
,对于系统
,则对于Lyapunov函数
有:
(19)
由
,知:
。即:
。
对于所有
,根据定义1知:
。由数学归纳法知,当
,有
。
引理2 [11] 对于所有
,根据策略梯度自适应动态规划算法得到序列
和
满足:1)
,
2)
。
证明 1)由式(4)和(8)知:
(20)
且:
(21)
则对于所有
,有:
(22)
由于式(9)知:
(23)
故可得:
。
2) 由式(12)知,当i趋于
时有:
(24)
即:
(25)
由式(8)知:
(26)
则有:
(27)
又由式(4)知:
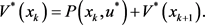 (28)
(28)
上式对u求导得:
(29)
易知式(27)和(29)是一样的,由唯一性得:
(30)
由式(26)得:
(31)
由结论1)知,序列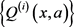 是单减序列,记
,则有:
是单减序列,记
,则有:
。
4. 基于数据驱动的神经动态规划及其实现
首先定义一个数据
其中
为当前状态x执行控制动作a后得到状态向量。
的获得是通过实际系统输入控制动作a后得到,而不是使用系统模型f的数学解析式。如图1,是策略梯度自适应动态规划算法的结构。其中包括两个部分:离线数据集和在线数据。离线数据集 。M为数据的数量,其中离线数据集
可以通过实际系统随机采样获得,其结构如图2。在线数据
,其分别是在时刻
和k的在线状态和控制信息,其获得的结构图如图3。图1的大概流程是:首先,给定一个初始控制
,根据离线数据集
通过策略梯度自适应动态规划算法步骤2,得到
。其次,将初始控制
通过实际系统作用于当前状态
,得到下一状态
,即得到在线数据
。然后,将
和
通过策略梯度自适应动态规划算法步骤3,得到
。最后,将
加入离线数据集
作为新的离线数据集,以此重复循环,则可得到在线数据
,控制序列
和Q函数序列
。
。M为数据的数量,其中离线数据集
可以通过实际系统随机采样获得,其结构如图2。在线数据
,其分别是在时刻
和k的在线状态和控制信息,其获得的结构图如图3。图1的大概流程是:首先,给定一个初始控制
,根据离线数据集
通过策略梯度自适应动态规划算法步骤2,得到
。其次,将初始控制
通过实际系统作用于当前状态
,得到下一状态
,即得到在线数据
。然后,将
和
通过策略梯度自适应动态规划算法步骤3,得到
。最后,将
加入离线数据集
作为新的离线数据集,以此重复循环,则可得到在线数据
,控制序列
和Q函数序列
。

Figure 1. Policy gradient adaptive dynamic programming algorithm
图1. 策略梯度自适应动态规划算法
4.1. 神经动态规划的实现设计
由于根据策略梯度自适应动态规划算法,要求去计算未知的Q函数
和控制策略
,为了实现该过程,下面引入执行―评价神经网络。其中用执行网络来逼近控制策略
,用评价网络来逼近Q函数
。首先介绍俩组线性无关的基函数:
,
。其中
。根据代数理论,控制策略
和Q函数
可以如下线性表示:
(32)
(33)
根据函数逼近理论,Q函数
和控制策略
可以被有限维基函数近似表示:
(34)
(35)
其中
和
分别为执行网络和评价网络的权重系数向量,但其是未知的。
和
分别为执行网络和评价网络的激活函数向量。则该神经网络的输出可以表示为:
(36)
(37)
其中
和
分别为
和
的近似估计。由于神经网络有误差,在用
和
估计
和
时会产生残差,定义Q函数残差为:
(38)
下面的目标是,在满足残差趋于0的条件下,基于数据驱动来计算
,
。任意
和
,定义内积
。令:
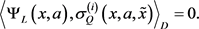 (39)
(39)
将(38)式带入(39)式得:
(40)
则可得:
 (41)
(41)
在计算
时,其中涉及许多积分,根据蒙特卡洛积分方法,令:
。首先基于离线数据集
来计算
:
(42)
其中
。同理可得:
(43)
(44)
且
,
。则可得:
(45)
如图4,基于离线数据集
可以计算出
,当
时,对于在线数据
,此时把在线数据
加入到离线数据集
作为新的离线数据集
,且用其来计算
:
(46)
(47)
(48)

Figure 4. Neural dynamic programming algorithm
图4. 神经动态规划算法
其中
,
则由(41)式知,当
时:
(49)
接着需要计算执行网络的权重系数
,由神经动态规划算法步骤3更新控制策略时,用
替换
会产生误差,定义控制策略残差为:
(50)
同理在计算
时要满足控制策略残差趋于0:
(51)
即:
(52)
则可得:
(53)
根据蒙特卡洛积分方法,令:
。基于离线数据集
,当
时,对于在线数据
,此时把在线数据
与离线数据集
结合,且用其来计算
:
(54)
(55)
其中
,且
,
。则由(53)可得:
(56)
4.2. 神经动态规划算法
步骤1:收集离线数据集
,计算
。
步骤2:给定一个初始允许误差
和初始控制策略
,并令
。
步骤3: 使用
和
计算
。 并根据(49)式计算
。
步骤4:使用离线数据集
和在线状态数据
,计算
,并根据(56)式计算
。
步骤5:若
,则输出
和
;否则令
,返回步骤3,继续循环。
5. 结束语
本文提出了一种基于数据驱动的神经动态规划方法。该方法不依赖于系统的数学解析式,采用神经网络与动态规划结合的方式对最优控制问题进行求解。其分别利用Q函数的残差和Q函数的基函数做内积为零,控制策略的残差与控制策略的基函数做内积为零;并使用离线数据集与在线数据来迭代更新神经网络的系数,最后得到所需的控制策略。该方法能将离线数据与在线数据有效结合,使得系数更新更加完善。并且证明该算法是收敛的;且收敛到最优值。
基金项目
广东省自然科学基金项目(No.2018A030313505),广东省科技计划项目(No.2017B010124003, No.2017 B090909001)。