1. 引言
Km,n表示完全二部图,其两个部分点集X和Y分别具有m和n个点。lKm,n表示完全二部多重图,它是l个两两不交的同构于Km,n的图的并。如果lKm,n的一个子图F包含了lKm,n的所有点,则称F为lKm,n的一个支撑子图。若lKm,n的支撑子图F的每个分支均同构于图Kp,q,则称F为lKm,n的一个Kp,q-因子。如果lKm,n的边集可以划分为lKm,n的Kp,q-因子,则称lKm,n存在Kp,q-因子分解。在综述文章 [1] 中,Ushio称lKm,n的Kp,q-因子分解为可分解的(m, n, k, l)二部Kp,q-设计。如果lKm,n存在Kp,q-因子分解,则称lKm,n是可Kp,q-因子分解的。本文用到的图论方面的名词术语,均参照图论著作 [2] 。
lKm,n的Kp,q-因子分解有许多应用,特别是Yamamoto和Ushio等 [3] 用其建立了计算机数据存储的HUBMFS2方案。当p = 1和q = 2时,Ushio [4] 、Wang和Du [5] 完全解决了lKm,n的K1,2-因子分解的存在性问题。Martin在论文 [6] [7] 中分别解决了当p = 1、q = 3与p = 1、q = 4时Km,n的Kp,q-因子分解的存在性。当p = 2和q = 3时,Wang和Du [8] 完全解决了l = 1时Km,n的K2,3-因子分解的存在性。我们在论文 [9] 中完全解决了l > 1时lKm,n的K2,3-因子分解的存在性。本文研究当p = 2和q = 4时,完全二部多重图lKm,n的K2,4-因子分解的存在性。即我们将证明lKm,n存在K2,4-因子分解的充分必要条件。
定理1.1:完全二部多重图lKm,n存在K2,4-因子分解的充分必要条件是:1)
(mod 2),2) m £ 2n,3) n £ 2m,4)
(mod 6),5)
是整数。
2. 定理1.1的证明
定理1.1的必要性证明通过简单计算即可得到,充分性部分的证明由以下几个引理构成,第一个引理是显然的,其中
表示x和y的最大公约数。
引理2.1:设u,v,x和y是正整数。如果
,则
。
引理2.2:设s是任意正整数。如果lKm,n存在K2,4-因子分解,则lsKm,n存在K2,4-因子分解。
证明:重复lKm,n的K2,4-因子分解s次即得lsKm,n的K2,4-因子分解。
引理2.3:设s是任意正整数。如果lKm,n存在K2,4-因子分解,则lKms,ns存在K2,4-因子分解。
证明:由于Ks,s是可1-因子分解的(参见 [2] ),可设
是它的一个1-因子分解。对于每一个1 £ i £ s,用lKm,n代替Fi的每条边,即得到lKms,ns的一个支撑子图Gi,且
边集的并为lKms,ns。由于lKm,n是可K2,4-因子分解的,因而Gi也是可K2,4-因子分解的。所以lKms,ns存在K2,4-因子分解。
由引理2.3我们易得当m = 2n或n = 2m时,lKm,n存在K2,4-因子分解。因此下面我们只需考虑m < 2n且n < 2m时的情形。在这种情形下,我们令
,
,
和
。由定理1.1的条件(1)~(4)可知a,b,t,r是整数,且0 < a < m,0 < b < n。于是有2a + 4b = m,4a + 2b = n。进而可得
。设
,它也是整数。设
,2a = dp,4b = dq,其中
。因此
。于是我们可得下列各式:
则有以下引理
引理2.4:1) 如果
,
,设
,则
,
其中s是正整数。
2) 如果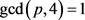 ,
,设
,设
,则
,
,设
,设
,则
,
其中s是正整数。
3) 如果
,
,设
,设
,则
,
其中s是正整数。
4) 如果
,
,设
,设
,则
,
其中s是正整数。
5) 如果
,
,设
,设
,则
,
其中s是正整数。
6) 如果
,
,设
,设
,则
,
其中s是正整数。
7) 如果
,
,设
,设
,则
,
其中s是正整数。
证明:1) 由条件我们有
,因此
。此时
。根据引理2.1,我们有
。所以
是正整数。令
。设
,
。由
,
。我们知
和
是正整数。因为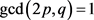 ,所以
是正整数,这里
。令
,即得(1)中的等式。
,所以
是正整数,这里
。令
,即得(1)中的等式。
(2)~(7)中各式的证明类似于(1)。
引理2.5:对于任意正整数γ,p和q,如果
,
,则当
是正整数时,γKm,n存在K2,4-因子分解。
证明:记
,
,
,
和
。并令X和Y是γKm,n两个部分点集
,
。
我们将构作γKm,n的一个K2,4-因子分解。我们约定xi,j和yi,j的第一个下标分别在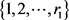 和
中进行模r1和模r2的运算,它们的第二个下标分别在
和 {
中进行模
和模
和
中进行模r1和模r2的运算,它们的第二个下标分别在
和 {
中进行模
和模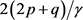 的运算。
的运算。
对于每一个正整数i,x,y,z,1 £ I £ p,0 £ x £ 1和0 £ y £ 3,令
,
,
并构作如下边集
。
对于每一个正整数i,x,y,z,1 £ i £ q和0 £ x,y,z £ 1,令
,
并构作如下边集
。
令
,则图F就是γKm,n的一个K2,4-因子。定义
到
上的双射
,
。对于每一个
和每一个
,令
。
易证每一个图
都是γKm,n的K2,4-因子。于它们边集的并构成γKm,n,因此
就是γKm,n的一个K2,4-因子分解。
引理得证。
以下引理的证明同引理2.5相类似,因此我们只写出其中X,Y,Ei和
的表达式。
引理2.6:对于任意正整数γ,p和q,如果
,
,则当
是正整数时,γKm,n存在K2,4-因子分解。
证明:记
,
,
,
和
。并令
,
。
对于每一个正整数i,x,y,z,1 £ i £ p,0 £ x,y,z £ 1,令
,
,
并构作如下边集
。
对于每一个正整数i,x,y,z,1 £ i £ q,0 £ x,y,z £ 1,令
,
,
并构作如下边集
。
引理2.7:对于任意正整数γ,p和q,如果
,
。则当
是正整数时,γKm,n存在K2,4-因子分解。
证明:记
,
,
,
和
。并令
,
。
对于每一个正整数i,x,y,1 £ i £ p,0 £ x £ 1和0 £ y £ 3,令
,
,并构作如下边集
。
对于每一个正整数i,x,y,z,w,1 £ i £ q,0 £ y,w £ 1和0 £ x,z £ 3,令
,
并构作如下边集
。
引理2.8:对于任意正整数γ,p和q,如果
,
。则当
是正整数时,γKm,n存在K2,4-因子分解。
证明:记
,
,
,
和
。并令
,
。
对于每一个正整数i,x,y,满足1 £ i £ p,0 £ x £ 1和0 £ y £ 3,令
,
,并构作如下边集
。
对于每一个正整数i,x,y,z,s,t,且1 £ i £ q,0 £ x £ 3,0 £ y,z,s,t £ 1,令
,
,
并构作如下边集
。
定理1.1的证明:定理1.1必要性的证明显然。结合引理2.2和引理2.8,即可完成定理1.1充分性的证明。
基金项目
国家自然科学基金资助项目(11571251)。