1. 引言
随着控制工程、机电一体化、人工智能等多个领域的高速发展,物流系统开始向自动化、无人化、智能化发展,RGV (Rail Guide Vehicle)有轨制导车辆系统也随之出现。RGV是一种无人驾驶、在轨道自由运行的智能车,能根据指令自动控制移动方向和距离。它既可作为立体仓库的辅助设备,也有自己独立运行的系统,被广泛应用于现代化物流体系。因此,如何通过合理的调度规则提高RGV的工作效率是急需解决的问题。
本文研究智能加工系统(见图1)的RGV的最佳动态调度策略 [1] ,该系统由8台计算机数控机床(Computer Number Controller,CNC)、1辆RGV、1条RGV的直线轨道、1条上料传送带、1条下料传送带等设备组成。在设备正常工作时,若有CNC处于空闲状态,则会立即向RGV发出上料需求信号;否则,CNC处于加工状态。当RGV在接到上料需求信号时,RGV需确定最佳的上下料及移动策略。RGV在下料完毕后,需先对熟料进行清洗才能将熟料放置下料传送带,并且在清洗熟料时,RGV不能移动。

Figure 1. Schematic diagram of RGV working principle
图1. RGV工作原理示意图
2. 模型假设与符号说明(表1)
我们做以下假设:
1) 假设上下料传送带都是连续不断的,能及时为RGV提供生料和运输熟料;
2) 假设RGV在完成上下料作业后即刻进入清洗作业阶段;
3) 假设每班次连续工作八小时;
4) 作业开始时,RGV的初始位置位于1号CNC前;
5) 假设该班次结束时仍处于加工状态的物料不计入生产件数。
3. RGV动态调度问题的数学模型
我们以系统工作时间最少为目标建立模型。显然,单位作业时间的长短是由CNC加工时间和RGV移动作业时间共同决定的。因此,我们考虑利用CNC加工、RGV移动、清洗等工作,制定相应的动态调度模型,以尽量减少系统的空闲时间为目标进行调度。我们将距离时间化,以RGV可移动到的四个位置和八个CNC的位置作为节点,以相应过程的时间作为权值,建立基于有向图的优化调度模型。这样时间最短问题转换为图论问题中的最短路径问题。注意到,我们的目标应是使物料尽快进入工作状态,而不是使物料尽快移动到指定地点。例如,时刻t时RGV的初始位置在A处,若
= 10 s,
= 8 s,
= 0 s,则RGV不移动,等待1号CNC加工完毕后进行上下料更为。因此,当RGV进入空闲状态时,为了使每步调度都达到当前最优,我们为每个CNC引入一个虚拟节点,权值为
,则当RGV进入空闲状态时,可令RGV进行一次搜索,找出距离RGV当前位置最近的虚拟节点,其对应的CNC即为RGV下一步作业的目标。
3.1. 节点说明
节点集合V包含三种节点:RGV可移动到的位置节点,每台CNC所处位置的节点、虚拟节点(见图1)。用
表示RGV位置节点,
表示8台CNC位置节点,
表示虚拟节点位置。
3.2. 权值说明
用
表示从
到
的一条边,
为对应权值,同时也表示相应的工作时间或移动时间,其中
, 表示任一节点。图的边集E包含以下三个部分:
1) RGV位置节点
之间的权值。
2) RGV位置节点(用
表示)与CNC位置节点(用j表示)间的权值。弧
表示RGV为CNC上下料,权值为上下料所需时间。弧
表示RGV清洗熟料,当CNC未加工处于空闲时,无熟料产生,下料为空,不进行清洗操作,权值为0 s;当CNC已加工完处于空闲时,有熟料产生,进入清洗作业阶段,权值为清洗作业所需时间
,如公式(1)所示。
(1)
3) 环
表示RGV不进行任何操作,权值为等待时间。因此,图
的点集和边集 [2] 可表示为:
(2)
由图2所示,结合图论的Floyd算法,我们以减少系统空闲时间为目标设立调度规则,求出一个班次内加工物料的编号、上下料时间、CNC编号以及最大加工物料数,从而给出调度策略。
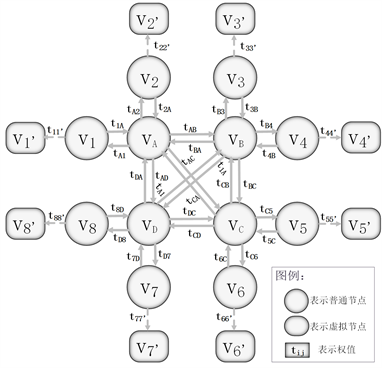
Figure 2. Scheduling optimization of network diagram
图2. 优化调度图
RGV作业周期 [3] :当工作状态达到稳定后,RGV访问CNC的次序不再改变,将此时依次访问各CNC编号序列的最小重复单元个数
定义为周期长度,则RGV 连续访问
个CNC可定义为一个作业周期。
RGV作业序列:将一个周期内RGV依次访问各CNC的编号顺序定义为作业序列,并表示为:
(3)
当RGV在一个作业周期内消耗时间达到最少时,为最优作业序列,记作
。
4. 基于图论的RGV动态调度算法
对于RGV动态调度问题,两道工序与多道工序没有本质的区别。因此,我们仅考虑一道工序和两道工序两种情形。在一道工序物料加工作业时,每台CNC配置相同的刀具,物料可在任一台CNC上进行加工;在两道工序物料加工作业时,每个物料需在不同CNC上依次完成两道工序。我们先给出一道工序物料加工时RGV的动态调度算法,在此基础上给出两道工序物料加工时RGV的动态调度算法。
4.1. 一道工序物料加工作业——算法一:基于贪心算法的RGV动态调度算法
结合贪心算法在图论中的应用 [4] ,我们为该调度模型制定了一个规则,通过Floyd算法求得任意点到某虚拟节点最短距离,提出基于贪心算法的规则求解算法,最终得到一个较好的局部最优解,如图3。

Figure 3. Solution flow based on Greedy Algorithm
图3. 基于贪心算法的求解算法
用
表示CNC工作状态:
(4)
用
表示RGV清洁槽内是否有熟料:
(5)
步骤一:用t表示当前作业时间,
表示t时刻RGV所处位置,t的初值为0,此时RGV处在A位置。
步骤二:使用Floyd算法寻找距RGV当前位置最近的虚拟节点,则该虚拟节点所对应的CNC即为RGV下一步的目标CNC。
步骤三:RGV移动到权值最小的CNC后,RGV开始等待,判断CNC的工作状态并确定等待时间。
1) 当
= 0时,CNC处于空闲状态,等待0 s,RGV进行上下料,但下料为空并记录上料时间和CNC编号;
2) 当
= 1时,CNC已加工完毕,等待0 s,RGV进行上下料,记录上下料时间和物料序号
;
3) 当
= 2时,CNC正在加工,等待剩余加工时间为
。
步骤四:判断RGV清洁槽内有无熟料,当
= 1时,进行清洗作业并判断总作业时间t是否超过超过一个班次的作业时间;当
= 0时,直接判断作业时间t是否超过一个班次的作业时间,若未超过,返回步骤二;若超过,结束循环,并输出一个班次内的物料编号、上下料时间以及最大加工物料数。
4.2. 两道工序物料加工作业——算法二:改进型模拟退火算法
4.2.1. 算法一的改进
由于CNC分为两种加工方式,因此在算法一中需增加一步判断:
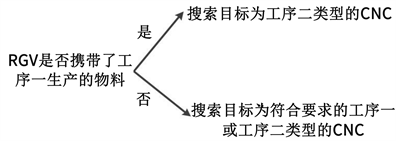
4.2.2. 改进模拟退火算法
问题分析中已指出,模拟退火(SA)算法 [5] 具有局部搜索能力强,运行时间较短的优点,但其全局搜索能力较差,极易受到参数影响。因此我们使用粒子群(PSO)算法对其进行改进,使其参数可以进行动态调整从而克服算法的局限性。针对当前问题,我们借助改进后的算法一求得一个班次内的生产件数,然后通过改进的模拟退火算法搜索生产件数最大值,其对应的工序分配即为最优分配。算法流程见图4。
1) 算法二迭代过程
a) 生成m个粒子作为初始种群,赋给粒子的位置初值,给定初始接受概率p、初始温度T、终止温度
、温度动态衰减系数
、迭代次数
。
b) 判断算法是否达到循环终止条件:
i) 循环次数
从1循环至
;ii) 体系降温至终止温度的
。
c) 计算每个粒子适应度
、
i) 若粒子的适应度优于原个体极值
,则进行更新并选择最优个体值作为群体极值
。
ii) 若粒子的适应度不能优于原个体极值
,则更新
,并以
为概率接受当前适应度作为
;若未接受粒子的新适应度,则不做更新。

Figure 4. Improved simulated annealing algorithm
图4. 改进的模拟退火算法
d) 在每个粒子当前位置中增加一个服从正态分布的随机值作为新的粒子位置。
e) 根据粒子个体适应度和平均适应度,计算温度自动衰减系数k。
f) 更新当前环境温度:
。
迭代完成后得到
为函数的最优值。
2) 退火速度的改进
模拟退火算法的全局搜索能力取决于退火速度。一般固定温度衰变无法感知当前的收敛情况,因此我们引入温度动态衰减系数,使得算法可以根据当前粒子已知种群的适应度来感知局部和全局收敛情况,保证搜索过程不至于过早收敛陷入局部最优解。温度动态衰减系数为:
(6)
其中,
为种群的平均适应度,
为当前粒子的适应度,
为初始温度衰减系数,
表示标准正态分布,
为上一次迭代中的粒子温度。
3) 最优分配的计算
a) 生成服从均匀分布
的随机数并取整数后得到粒子初始位置,并转为八位二进制编码(不足八位在数字最前补零)。加工第一道工序的CNC用“1”表示,加工第二道工序的CNC用“0”表示,第 位数字表示编号为
的CNC。
b) 将得到的二进制八位数代入基于贪心算法的求解算法中得到当前粒子位置对应的适应度
,即八小时的生产件数。
c) 带入算法中迭代求得函数最优值
,并将其对应的粒子位置转化为八位二进制数字,即得机器工序的最优分配。
5. 仿真结果分析
假设我们所研究的RGV智能加工流水线的五组参数如表2所示,单位为秒。将表2中的五组系统作业参数分别代入算法一,得出一道工序物料加工作业的产量和最优作业序列,具体结果见表3。
针对两道工序物料,将表2中的五组系统作业参数分别代入算法二,可得出两道工序物料加工作业的产量、最优作业序列和最佳工序分配,具体结果见表4。

Table 2. System operating parameters
表2. 系统作业参数

Table 3. Production situation of material processing in single procedure
表3. 一道工序物料加工作业的生产情况

Table 4. Production situation of material processing in double procedure
表4. 两道工序物料加工作业的生产情况
6. 结论
本文基于图论,给出了RGV作业时的动态调度策略,并通过实验发现RGV作业时访问各CNC的次序会逐渐稳定,从而得出RGV的最优作业序列。虽然我们所建的RGV智能调度模型基于贪心算法的思想,但通过对一道工序物料加工作业结果的分析,可验证出在本问题的背景下,我们所求出的局部最优解即为全局最优解。