1. 引言
积雪是冰冻圈的主要存在形式之一,一方面是全球气候变化系统的重要组成部分,另一方面又在全球水能循环中扮演着极其关键的角色,对水资源和环境有着不可忽视的影响。积雪通过直接反射减少下垫面接收到的太阳短波辐射并且阻碍下垫面与大气之间的热量交换,同时,积雪的融化还将引起水文条件的变化 [1] 。积雪深度是表征积雪特征的重要参数,我国积雪深度有3个主要的高值区:一是东北地区,二是新疆北部,三是位于喜马拉雅山脉北麓以西藏地区南部为代表的高原南部高值区 [2] 。积雪对气候的反馈作用有两种,一种是通过积雪表面的高反照率影响地表能量平衡;另外一种是通过改变土壤湿度来影响地表温度的回升,进而对气候产生影响,它不仅是最活跃的环境影响因子,也是最敏感的环境变化响应因素 [3] [4] 。在西藏的一些地区,由于雪量过大、积雪过深、持续时间过长、积雪的长时间不化,对牧业生产和牧民的生活会产生负面影响 [5] ,分析与研究积雪深度的变化情况对农业生产和牧业生产都具有十分重要的意义。巴桑等 [6] 利用1980~2009年气象台站的地面观测数据、卫星资料从不同角度对近30 a来西藏区域积雪变化趋势进行了分析,结果表明:不同资料分析均显示,近30 a来西藏地区积雪变化趋势都与各季节的气温和降水密切相关。韦志刚等 [7] 选取了青海省和西藏自治区境内的72个气象站逐日观测的积雪深度资料,分析了青藏高原积雪的空间分布和年代际变化特征,结果表明:高原积雪的年变化并不完全一致;青藏高原的积雪主要发生在10月至5月份,9月和6月的积雪相对来说很少,7月和8月基本无积雪,即夏季基本无明显积雪,青藏高原积雪总的来说呈平缓的增长态势。白淑英等 [8] 利用1979~2010年逐日中国雪深长时间序列数据集,采用GIS空间分析和地统计方法,分析了青藏高原积雪深度的时空变化规律及异常空间分布特征,结果表明:近32年来,青藏高原雪深呈显著增加趋势,尤以冬季增加最为明显。王叶堂 [9] 等利用MODIS卫星反演的积雪资料以及同期气象资料,分析了2000~2005年青藏高原积雪分布特征、年际变化及其与同期气温和降水的关系,结果表明:青藏高原积雪分布极不均匀,四周山区多雪,腹地少雪;高原积雪期主要集中在10月到翌年5月;气温和降水是影响高原积雪变化的基本因子;冬季,高原积雪面积变化对降水更为敏感;春季和秋季,气温是影响高原积雪面积变化更主要的因素。
青藏高原积雪变化对全球气候变化的诊断分析具有重要意义,雪量过大,积雪过深,持续时间过长,积雪的长时间不化,对牧业生产产生负面影响,因此,分析与研究西藏地区积雪深度对未来西藏雪灾预测具有指导意义。
2. 资料与方法
2.1. 数据介绍
本文所用原始资料来自西藏地区39个气象观测站1979至2013三十五年的地面逐日观测资料(图1),包括逐日降水量(mm)、平均气温(℃)、最低气温(℃)、最高气温(℃)和积雪深度(cm)。由于高原积雪期主要集中在每年秋季至翌年春季,即夏季无明显积雪,所以本文只取西藏地区春、秋、冬三季的数据进行分析。
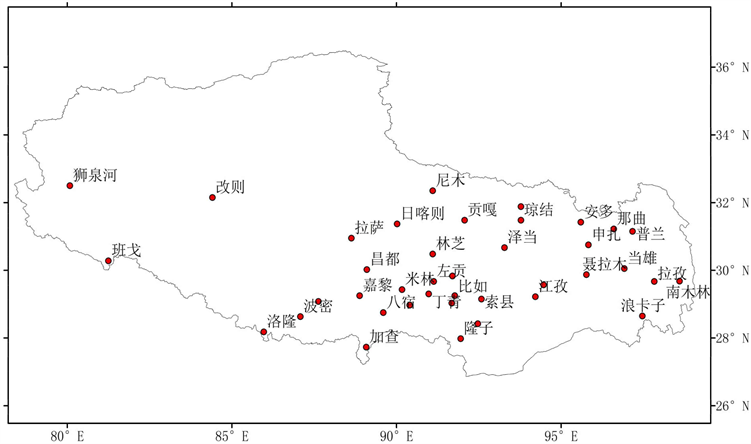
Figure 1. Distribution of stations in the study area
图1. 研究区站点分布
本研究在建立积雪深度多元回归拟合模型之前,首先对数据进行了处理:① 剔除各个台站缺测的数据,保留日观测完整的数据。② 由于积雪深度和降水量同时为零或微量会对模型的建立产生影响,所以剔除降水量和积雪深度同时为零或微量的数据,保留有要么积雪要么有降水的数据。③ 对各台站积雪深度进行了求平均值计算(仅选取有积雪观测资料日期计算平均积雪量),按照日平均积雪将站点从大到小依次排列(表1)。
2.2. 研究方法
本文利用西藏地区35 a逐日气象观测资料对西藏地区积雪深度建立模型:利用日降水量(mm)、平均气温(℃)、最低气温(℃)、最高气温(℃)和积雪深度(cm)、数值预报次日降水量和平均温度为影响因子来建立预测次日积雪深度的多元回归方程(由于缺少数值预报资料,所以用第二天实际观测资料代替数值预报资料),保留通过显著性检验的方程。选取平均积雪最大的五个站点做检验,画出散点图并对相关系数(R)和标准偏差(SEE)进行分析,后改进方法分季节建立积雪深度模型。分析对比改进前和改进后相关系数(R)和标准偏差(SEE)的变化。

Table 1. Basic information of the station in the study area
表1. 研究区站点基本情况
注:*日平均积雪:仅选取有积雪观测资料日期计算平均积雪量。
3. 结果与讨论
3.1. 积雪模型建立
影响积雪深度的主要因子有:降水量、平均温度、最低温度、最高温度、积雪深度、数值预报的次日降水量和平均温度(由于缺少数值预报资料,所以用第二天实际观测资料代替数值预报资料)。
建立用地面观测资料反演的积雪深度多元回归拟合方程:
(6)
式中,y^为模拟值,x1为当日降水量、x2为平均温度、x3为最低温度、x4为最高温度、x5为积雪深度、x6为数值预报的次日降水量、x7为数值预报的次日平均温度。其中b0,b1,b2,b3,b4,b5,b6,b7为回归方程系数,表2为建立的积雪模型系数表。

Table 2. Coefficient table of snow model
表2. 积雪模型系数表
Continued
注:*表示通过90%的显著性检验,**表示通过99%的显著性检验。
3.2. 积雪模型检验
选取日平均积雪深度最大的五个台站(聂拉木、帕里、普兰、错那、嘉黎)进行做散点图2并求相关系数(R)和标准偏差(SEE)进行检验:
五个积雪大站积雪深度模型系数如表3。

Table 3. Coefficient table of snow model at five stations in which daily average amount of snow is largest
表3. 五个积雪大站积雪模型系数表
注:*表示通过90%的显著性检验,**表示通过99%的显著性检验。
五个积雪大站检验散点图如图2,依次是日平均积雪深度从大到小排列的聂拉木、帕里、普兰、错那和嘉黎站,横坐标为观测值,纵坐标为拟合值。从图2中可以看出,五个积雪大站的散点图都为正线性相关关系,日平均积雪深度最大的聂拉木站的散点图模拟值更接近于观测值,即拟合效果最好,而日平均积雪最小的嘉黎站的拟合效果最差。
对五个积雪大站求相关系数(R)和标准偏差(SEE)如表4,虽然相关系数大,但从散点图中仍然可以看出模拟和观测存在误差,需要对模型进行改进。
由于降水、温度等气象要素在不同季节对积雪的形成作用并不一致,所以我们继续分季节对日平均积雪深度最大的五个站点的模型做散点图并求相关系数(R)和标准偏差(SEE)进行检验:
五个积雪大站分季节检验散点图如图3,可以看出每一个站点冬季的拟合效果最好,拟合值最接近观测值,而春秋季的拟合效果则不理想。
表5是五个积雪大站分季节检验相关系数(R),可以看出各站冬季的相关系数明显大于春季的相关系数,说明由于降水和温度对积雪的形成和维持在不同季节作用是不一致的,所以使用一个方程对各站进行拟合并不适合,所以需要对各站分别季节拟合,改进模型模拟结果。

Table 4. Basic test parameters at five stations in which daily average amount of snow is largest
表4. 五个积雪大站检验基本参数

Table 5. Seasonal test of correlation coefficient (R) at five stations in which daily average amount of snow is largest
表5. 五个积雪大站分季节检验相关系数R
3.3. 积雪模型改进
考虑到不同的季节降水和温度对积雪深度的作用结果也有不同,所以对每一个站点分季节求拟合方程进行改进:
分季节重新建模后五个积雪大站积雪深度模型系数如表6。

Table 6. Seasonal coefficient table of snow depth model at five stations in which daily average amount of snow is largest
表6. 五个积雪大站分季节建模后积雪深度模型系数表
Continued
注:*表示通过90%的显著性检验,**表示通过99%的显著性检验。
改进后五个积雪大站分季节散点图如图4,可以看出拟合效果比图3未改进方法分季节散点图的拟合效果更好,拟合值更加接近观测值。
分别计算五个积雪大站改进前和改进后的相关系数R并做折线图进行对比,如表7和图5所示,可以看出改进后相关系数相比改进前相关系数有所增加,说明改进后拟合值更加接近观测值,拟合效果变好。

Figure 5. Comparison of correlation coefficients (R) before/after improvement
图5. 改进前(改进后)相关系数R对比

Table 7. Comparison of correlation coefficients (R) before/after improvement
表7. 改进前(改进后)相关系数R对比
再分别计算五个积雪大站改进前和改进后的标准偏差SEE并做折线图进行对比,如表8和图6所示,可以看出改进后标准偏差相比改进前标准偏差有所减小,这也说明改进后拟合值更加接近观测值,拟合效果变好。

Table 8. Comparison of standard deviation (SEE) before/after improvement
表8. 改进前(改进后)标准偏差SEE对比
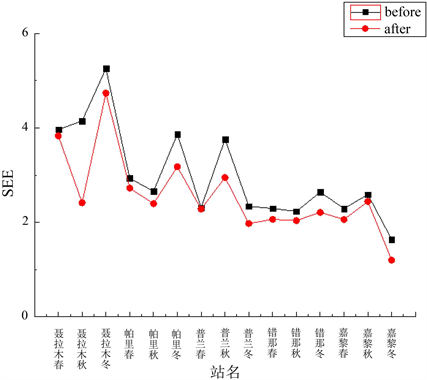
Figure 6. Comparison of standard deviation (SEE) before/after improvement
图6. 改进前(改进后)标准偏差SEE对比
4. 结论
本文利用西藏地区39个气象观测站1979至2013三十五年春、秋、冬三季的地面逐日观测资料,用日降水量(cm)、平均气温(℃)、最低气温(℃)、最高气温(℃)、积雪深度(cm)数值预报次日降水量和平均温度七个影响因子对积雪深度建立模型并进行分析与研究(由于缺少数值预报资料,所以用第二天实际观测资料代替数值预报资料),得到以下结论:
1) 对积雪量不同的台站分别建立模型,可以发现积雪量较大的台站相关系数明显高于积雪量较小的台站,并且积雪量较大的台站拟合效果好于积雪量较小的台站。例如日平均积雪深度最大的聂拉木站的散点图拟合效果最好,而日平均积雪最小的嘉黎站的拟合效果最差。
2) 温度和降水分季节对积雪深度的影响不同,分季节检验后发现拟合值和观测值有较大偏差,说明用同一个方程来分析不同季节的拟合效果并不科学。所以在建立积雪深度模型时不能采用一个观测站建一个模型的方法,要分季节建立模型进行讨论才比较具有可靠性。