1. 引言
利什曼病是由利什曼原虫引起的寄生虫病,利什曼病的两种常见形式是皮肤利什曼病和内脏利什曼病,而内脏利什曼病是两种疾病中较严重的一种,它的标志是肝脏或脾脏内形成肉芽肿。因此研究肉芽肿的形成过程对治疗内脏利什曼病有着积极的意义。本文研究的就是内脏肉芽肿形成的数学模型。该模型是由Nourridine Siewe,Abdul-Aziz Yakubu等人在论文 [1] 提出的,是由抛物型方程和双曲型方程组成的偏微分方程组,模型具体表达如下:
(1.1)
(1.2)
(1.3)
(1.4)
(1.5)
(1.6)
(1.7)
(1.8)
其中,
分别代表促炎巨噬细胞密度,抗炎巨噬细胞密度,促炎巨噬细胞中的寄生虫密度和抗炎巨噬细胞中的寄生虫密度,
代表细胞运动速度,
代表促炎巨噬细胞和抗炎巨噬细胞的死亡比率,
代表促炎巨噬细胞和抗炎巨噬细胞中寄生虫的死亡比率,
代表促炎巨噬细胞和抗炎巨噬细胞中寄生虫的增长系数,
代表促炎巨噬细胞和抗炎巨噬细胞中寄生虫的扩散系数,这些参数均是大于0的参数。
由于
是球对称的,所以
且存在一个标量函数
,使得
。
令
,有
,
。
则问题(1.1)~(1.8)可转化为:
(1.9)
(1.10)
(1.11)
(1.12)
(1.13)
(1.14)
(1.15)
(1.16)
(1.17)
(1.18)
(1.19)
其中,
1999年Friedman和其合作者开始进行关于肿瘤生长模型的严谨数学分析,通过一系列研究,得到了模型整体解和稳态解的存在唯一性 [2] 。随后,出现了大量的数学研究工作者对肿瘤生长自由边界问题的数学分析。参考见 [3] [4] [5] [6] [7] 。根据生物学及医学原理,本文做出以下假设:
(A1)
在
上连续可微,当
时,有
,
,
;
(A2) 当
时,
,且
。
定理1:在条件(A1)~(A2)成立时,对任意的
,问题(1.9)~(1.19)都存在唯一解
,其中
,同时有以下结论成立:
(1.20)
(1.21)
(1.22)
(1.23)
2. 基本引理
首先引进一些基本记号:
1)
,
是
的闭包。
2)
,其范数为
3) 对开集
,记
是
在
的迹空间,
,当且仅当存在
,使得
。当
时,
。
的范数为:
明显地,如果
,则
,且
。
下面介绍本文需要的引理。
引理2.1:设
,
,
分别是
和
的有界连续函数,
是一个常
数,
是
的函数且
,其中
是
的单位球。则下列初边值问题:
(2.1)
(2.2)
(2.3)
有唯一的解
,同时有
其中
是依赖于
的常数,而且对任意的T,
是有界的。更进一步,有
其中若
时,
;否则
,
。
证明:引理2.1的证明可参见 [8] 中的引理4.1的证明。
引理2.2:设
,
,
是
上的有界连续函数,
关于
连续可微,
,则对任意
,则下列初边值问题
(2.4)
(2.5)
(2.6)
有唯一的弱解
,且满足
其中
。当
关于
连续可微,
,则问题(2.4)~(2.6)的弱解是经典解。而且有如下估计成立:
(2.7)
其中当
,
。
当
,有
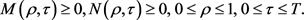 (2.8)
(2.8)
证明:引理2.2的证明可参见 [8] 中的引理4.2的证明。
引理2.3:设
是
的有界连续函数,并且对所有参数都连续,关于
连续可微,
关于
连续可微,
,则下列初边值问题
(2.9)
(2.10)
(2.11)
如果
,则存在
,且T是只依赖于
。
在
上的上确界的常数,使得上述问题(2.9)-(2.11)有唯一的弱解
,同时满足
当
,则上面问题的弱解是经典解。而且有下面估计成立:
(2.12)
其中
。
证明:引理2.3的证明可参见 [8] 中的引理4.3的证明。
3. 局部解的存在唯一性
本节将证明自由边界问题(1.9)~(1.19)存在唯一局部解。
首先,将问题(1.9)~(1.19)转换成固定边界问题。若问题(1.9)~(1.19)有一个解
,且对任意的
,
都成立,则通过如下变换:
(3.1)
问题(1.9)~(1.19)可转换为固定区域为
上的初边值问题:
(3.2)
(3.3)
(3.4)
(3.5)
(3.6)
(3.7)
(3.8)
(3.9)
(3.10)
(3.11)
(3.12)
(3.13)
其中,
反过来,若
是问题(3.2)~(3.13)的解,对任意的
,则通过如下变换:
(3.14)
则可以验证
是问题(1.9)~(1.19)的解,这说明通过变换(3.1)和其逆变换(3.14),自由边界问题(1.9)~(1.19)和固定边界问题(3.2)~(3.13)是等价的。
对方程(3.7)积分,可得:
(3.15)
将(3.15)代入(3.10)可得:
(3.16)
所以,问题(1.9)~(1.19)变换成问题(3.2)~(3.5)和(3.16),同时加上初边值条件(3.8)~(3.9)和(3.11)~(3.12)。
接下来我们将采用压缩映像原理来证明固定边界问题(3.2)~(3.13)局部解的存在唯一性,从而得出自由边界问题(3.9)~(3.19)局部解的存在唯一性。
根据定理1的假设条件(A1)~(A1),则有如下条件成立:
在
上连续可微,对适应的
满足
。
引入记号:
对任意给定的
,引入度量空间
:
由向量值函数
组成,满足:
i)
ii)
iii)
定义
中的度量d为
显然,
是完备度量空间。
定义映射F:
,其中
是下列问题的解:
(3.17)
(3.18)
(3.19)
(3.20)
(3.21)
(3.22)
(3.23)
(3.24)
(3.25)
(3.26)
(3.27)
其中,
(3.28)
(3.29)
下面证明F是一个自映射。首先,对于常微分方程组(3.17)~(3.18),存在唯一解
并且
(3.30)
根据式(3.28)和
的定义可得,
(3.31)
因此
(3.32)
当
充分小,使
时,有
,即
满足条件(i)。
然后,由引理2.1得,问题(3.19)~(3.21)存在唯一解
。因为当
时,
,
所以
。又因为
非负,
,对任意的
都成立。所以
符合条件(ii),同时满足
(3.33)
其中
是依赖于
的常数。同理可证
符合条件(ii),满足
。
最后,由于
关于
连续可微,
连续可微,则由引理2.3可得,问题(3.25)~(3.27)有唯一的经典解
,满足
(3.34)
所以
满足条件(iii),且当
足够小,有
(3.35)
其中,
。
因为条件(i),(ii),(iii)都得到验证,所以当T足够小时,映射F是合理的,是自身到自身的映射。
下面证明F是压缩映射。设
,记
由
,计算得:
(3.36)
接着由(3.30)和(3.36)得:
(3.37)
(3.38)
接着,记
,由(3.19)~(3.21)得,
(3.39)
(3.40)
(3.41)
其中,
。
由于
,
Lipschitz连续的,
,
,所以有
(3.42)
运用引理2.1得,
(3.43)
同理可得
(3.44)
记
,由(3.25)~(3.27)得
(3.45)
(3.46)
(3.47)
其中,
(3.48)
(3.49)
由于
,
Lipschitz连续,
连续可微,
,结合式子(3.34)和(3.35)得
(3.50)
再对问题(3.45)~(3.47)运用引理2.2,可得
(3.51)
因此,根据式子(3.37),(3.43),(3.44)和(3.51)有:
(3.52)
取
充分小,使得
时,F是压缩映射。
由Banach不动点定理可知,当
充分小时,F存在唯一的不动点
,而且它是问题(3.2)~(3.13)在
上的唯一解,再通过逆变换(3.14),就可以将问题(3.2)~(3.13)转换成原问题(1.9)~(1.19)。因此,问题(1.9)~(1.19)存在唯一局部解。
定理2:在假设条件(A1)~(A2)下,存在
,使得问题(1.9)~(1.19)在
上有唯一解,
依赖于
的上下界,
和
的上下界。
4. 整体解的存在唯一性
本节需要对问题(1.9)~(1.19)作先验估计,来研究整体解的存在唯一性。根据(3.16)得,
当
时,如果
,则
,即
。这说明问题(3.2)~(3.13)的解不是对所有的
都成立,因此需要直接考虑变换之前的自由边界问题(1.9)~(1.19)的整体解的存在唯一性。
定理1的证明:
设
为问题(1.9)~(1.19)的解的最大区间,因此只需证明
。采用反证法:设
。首先需证明一些基本结论:若问题(1.9)~(1.19)对所有的
都成立,则有下面的结论成立:
(4.1)
(4.2)
(4.3)
(4.4)
(4.5)
其中
首先,利用抛物型方程的极值原理,可以得到(4.1)式。接着,利用变换
,将
(1.11)~(1.12)的定义域变换成
,利用引理2.2得(4.2)式。再令
,将(1.11)~(1.12)加起来,得
(4.6)
(4.7)
由(4.6)式得,
是问题(4.6)~(4.7)的一个解,由唯一性可知,对任意的
,都有
成立。即(4.3)成立。由(4.2)和(4.3)可得,
。所以
由(1.15)可得,
将上式带入(1.16)可得,
即(4.5)式成立。最后将(4.5)式积分,则有(4.4)式成立。
令
。由(1.12),(1.17)和(1.20)式可知,
是下面问题的解:
(4.8)
(4.9)
(4.10)
其中,
,由已经证明的结论(4.2)~(4.5),可知(4.8)的各项系数都是有界函数,
连续可微有正下界,对问题(4.8)~(4.10)使用引理2.1,可得
,又
,所以
根据
的有界性,可得:对任意的
,都有
同理可得,
而且,由引理2.2可得,
所以,对任意的
,我们考虑有初始时间的
的初值问题(1.9)~(1.19)。根据定理2可知,存在一个一致的
,使得对所有的
,问题(1.9)~(1.19)在
都存在唯一的解。利用唯一性可知,这些解在公共定义的区间上都是相等的,这说明了解可以延拓到
,这与假设
不符合,所以
。因此,定理1得到了证明。