1. 引言
微波滤波是射频(Radio Frequency, RF)系统中的一种重要技术,广泛应用于雷达和通信领域,因此,微波光子滤波技术近年来备受关注 [1] [2] 。由于射频系统逐渐增加的复杂性,微波光子滤波器(Microwave Photonic Filter, MPF)正向高频、高Q值、可重构和可调谐方向发展。与传统的电子滤波器相比,MPF突破了电子器件的带宽限制,在高采样频率、可调谐性、低损耗和抗电磁干扰等方面都具有很大的优势 [3] [4] 。由于其优异的性能,MPF可以满足未来通信领域的大部分需求。
基于无限脉冲响应(Infinite Impulse Response, IIR)的滤波器是MPF的一种典型结构,其原理是利用光纤环提供无数的加权和延迟输入信号,然而这种MPF具有较低的自由光谱范围 [5] 。MPF的另外一种常用结构是基于有限脉冲响应(Finite Impulse Response, FIR)滤波器的,这种结构是以多抽头延迟线为基础的。通常,MPF的光源是由多波长光源或切片宽带光源实现,基于多波长光源的MPF因其高Q值、可调谐性、低噪声而被广泛应用 [6] [7] 。众所周知,在常用的多波长MPF中存在正抽头,通常用作低通滤波器。许多科研工作者通过使用偏振调制 [8] [9] 、交叉增益调制 [10] 、相位调制到强度调制转换 [11] 、多个电光调制器与色散介质相结合 [12] 等实现带通MPF。但是基于偏振调制和相位调制的MPF稳定性能较差;级联FIR滤波器和IIR滤波器的MPF可以用于实现带通滤波 [13] ,本文详细分析了一种级联IIR滤波器和FIR滤波器的MPF,通过调节IIR 滤波器的耦合系数、掺饵光纤环的增益和FBGs的反射率以及FIR滤波器的耦合系数可以实现平坦带通滤波和带阻滤波的互调。
2. 级联IIR滤波器和FIR滤波器的MPF的结构和滤波原理
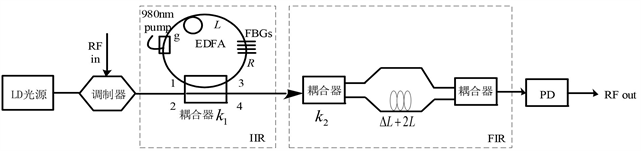
Figure 1. The structure diagram of the microwave photonic filter based on cascaded IIR filter and FIR filter
图1. 级联IIR滤波器和FIR滤波器的MPF的结构图
级联IIR滤波器和FIR滤波器的MPF的结构如图1所示。第一部分是基于掺饵光纤光栅环的IIR滤波器,第二部分是基于M-Z干涉仪的FIR滤波器。调制光通过耦合系数为k1的耦合器,其中的(1− k1)部分光直接进入到FIR滤波器中,剩余的k1部分的光进入长为L的掺饵光纤环中,当经过FBGs时,其中的R部分光被FBGs反射回来,进入耦合器,其中的(1 − k1)部分沿顺时针方向进入掺饵光纤环中,经过掺饵光纤放大器后,在FBGs的另一端再次反射,再经过放大后进入耦合器,其中的k1部分进入FIR滤波器,另外的(1 − k1)部分继续进入掺饵光纤环中传输,如此循环下去。耦合进耦合器k2的光信号通过耦合器k2后被分成两束,其中一束光信号经过M-Z干涉仪上臂后经过耦合器输出,另一束光经过长为
的光纤环后也经过耦合器后输出,其中
的光纤环使两路产生的相位差为
,从而实现FIR微波光子滤波响应。为了使IIR滤波器和FIR滤波器有相同的自由光谱范围,M-Z干涉仪的臂长差减去
后是IIR滤波器光纤环长L的2倍。整个微波光子滤波器由FIR滤波器和IIR滤波器级联形成,通过调节k1、k2、FBGs的反射率R、掺饵光纤环增益g和长度L可以实现MPF不同的滤波性能。
3. 分析和讨论
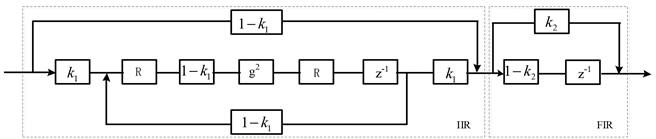
Figure 2. The signal flow diagram of the microwave photonic filter based on cascaded IIR filter and FIR filter
图2. 级联IIR滤波器和FIR滤波器的MPF的信号流程图
根据级联IIR滤波器和FIR滤波器的MPF结构图,可以得到其信号流程图如图2所示,根据信号流程图,利用自动控制原理可以推导出系统函数的表达式:
其中
、
分别是IIR和FIR中耦合器的耦合系数;g为掺饵光纤环的增益;R为FBGs的反射率;
,
是微波信号的基波频率,
是光信号在光纤环中的延迟时间,
为光纤环的
折射率,
为光纤环的长度,
为光速。
3.1. IIR滤波器中耦合器的耦合系数k1对MPF滤波性能的影响
为了理解IIR滤波器中耦合器的耦合系数
对MPF滤波性能的影响,我们计算了当FIR滤波器中耦合器的耦合系数
,掺饵光纤环增益
、长度
,FBGs的反射率R = 0.5,耦合系数
分别为0.3、0.45、0.6时MPF的传输特性曲线,如图3所示,从图中可以看出,MPF的滤波效果均呈现带通响应,主要是由于
保持不变时,FIR滤波器的滤波深度最大,可以实现深度约为50 dB的带通滤波响应 [13] 。而IIR滤波器起到了补偿的作用,所以MPF的传输特性呈现带通响应。从图3可以看出,当
时,补偿效果不好,通带有较大的纹波,而在
时,补偿效果最佳,平坦度最好,随着
的继续增大,补偿效果变差,可能出现了过补偿。
3.2. FIR滤波器中耦合器的耦合系数k2对MPF滤波性能的影响
当固定IIR滤波器中耦合器的耦合系数
,掺饵光纤环增益
、FBGs的反射率R = 0.5,长度
时,FIR滤波器中耦合器的耦合系数
分别为0.2、0.5和0.9时,分析MPF的滤波性能,
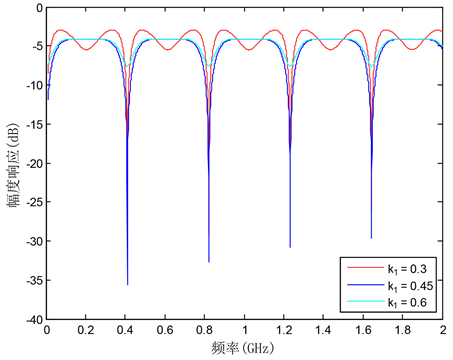
Figure 3. The effect of coupling coefficient k1 with IIR filter on the performance of the microwave photonic filter
图3. IIR滤波器中耦合器的耦合系数k1对MPF滤波性能的影响
如图4所示,可以看到当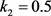 时,实现了平坦的带通滤波性能,而当
和
时,MPF的滤波性能反而呈现出带阻响应。这是因为FIR滤波器在
时具有最大的深度,这时利用IIR滤波器的波谷有效补偿了FIR滤波器的波峰,从而实现平坦的带通滤波响应特性。而改变
为其他值时,FIR滤波器的深度都将变小,此时IIR滤波器的波谷补偿FIR滤波器的波峰,就起到了过补偿的作用,因此呈现出的是带阻响应。
时,实现了平坦的带通滤波性能,而当
和
时,MPF的滤波性能反而呈现出带阻响应。这是因为FIR滤波器在
时具有最大的深度,这时利用IIR滤波器的波谷有效补偿了FIR滤波器的波峰,从而实现平坦的带通滤波响应特性。而改变
为其他值时,FIR滤波器的深度都将变小,此时IIR滤波器的波谷补偿FIR滤波器的波峰,就起到了过补偿的作用,因此呈现出的是带阻响应。
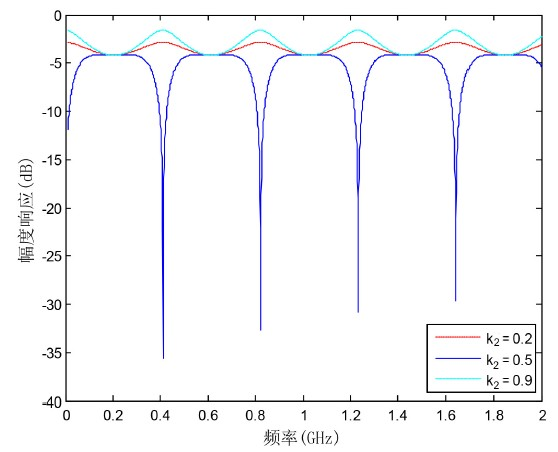
Figure 4. The effect of coupling coefficient k2 with FIR filter on the performance of the microwave photonic filter
图4. FIR滤波器中耦合器的耦合系数k2对MPF滤波性能的影响
3.3. IIR滤波器中的掺饵光纤环的增益g对MPF滤波性能的影响
当固定IIR滤波器中耦合器的耦合系数
,FBGs的反射率R = 0.5,掺饵光纤环长度
,FIR滤波器中耦合器的耦合系数
时,改变掺饵光纤环的增益g分别为1、2、3时,分析其对MPF滤波性能的影响,如图5所示。从图中可以看出,增益g的改变并没有改变MPF的带通滤波特性,这主要是因为FIR滤波器中耦合器的耦合系数
不变,可以实现最大的滤波深度,而IIR滤波器的补偿作用只会改变MPF的平坦度,不会改变其带通滤波特性,因此只会引起MPF滤波幅度的改变。
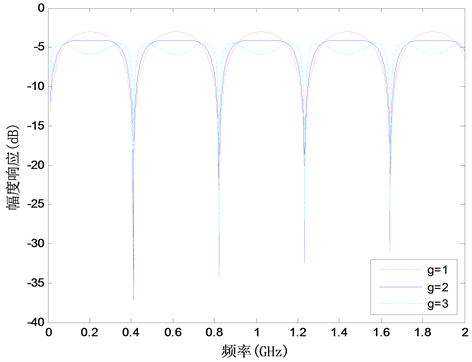
Figure 5. The effect of the gain of the erbium-doped fiber on the performance of the microwave photonic filter
图5. IIR滤波器中掺饵光纤环的增益g对MPF滤波性能的影响
3.4. IIR滤波器中FBGs的反射率R对MPF滤波性能的影响
当固定IIR滤波器中耦合器的耦合系数
,掺饵光纤环的增益g = 2、长度
,FIR滤波器中耦合器的耦合系数
时,改变FBGs的反射率R分别为0.3、0.5、0.7时,分析其对MPF滤波性能的影响,如图6所示。从图中可以看出,反射率R的改变引起滤波性能的变化情况类似于改变掺饵光纤环增益g的情况,这主要是因为FIR滤波器中耦合器的耦合系数
时可以实现最大的滤波深度,而IIR滤波器的补偿作用只会改变MPF的平坦度,不会改变其带通滤波特性。
3.5. 掺饵光纤环的长度L对MPF滤波性能的影响
当固定IIR滤波器中耦合器的耦合系数
,掺饵光纤环增益
,FBGs的反射率R = 0.5,FIR滤波器中耦合器的耦合系数
,改变掺饵光纤环的长度
分别为0.2 m、0.4 m、1 m时,分析其对MPF滤波性能的影响,如图7所示。从图中可以看出,MPF具有很强的边频选择特性,因此可以通过控制光纤环的长度来实现MPF的可调谐性。
3.6. 平坦带阻MPF的实现
当IIR滤波器中的耦合器的耦合系数
,掺饵光纤环增益
,FBGs的反射率R = 1时,IIR滤波器可以实现带阻滤波特性。当FIR滤波器的滤波深度较浅时,即
分别等于0.2、0.4、0.9时分析其
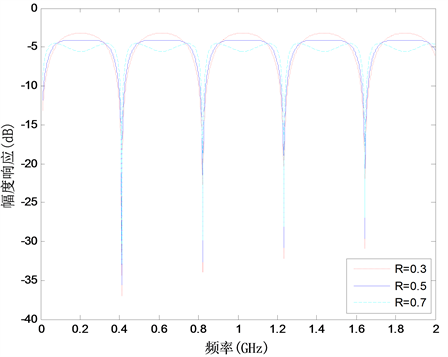
Figure 6. The effect of the reflectivity of the fiber Bragg grating on the performance of the microwave photonic filter
图6. IIR滤波器中FBGs的反射率R对MPF滤波性能的影响
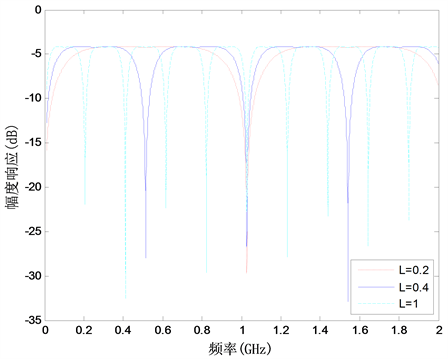
Figure 7. The effect of the length of the fiber ring on the performance of the microwave photonic filter
图7. 掺饵光纤环长度L对MPF滤波性能的影响
对MPF滤波性能的影响,如图8所示,从图中可以看出三组不同
的值都分别实现了平坦的带阻滤波特性。这是因为FIR滤波器只有在
时具有最大的滤波深度,改变为其它值时,FIR滤波器的滤波深度都变得很小,此时IIR滤波器的补偿就起到了过补偿的作用,从而实现的是带阻滤波响应。
4. 结束语
本文给出了一种级联IIR滤波器和FIR滤波器的MPF,根据其结构图,利用自动控制原理得到了该MPF的信号流程图,根据信号流程图计算出系统的传输函数。讨论了IIR滤波器和FIR滤波器的耦合系
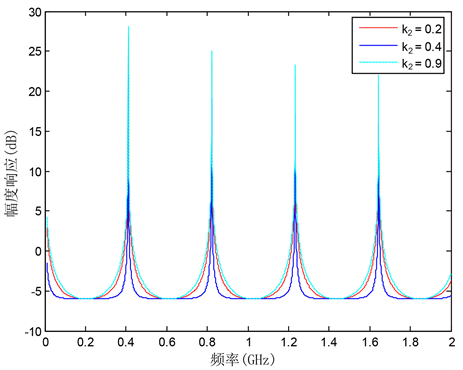
Figure 8. The effect of coupling coefficient k2 with FIR filter on the performance of the bandstop microwave photonic filter
图8. FIR滤波器耦合系数k2对带阻MPF滤波性能的影响
数、FBGs的反射率、掺饵光纤环的增益和长度对MPF滤波性能的影响。通过对IIR滤波器和FIR滤波器中结构参数的分析可知,当
,
,
,
时,可以实现平坦的带通滤波特性;而当
,
,
,
时,可以实现平坦的带阻滤波特性。因此可以通过改变IIR滤波器和FIR滤波器的结构参数实现平坦带通MPF和平坦带阻MPF的互调。
基金项目
贵州省科技厅联合基金项目(黔科合LH字[2016]7036号)、贵州省教育厅青年项目(黔教合KY字[2016]326).贵州省教育厅青年项目(黔教合KY字[2017]360)。