1. 引言
目前关于路基边坡稳定性分析的方法有很多,例如由瑞典人彼得森(K.E. Petterson)提出的以极限平衡理论为基础的条分法和以弹塑性理论为基础的数值计算方法 [1] [2] [3] 。但土中应力–应变关系十分复杂,随着有限元法的提出和发展,越来越多的研究都基于有限元分析,取得了不错的成果 [4] [5] [6] [7] [8] 。但是,边坡稳定性的影响仍然是研究的重点,而对于蜂巢约束系统对路基边坡稳定性的分析仍然不足。为了更好地研究蜂巢约束系统对路基边坡的稳定性的影响,本文基于Drucker-Prager弹塑性模型 [9] [10] [11] [12] [13] ,利用ANSYS建立路基边坡有限元模型,对比附加蜂巢约束系统前后边坡滑动面以及稳定性的差别,分析了蜂巢约束的高度与边坡稳定性关系。基于此研究,能帮助我们更好地了解蜂巢约束在路基边坡中的作用,这为附加约束系统的路基边坡施工提供了技术指导。
2. Drucker-Prager弹塑性模型建立
考虑路基的对称性,取半幅路基结构进行分析。建立ANSYS数值计算模型如图1所示。在边坡上附加蜂巢约束系统,蜂巢通过特定锚杆在边坡上固定。考虑到不同的路基高度及边坡角度,建立了不同尺寸的分析模型,并对比分析边坡附加蜂巢系统前后对路基稳定性及变形的影响。路基计算结构尺寸如表1所示。边坡坡度分别取i = 1.5及i = 1.0。
模型材料参数见表2,包括土体材料参数、蜂巢及锚杆的材料参数。所建立的有限元模型如图2所示。边界条件为左侧对称约束,底边全部约束,右侧边全部约束。分析时采用缩减土体的粘聚力及内摩擦角,来计算边坡的稳定性系数。
3. 蜂巢约束路基对边坡稳定性影响分析
3.1. 无蜂巢约束系统时的边坡稳定性分析
对于表1所示的10种工况,在边坡没有蜂巢约束系统时进行了边坡稳定性分析。不同工况情况下的

Figure 1. Numerical calculation of model size
图1. 数值计算模型尺寸
边坡破坏滑动面如图3所示。从图中可以看出,在不同的边坡角度情况下,在路基高度较低时,边坡失稳的滑动面起自路基顶面而终于坡角处;而当路基较高时,边坡失稳的滑动面起自路肩至坡角处所构成的三角形区域,出现了三角形的滑移区。
不同边坡角度情况下,边坡稳定性系数与路基高度的关系见图4所示。可以看出,在边坡角度一定的情况下,路基边坡的稳定性系数与边坡的高度成正比,随着边坡高度的增加,边坡的稳定性系数降低;在路基高度一定的情况下,随着边坡角度的减小,边坡的稳定性增加。
3.2. 有蜂巢约束系统时边坡稳定性分析
对于表1所示的10种工况,在边坡附加了蜂巢约束系统时进行了边坡稳定性分析。不同工况情况下的边坡破坏滑动面如图5所示。从图中可以年看出,在不同的边坡角度情况下,在附加了蜂巢系统之后,不同高度及不同角度情况下的边坡失稳滑动面与没有蜂巢系统的情况下相比发生了变化,滑动面的下缘一般出现在坡角下方,与没有蜂巢的情况相比,边坡的稳定性由于蜂巢的存在得到了提高。并且滑动面均通过路基顶面,没有出现三角形的滑移区。
不同边坡角度情况下,边坡稳定性系数与路基高度的关系见图3~9所示。在边坡附加蜂巢系统之后,在边坡角度一定的情况下,路基边坡的稳定性系数与边坡的高度成正比,随着边坡高度的增加,边坡的稳定性系数降低;在路基高度一定的情况下,随着边坡角度的减小,边坡的稳定性增加。
3.3. 蜂巢约束系统对边坡稳定性的影响分析
不同边坡坡度情况下,边坡附加蜂巢之后,边坡的稳定性系统如图7所示。在边坡坡度i = 1.5时,在附加了蜂巢之后,边坡的稳定性系数分别增加了4.7%~5.9%。在边坡坡度i = 1.0时,在附加了蜂巢之后,边坡的稳定性系数分别增加了15.8%~20%。由此可见,在边坡角度较小,即边坡较陡时,附加蜂巢系统之后,可以更为明显的提高边坡的稳定性。
不同的边坡坡度情况下,附加蜂巢约束系统(格栅)前后,路基顶面及边坡顶面的竖向变形如图8~图17所示。从图中可以看出,在附加了蜂巢系统(格栅)之后,在路基顶面的竖向变形方面,蜂巢系统可以减小路基失稳滑动面区域内的路基顶面变形,而对滑动区域以外的路基顶面的竖向变形没有影响;在边坡顶面的竖向变形方面,蜂巢系统可以减小边坡顶部的竖向变形,尤其对边坡较陡的情况更为明显。在边坡坡度i = 1.0时,附加了蜂巢系统之后最大可以减小14.8%的坡顶竖向变形。因此,在边坡较陡的情况下,附加蜂巢可以提高边坡的稳定性。
4. 降雨对蜂巢约束路基边坡稳定性的影响分析
水渗透路基中之后,会增加土的容重,减小土的粘聚力及内摩擦角,因而会影响到边坡的稳定性。
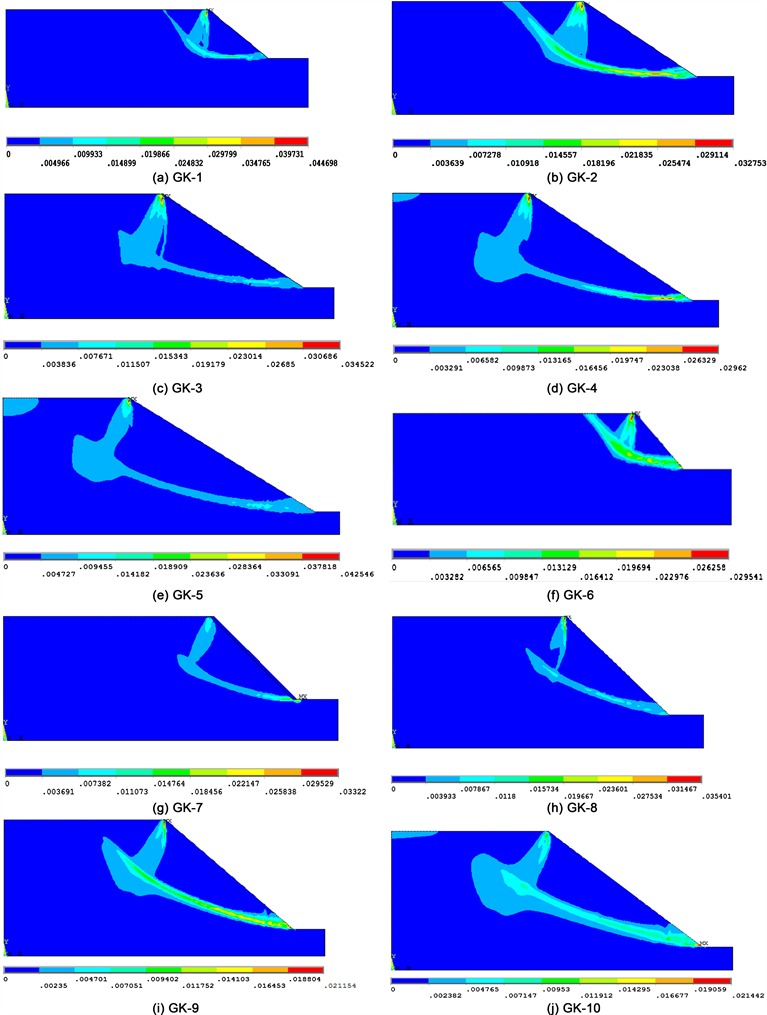
Figure 3. The sliding surface of a slope when it becomes unstable
图3. 边坡失稳时的滑动面
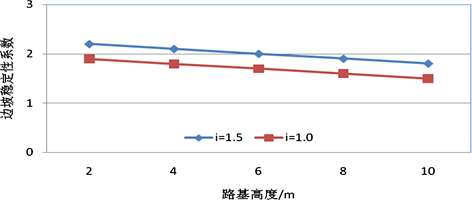
Figure 4. Relationship between subgrade slope stability and subgrade height
图4. 路基边坡稳定性与路基高度的关系

Figure 5. Slope instability sliding surface with honeycomb system
图5. 有蜂巢系统时的边坡失稳滑动面
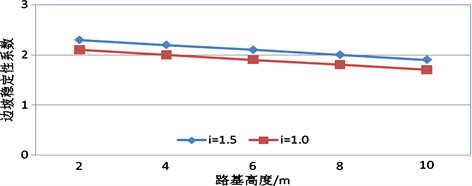
Figure 6. The relationship between subgrade slope stability and subgrade height with honeycomb system
图6. 有蜂巢系统时路基边坡稳定性与路基高度的关系
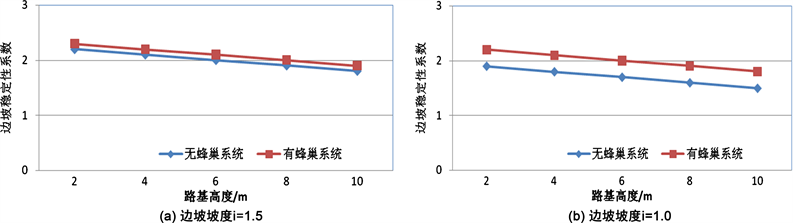
Figure 7. Influence of honeycomb restraint system on slope stability
图7. 蜂巢约束系统对边坡稳定性的影响
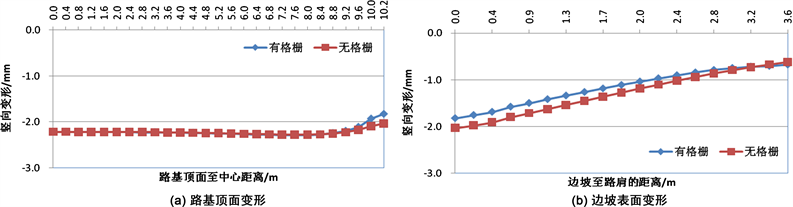
Figure 8. Influence of honeycomb restraint system on slope deformation (GK-1)
图8. 蜂巢约束系统对边坡变形的影响(GK-1)
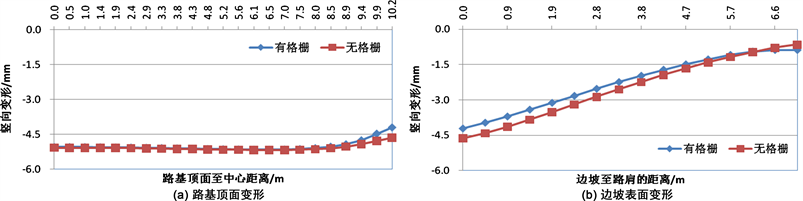
Figure 9. Influence of honeycomb restraint system on slope deformation (GK-2)
图9. 蜂巢约束系统对边坡变形的影响(GK-2)
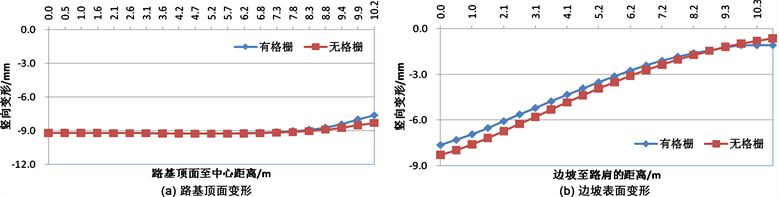
Figure 10. Influence of honeycomb restraint system on slope deformation (GK-3)
图10. 蜂巢约束系统对边坡变形的影响(GK-3)
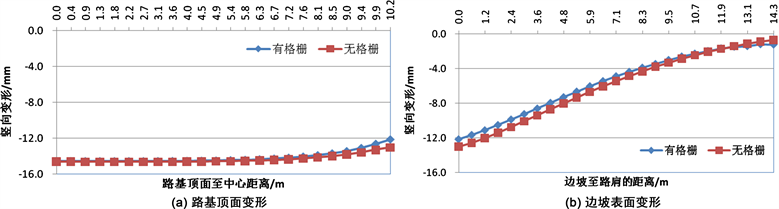
Figure 11. Influence of honeycomb restraint system on slope deformation (GK-4)
图11. 蜂巢约束系统对边坡变形的影响(GK-4)
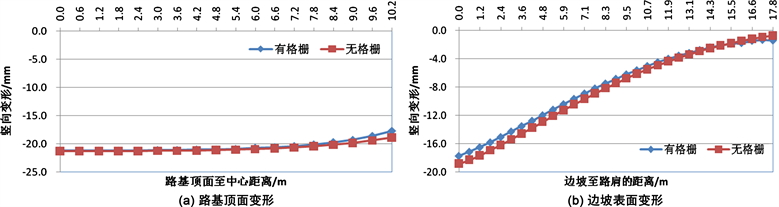
Figure 12. Influence of honeycomb restraint system on slope deformation (GK-5)
图12. 蜂巢约束系统对边坡变形的影响(GK-5)
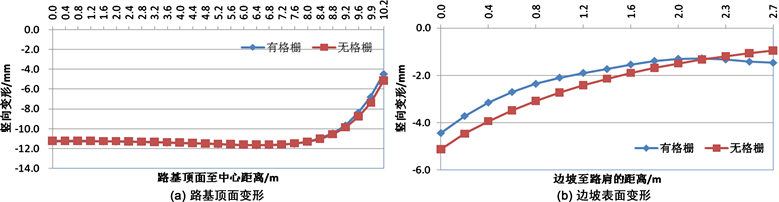
Figure 13. Influence of honeycomb restraint system on slope deformation (GK-6)
图13. 蜂巢约束系统对边坡变形的影响(GK-6)
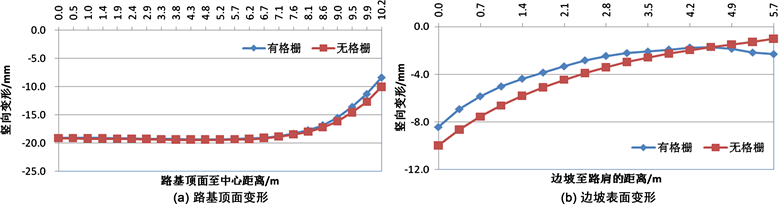
Figure 14. Influence of honeycomb restraint system on slope deformation (GK-7)
图14. 蜂巢约束系统对边坡变形的影响(GK-7)
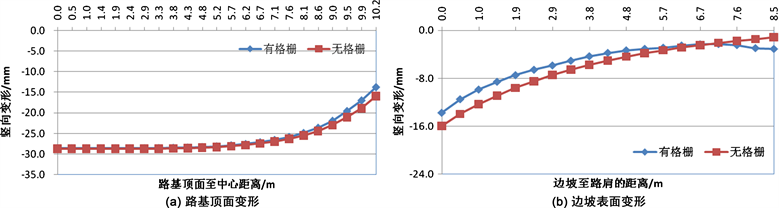
Figure 15. Influence of honeycomb restraint system on slope deformation (GK-8)
图15. 蜂巢约束系统对边坡变形的影响(GK-8)
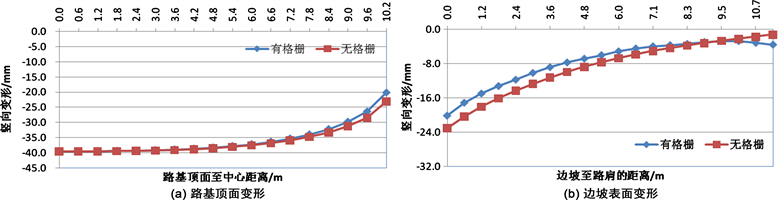
Figure 16. Influence of honeycomb restraint system on slope deformation (GK-9)
图16. 蜂巢约束系统对边坡变形的影响(GK-9)
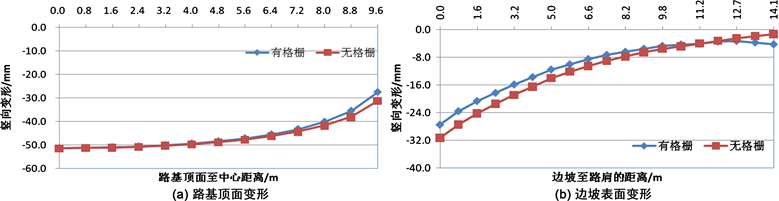
Figure 17. Influence of honeycomb restraint system on slope deformation (GK-10)
图17. 蜂巢约束系统对边坡变形的影响(GK-10)
本部分考虑路基浸水之后的情况,浸水后路基土的材料参数见表3。

Table 3. Material parameters of subgrade soil soaked in water
表3. 浸水路基土的材料参数
对于高度6 m的路基进行了浸水路基的稳定性进行分析,分别分析了不同的边坡角度,即GK-3及GK-8两种工况。不同情况下的边坡滑动面如图18所示。浸水条件下边坡滑动面均为通过路基顶面及坡角的圆弧滑动面。浸水情况的路基的边坡稳定性系数见表4。从表4中可以看出,路基浸水之后,路基土的容重增加,粘聚力及内摩擦角均减小,路基边坡的稳定性下降,发生路基失稳的可能性增加,这时通过在边坡附加蜂巢可以提高浸水路基的边坡稳定性。

Table 4. Slope stability coefficient of soil-soaked subgrade
表4. 浸水路基土的边坡稳定系数

Figure 18. Slope instability sliding surface under different conditions
图18. 不同情况下的边坡失稳滑动面
5. 蜂巢结构尺寸对边坡稳定性的影响分析
本部分分析蜂巢约束系统的高度对边坡稳定性的影响,选取蜂巢的高度分别为5 cm、10 cm、15 cm、20 cm进行仿真分析。选取前述的工况8进行计算。不同蜂巢高度时得到的边坡失稳滑动面如图19所示。不同高度的蜂巢系统情况下,边坡失稳的滑动状态相同。
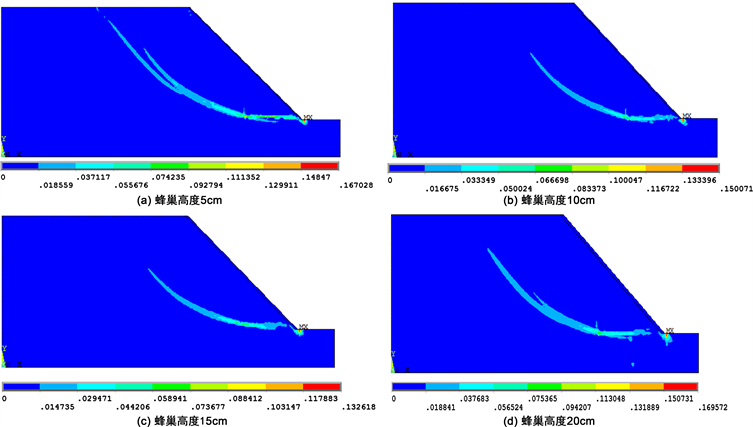
Figure 19. Slope instability sliding surface at different honeycomb heights
图19. 不同蜂巢高度时的边坡失稳滑动面
边坡稳定性系数与蜂巢系统高度的关系如图20所示。从图中可以看出,在蜂巢高度为5 cm时,蜂巢对边坡的稳定性没有加强作用,这时与没有蜂巢系统时的边坡稳定性系数相同,随着蜂巢高度的增加,边坡的稳定性系数呈现线性的增加趋势,因此在考虑边坡稳定的情况下,在参照蜂巢系统材料成本的前提下,应尽量选用较高的蜂巢约束系统,这样可以取得较好的边坡稳定效果。

Figure 20. Relationship between slope stability coefficient and honeycomb height
图20. 边坡稳定性系数与蜂巢高度的关系
6. 结论
本文建立了边坡稳定性分析的数值模型,对比分析了边坡附加蜂巢约束系统对于边坡稳定性的影响。分析了不同路基高度、不同边坡角度及浸水情况对路基稳定性的影响规律。对比分析了边坡失稳滑动面的变化及路基竖向变形的变化规律。
1) 对比无约束的边坡,边坡附加蜂巢约束系统后,边坡失稳滑动面由坡脚处移动到坡脚前,并且滑动面均通过路基顶面,没有出现三角形的滑移区。同时,边坡坡度i = 1.5时,边坡的稳定性系数分别增加了4.7%~5.9%;在边坡坡度i = 1.0时,边坡的稳定性系数分别增15.8%~20%,边坡的稳定性有明显提高。
2) 其次,研究发现,蜂巢系统可以减小路基失稳滑动面区域内的路基顶面变形,而对滑动区域以外的路基顶面的竖向变形没有影响,尤其对边坡较陡的情况更为明显。在边坡坡度i = 1.0时,附加了蜂巢系统之后最大可以减小14.8%的坡顶竖向变形。
3) 最后,在研究蜂巢高度对边坡稳定性影响时发现,在蜂巢高度为5 cm时,蜂巢对边坡的稳定性没有加强作用,这时与没有蜂巢系统时的边坡稳定性系数相同,随着蜂巢高度的增加,边坡的稳定性系数呈现线性的增加趋势,因此在考虑边坡稳定的情况下,在参照蜂巢系统材料成本的前提下,应尽量选用较高的蜂巢约束系统。