1. 引言
随着无线通信产业的迅速发展,移动通信已经迈入5G时代,无线移动通信系统及相关技术正经历一个高速发展的时代。而更高通信容量的宽带通信技术背后,是很多诸如OFDM以及MIMO等非恒定包络调制方式的应用,这些信号具有宽频带以及较高的频谱利用效率,对功率放大器(PA)的线性度提出较高要求。
PA作为无线通信系统的关键组成部分,其功能是将已调信号放大到所需功率并经天线发射。PA符合晶体管特性,在放大区内PA呈现线性,而随着输入信号功率的增加,PA将呈现非线性特性。同时随着带宽增加,记忆效应(即功放当前输出同时取决于当前的输入信号以及过去时刻的输入信号)也较为突出。PA的记忆非线性效应会导致通信信号的失真,带内误码率升高,带外频谱扩展,通信质量下降等问题 [1] 。为避免此类问题,常采用数字预失真技术对功率放大器的记忆非线性进行补偿,为保证对具有记忆效应的功率放大器非线性失真的补偿性能,数字预失真器的特性应与功率放大器的非线性特性及记忆特性完全相反,这些特性需通过建立功率放大器行为模型进行准确描述,功率放大器行为建模的本质是非线性系统辨识问题。
近年来不少国内外学者对记忆功率放大器的行为模型进行大量研究,提出诸如Winner模型及Hammerstein模型等用以描述功率放大器的非线性记忆效应,而鉴于功率放大器和数字预失真本身的一些特点,基于Volterra级数的模型得到最广泛的研究和应用,Volterra级数能较为全面地描述一个非线性系统 [2] ,但由于其模型复杂度非常高,参数数目庞大,研究者提出各类简化或改进Volterra级数模型,诸如2006年A. Zhu提出的DDR-Volterra级数 [3] 等模型。而模型参数的获取需要对模型进行辨识,1997年,Changsoo Eun首次提出基于间接学习结构的预失真估计结构,大量参数估计算法可以应用于预失真系统中 [4] 。常用的辨识算法有最小二乘法(LS),Kwong于1992年提出的经典变步长最小均方法(LMS) [5] ,递归最小二乘法(RLS)以及卡尔曼滤波法。
针对功率放大器非线性特性引入的非线性失真问题,本文对功率放大器的预失真补偿技术进行研究,建立基于Volterra级数的预失真器数学模型,分别采用LS,RLS,LMS,Kalman滤波算法对Volterra预失真器进行参数辨识,以最小均方误差作为衡量指标,对四种算法进行参数优化,进而构建出有效的Volterra预失真器。
2. 功率放大器与预失真器技术
2.1. 功率放大器的非线性记忆特性
在工程应用中,通常期望功率放大器具有理想的线性增益,但理想功率放大器在实际中并不存在,功率放大器符合晶体管特性,在放大区内呈线性,而随着输入信号功率增加,功率放大器将呈现非线性。功率放大器非线性特性在时域中通常采用幅度–幅度调制转换(AM-AM)及幅度–相位调制转换(AM-PM),分别指输入幅度变化导致的输出幅度及相移的非线性变化。AM-AM失真与AM-PM失真能对非线性系统进行较直观的描述,AM-AM失真主要研究输入信号与输出信号幅度上的非线性失真特性,AM-PM失真主要表现在输出信号与输入信号的相位上。
功率放大器的AM-AM及AM-PM特性仿真图如图1所示。
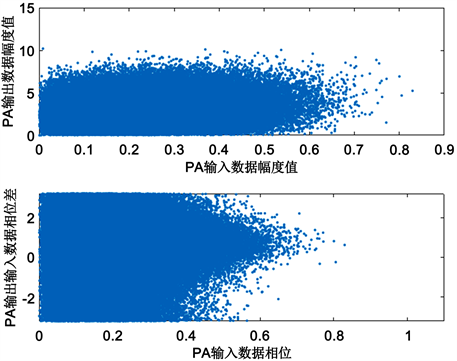
Figure 1. AM-AM and AM-PM feature simulation
图1. AM-AM及AM-PM特性仿真
从图中可以看出,输入信号经功率放大器放大后,幅度并不是线性放大,并且输出信号与输入信号相位差不为0,即功率放大器具有非线性放大的特性。同时实际功率放大器总存在一定程度的记忆效应,即指功率放大器当前输出同时取决于当前的输入信号以及过去时刻的输入信号,在宽带通信系统中,功率放大器呈现出显著的记忆非线性。
为对功率放大器非线性记忆特性进行更好描述,需建立功率放大器模型。依据建模方式及目的不同,功率放大器的模型可分为物理模型和行为模型,其中物理模型是依据电路、元件相互关系并利用基本电路定律形成非线性方程,适合电路级仿真,但物理模型需要较多器件内部详细信息并且计算复杂度高。不同于物理模型,行为模型属于“黑箱”模型,不需要很多器件内部信息,可通过实验数据进行模型建立并利用该模型对功率放大器行为特性进行描述及分析。Saleh函数结构简洁,能利用较少参数实现功率放大器非线性记忆特性的描述,应用有记忆特性的Saleh函数模型 [6] 如式(1):
(1)
其中,
为输入信号
的相角,
分别为功放AM-AM和AM-PM特性拟合参数,分别为:
利用FIR滤波器首先对输入信号进行处理,再引入Saleh函数模型,即为有记忆特性的Saleh模型。
2.2. 预失真技术原理
预失真技术即在功率放大器前端构造一个与其特性相反的非线性系统,输入信号经该非线性系统产生非线性特性,抵消功率放大器的非线性失真实现整个系统的线性化,从模型上可将预失真器看为功率放大器的逆模型。预失真器置于功率放大器之前,系统结构功能示意图如图2所示。
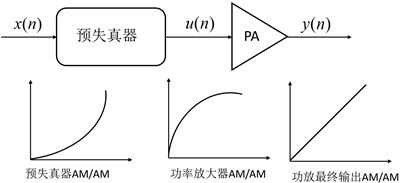
Figure 2. Schematic diagram of predistortion technology
图2. 预失真技术原理示意图
3. 预失真器的数学模型
预失真模型为与功率放大器模型特性相反的非线性多项式模型,主要有以下几类。
3.1. Wiener模型
Wiener模型具有两箱式结构,由一个线性子系统和一个无记忆非线性系统级联而成,结构示意图如图3所示。

Figure 3. Schematic diagram of the Wiener model structure
图3. Wiener模型结构示意图
若非线性子系统由多项式形式实现,线性子系统经FIR滤波器实现,输出可表示为 [7] :
(2)
其中,M表示FIR滤波器的长度,h(m)表示FIR滤波器单位脉冲响应,α2k−1为多项式的系数,K为多项式最高阶数。
3.2. Hammerstein模型
Hammerstein模型与Wiener模型的结构相对称,可视作Wiener模型的逆模型,由一个无记忆非线性(NL)子系统与一个线性时不变级联而成,结构示意图如图4所示。

Figure 4. Schematic diagram of the Hammerstein model structure
图4. Hammerstein模型结构示意图
若非线性子系统由多项式形式实现,线性子系统经FIR滤波器实现,则输出可表示为:
(3)
其中,M表示FIR滤波器的记忆长度,h(m)表示FIR滤波器单位脉冲响应,α2k−1为多项式的系数,K为多项式最高阶数。
3.3. Volterra级数模型
Volterra级数是Taylor幂级数的扩展,相当于在Taylor级数的基础上增加记忆项,它能较为全面地描述一个非线性系统并描述其记忆特性,非常适合动态非线性系统的建模,在记忆非线性功率放大器及数字预失真建模中得到非常广泛的应用,其时域表达式如式(4):
(4)
其中,
称为Volterra级数的n阶内核,同时也被称为n阶非线性冲激响应,离散域表达式为 [8] :
(5)
式中,
是输入输出信号的复包络,
是k阶离散Volterra级数核,k表示Volterra级数模型的非线性阶数,M表示Volterra级数模型的记忆深度,反映功率放大器记忆特性的大小。
由于Volterra级数模型能较为全面地描述一个非线性系统并描述其记忆特性,非常适合动态非线性系统的建模,本文应用全内核的Volterra级数模型对预失真器进行建模,通过参数辨识算法对其进行参数辨识,以抵消功率放大器的非线性放大特性。
4. Volterra预失真器模型辨识
4.1. 预失真器参数辨识
由于预失真器和功率放大器具有相反非线性特性,从系统辨识角度考虑,二者并无本质差别,用于功率放大器的模型同样可适用于预失真器的建模,但数字预失真器在系统参数辨识方面要比功率放大器部分要复杂,预失真器位于功率放大器前端,无法获得该系统理想输出信号,一般可先对功率放大器进行建模,再通过反馈和学习对预失真器进行模型建立和参数辨识。预失真器反馈学习结构大概可分为直接学习结构和间接学习结构,预失真器直接学习结构系统示意图如图5所示。

Figure 5. Predistorter direct learning structure
图5. 预失真器直接学习结构
其中,x(n)表示输入信号,经预失真器得信号u(n),预失真器输出信号送入功率放大器PA中得到功率放大器输出信号y(n),设功率放大器增益为G,对y(n)进行G倍衰减反馈至预失真器输入端进行参数辨识。预失真器间接学习结构如图6所示 [9] 。

Figure 6. Predistorter indirect learning structure
图6. 预失真器间接学习结构
间接学习结构无需辨识功率放大器的行为模型,而是假设一个在结构上与预失真器完全相同的后失真器,在其中进行参数辨识,并把辨识参数复制到预失真器。对于功率放大器系统,若存在后失真器,则也存在唯一和后失真器等同的预失真器,若通过间接学习结构能辨识出后失真器,则该后失真器即为预失真器。预失真器的参数辨识算法主要有LS算法、RLS算法、LMS算法以及Kalman滤波算法。
4.2. 最小二乘算法(LS算法)
最小二乘算法 [9] 通过求实际值y(k)与模型计算值
之差平方和达最小的参数值作为最小二乘法的解,误差平方和可表示为:
(6)
LS算法参数估计值
满足:
(7)
将输入以及参数均用向量形式表示:
(8)
则输出y(k)可表示为:
(9)
y(k)的向量表达式也可用矩阵表示:
(10)
式中,
,
。
则最小均方误差可表示为:
(11)
若
为满秩矩阵,可得最小二乘解为:
(12)
4.3. 递归最小二乘法(RLS算法)
LS算法是通过计算矩阵
一次处理所得。递归算法指在每取得一新数据时,就根据此数据对原估计量进行修正得到新的估计量。引入一个加权因子
对式(6)进行修正:
(13)
其中,
称为遗忘因子,
。
RLS算法是通过
时刻数据去估计n时刻数据。最常用的递归最小二乘算法为:
(14)
式中
,
为权系数矩阵。
4.4. 最小均方算法(LMS算法)
RLS算法简化形式为:
,用
代替增益矩阵
即为LMS算法:
(15)
其中
为步长参数,满足
,
为输入信号
特征值的最大值。LMS算法是一种搜索算法 [10] ,其算法如下:
(16)
4.5. 卡尔曼滤波算法(Kalman滤波算法)
卡尔曼滤波算法利用目标动态信息,设法去掉噪声的影响,得到关于目标位置的良好估计。其基本思想是利用前一时刻的状态估计值和当前时刻的观测值获得动态系统当前时刻状态变量的最优估计。
由
时刻参数辨识值
预测N时刻的参数辨识值
,有:
(17)
由前一次协方误差
以及噪声Q预测新误差
:
(18)
卡尔曼增益的计算式为:
(19)
其中,λ为遗忘因子。接着进行模型辨识结果的校正更新如式(20):
(20)
并更新P值如式(21):
(21)
5. 仿真分析
本文通过MATLAB对功率放大器及预失真器进行模型仿真,仿真实验样本信号为OFDM信号,基带带宽为2 MHZ,射频带宽为4 MHZ。OFDM即正交频复用技术,是多载波方案的实现方式之一,其主要思想是将信道分为若干正交子信道,将高速的数据信号转化成并行低速子数据流,分别调制到每个子信道中进行传输,每个子信道带宽仅为原信道带宽的一小部分,信道均衡相对容易。
仿真以均方误差(MSE)为指标衡量模型的准确性,均方误差指实际值与模型计算值之差平放的期望,均方误差定义式为 [11] :
(22)
MSE越小表示模型精确有更好的精确度。
本文借助LS、RLS、LMS和Kalman滤波算法对预失真器模型分别进行参数识别,取Volterra非线性阶数K为3,记忆深度M为6,分别利用四种算法进行参数辨识,信号经过预失真器和功率放大器后的功率谱密度如图7所示。

Figure 7. Comparison of power spectral densities obtained by different parameter identification algorithms
图7. 不同参数辨识算法功率谱密度比较
各自的均方误差如表1所示。

Table 1. Model accuracy for different algorithm identification
表1. 不同算法辨识模型精度
于图7可看出,Kalman滤波算法辨识得到的功率谱密度边带较低,并且最小均方误差非常小。而LMS算法在此条件下参数辨识能力较差,并且步长参数
随数据的改变稳定性较差。
其次,对实验数据引入已知信噪比的高斯白噪声,分别利用四种算法进行模型参数辨识。引入信噪比为30 dB的白噪声,辨识效果如图8,表2所示。

Figure 8. Power spectral density of a signal passing through DPD and PA at 30 dB noise
图8. 30 dB噪声时信号经过DPD与PA后的功率谱密度

Table 2. Model accuracy for different algorithm identification
表2. 不同算法辨识模型精度
若引入信噪比为20 dB的高斯白噪声,四种辨识算法如图9,表3所示。

Figure 9. Model output power spectral density at 20 dB noise
图9. 20 dB噪声时模型输出功率谱密度

Table 3. MSE of model identification at 20 dB noise
表3. 引入20dB噪声模型辨识均方误差
在15 dB至40 dB以5 dB为间隔引入高斯白噪声,利用四种算法进行模型辨识,做出均方误差与信噪比的关系图线如图10所示。

Figure 10. MSE of the model under different noise conditions
图10. 不同噪声情况下模型均方误差
由图10可看出,引入不同信噪比的高斯白噪声后,四种算法辨识效果都有一定的影响。其中,LS算法在信噪比为30 dB时参数辨识性能达到极限,其参数辨识性能不会再随输入信号信噪比的增加而提高;RLS算法辨识效果随噪声引入性能下降较为明显;LMS算法辨识效果受噪声影响较小,但其辨识能力与其他辨识算法相比非常有限,无噪声时模型辨识均方误差仅为−25.7961 dB;Kalman滤波算法具有较好的参数辨识效果,无噪声时辨识均方误差可达−68.6391 dB,并且随输入信号信噪比的不断增加,其参数辨识性能会不断地改善。综上所述,Kalman滤波算法具有更好的稳定性和模型辨识能力,RLS算法在噪声环境下辨识能力较差,LMS算法虽然辨识能力有限,但其在噪声环境下依然有较好的辨识稳定性。经Kalman滤波算法辨识后的系统AM-AM,AM-PM特性如图11所示。
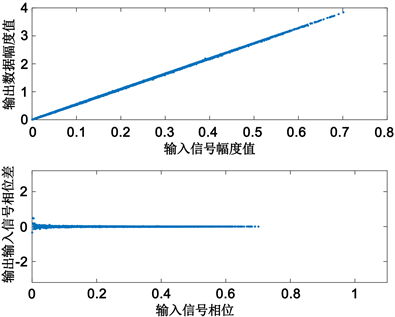
Figure 11. Amplification characteristics of DPD-PA identified by Kalman filtering algorithm
图11. Kalman滤波算法辨识的DPD-PA放大特性
如图11所示,引入预失真器(DPD)补偿的功率放大器AM-AM与AM-PM特性较图1有很好的改善,输出信号幅度值为输入信号幅度值的线性放大,输出信号与输入信号的相位差近似为0,说明预失真模型能够很好地补偿功放的非线性放大特性。
6. 结论
本文对功率放大器记忆非线性自适应预失真技术进行研究,建立基于全内核Volterra级数的自适应预失真模型,借助LS、RLS、LMS和Kalman滤波算法对全内核Volterra预失真模型的内核进行参数辨识并以最小均方误差(MSE)作为指标对四种算法进行深度优化。仿真结果表明,Kalman滤波算法具有最优的参数辨识精度,辨识最小均方误差可达−68.6391 dB;在噪声环境下,基于Kalman滤波自适应预失真器依然能够有效地补偿功率放大器的记忆非线性。本文为进一步理解和研究无线通信系统的自适应预失真技术提供参考,并对模型参数辨识算法的改进提供一定的参考价值,为之后采用改进的Kalman滤波算法以及压缩感知(Compressed sensing)算法进行更高精度的参数辨识打下基础。
NOTES
*通讯作者。