1. 引言
随着能源和环境问题的逐步突显,风能作为商业化开发利用最具有潜力的新能源,越来越受到各国的重视 [1] [2] [3] [4] 。基于常规能源的发电计划的制定,可靠性能够得到保障,发电功率预测水平和容量可信度较高,但是由于风电本身波动性较强的特点使得其容量可信度较低,可预测性较差,发电计划制定较为困难,同时风电并网加大电网调度难度,对电网运行产生不利影响。因此对风电功率进行准确的预测是保障电网安全稳定运行的前提。
风电功率预测一般分为超短期、短期和中长期预测 [5] [6] 。其中超短期预测一般指4 h以内的预测,结果用于安排调度计划等,预测方法主要为依赖历史数据的统计方法,因此数据质量成为一个不可忽视的问题。一个时间序列被采集时不可避免的会受到人为或非人为的噪声干扰,比如数据采集和传输装置的震荡或者故障,使得真实的时间序列波动发生改变。噪声往往是叠加在真实时间序列上的毛刺,具有频率高幅值低的特点,对噪声部分很难进行预测,且准确预测对整体的预测精度提升有限。因此对风电功率序列进行去噪具有一定的工程实用价值,常见的去噪方法有小波分解、经验模态分解等,文献 [7] 通过离散小波变换将信号分解为高低频段的信号,再用遗传算法优化的BP神经网络分别进行建模,最后求和各层预测信号;文献 [8] 采用小波包分解理论对经过初步处理的历史风速数据进行分解处理,根据相关性剔除随机数据,利用不同结构的Elman神经网络寻找最优分解树不同频段下的风速规律得到预测结果;文献 [9] 提出了一种基于经验模态分解的预测模型,针对分解出的不同分量建立不同的预测模型,进而提高预测精度。上述方法信噪分解区分难度大,一些突变的细节容易被去除,并且小波分解层数与去噪阈值无法被确定。
风电功率预测统计方法通常为时间序列分析方法和人工智能方法,例如持续法、自回归滑动平均、人工神经网络和支持向量机等。持续法是将上一时刻的功率真实值作为下一时刻的预测值,具有简单易实现的优点,但不具备突变信息处理能力。时间序列主要是利用历史的风电功率数据进行统计分析,推测出风电功率变化趋势,进而实现风电功率的预测。神经网络和支持向量机是最为常见的人工智能模型预测方法,通过大量的训练集训练确定变量的对应关系,建立确定的预测模型实现预测。上述预测方法都采用单一的预测模型,在很大概率上出现较大的预测偏差,具有一定的局限性。因此采用组合预测法成为一种研究趋势。文献 [10] 提出一种基于小波变换和神经网络的组合预测方法,对小波分解序列分别建立神经网络模型实现预测;文献 [11] 采用交叉熵理论对不同的单一预测模型进行组合,组合后的预测精度得到提高;文献 [12] 提出动态组合预测方法来进行风电功率的预测,但组合算法单一。上述方法中组合成员权重自适应调整能力差,预测精度存在进一步提高的空间,且有效的组合提高预测精度的本质在于增加样本信息,降低不确定性。
本文提出一种基于奇异谱分析去噪和加权系数动态修正的风电功率实时组合预测模型。利用奇异谱分析将风电出力序列分解成有限个子序列,将风电功率时间序列的功率谱密度波峰的个数作为重构子序列个数的分配依据,得到消噪序列,剩余分量作为噪声滤除,对消噪序列采用最小二乘法辨识公式对单一预测结果进行权重的动态组合,计算得到最终的预测结果。算例分析表明,该方法能够有效预测风电出力,具有良好的普适性。
2. 奇异谱分析
奇异谱分析(Singular spectrum analysis, SSA)是一种全局分析法,主要用于信号的分解与去噪,能够识别趋势、周期或准周期、噪声信号成分。该方法具体步骤如下:
1) 嵌入。设长度为N的一维时间序列
,给定正整数L为滑动窗口长度,
,建立轨迹矩阵,可以表示为:
(1)
2) 奇异谱分解。对轨迹矩阵X进行奇异谱分解,得到:
(2)
其中d为X的非零奇异值个数。
3) 分组。通常认为前r (r < d)个较大奇异值反映有用信号成分,后d - r个较小的奇异值被认为是噪声成分。这样,分组的操作就是确定合适的r值,从而实现信噪分离。
4) 对角平均化。实现矩阵转化为一维时间序列
的功能。重构序列可通过下式(3)获得,原序列由重构部分叠加如下式(4)计算得到:
(3)
(4)
SSA在计算过程中有两个参数需要输入,即L和r,对重构序列进行分析确定
[13] ,此时重构误差最小;原始信号的功率谱密度的主频谱个数n,选取
[14] 。SSA能够对时间序列进行分解,将最可预报的分量集中分布到若干个具有重要意义的分量中进行重建,将噪声信号筛选出,从而实现信噪分离。
3. 加权系数动态修正组合模型
组合预测是利用一定的方法将不同的单一预测方法进行组合,不是简单的归集,而是得到最佳的预测结果的融合,最为常见的组合预测方法为平均权值组合法,其表达式为:
(5)
式中:Pt为t时刻的组合预测值;pit为第i个单一预测方法在t时刻的预测值;n为单一预测方法数目。
该方法简单,但不能充分挖掘预测方法的各自的积极信息。故提出一种动态权重修正的方案,以各单一预测方法为输入,实际风电功率为:
(6)
式中:Pt是t时刻的组合预测结果;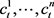 为组合权值;
为单一预测方法在t时刻的结果;n为预测方法个数;ct为常数项,平衡系统误差。
为组合权值;
为单一预测方法在t时刻的结果;n为预测方法个数;ct为常数项,平衡系统误差。
实现组合预测的关键是获得组合权值。本文采用最小二乘法辨识公式中的组合系数确定权值,对权值进行实时更新与修正。以均方根误差最小为目标,于是有:
(7)
式中:Tjt为第j天t时刻的实际出力;d为临近历史样本窗宽。
将公式(6)带入公式(7)中可得:
(8)
ct为第t时刻的预测组合权值,求取Q对ct的极值点,下一时刻,更新历史数据,重新计算权值,实现权值的动态实时修正,保持组合效果最佳状态,将计算得到的权值代回公式(7),得到最终的风电出力预测结果。
以风电场的实际风电功率序列为例,装机容量为265.5 MW,采样间隔为15 min,采用三种单一预测方法,记为P1、P2、P3,并且与平均组合权值、动态权值组合比较,预测结果见图1,误差情况见表1,所分析的误差指标包括准确率r1、均方根误差r2、平均绝对误差r3,上述误差评价指标如式(10)、(11)、(12)。
由图1和表1可以看出,各个单一预测方法的预测误差特点不同,P1与P2变化相对缓慢不能识别出上升与下降的趋势,P3能够很好的识别出上升与下降的趋势,但可能变化过于剧烈而导致误差变大,平均组合权值的预测准确率低于动态权重组合,说明平均权值组合不能充分挖掘单一预测模型的成员信息,组合预测效果提升有限,通过动态权值组合对组合权重进行修正,能够充分挖掘单一预测模型的成员信息,预测精度显著提高,组合更加合理。

Table 1. Relative error of forecasting results
表1. 预测结果相对误差
4. 基于奇异谱分析去噪和加权系数动态修正的风电功率实时组合预测模型
风电功率数据采集过程中不可避免的会受到干扰而混入噪声,对噪声进行准确预测对整体预测贡献小,从而使得预测方法很难得到准确的预测结果。且风本身的波动性与间歇性特点,导致风电功率相对比常规能源的预测困难,现有的预测方法对于相对平稳序列预测结果较好,对于波动明显的时间序列预测精度较差,风电功率时间序列的变化规律很难掌握,尤其是多步预测时,单一方法的预测精度很难达到要求。由于奇异谱分析方法可以去除时间序列中的噪声分量,对序列进行重构,在噪声处理中体现了突出的优势,并且组合预测方法可以弥补单一预测方法的缺陷,动态修正权重能够充分挖掘各组合成员的积极信息,有效提高预测精度,因此本文提出了一种基于奇异谱分析去噪和加权系数动态修正的风电功率实时组合预测模型。具体的建模步骤如下:
1) 原始风电功率时间序列F经过奇异谱分析的嵌入、分解、分组和对角平均化最终得到重构后的风电功率时间序列Y;
2) 对重构后的时间序列Y分别建立单一预测模型,各单一预测模型输出结果是
;
3) 根据
建立第t预测时刻下组合权值的求解方程,其中
,风电实际出力
,并求解出权值系数
。
4) 将步骤(3)求得的第t预测时刻下的权值系数引入公式(6),便可计算获得未来第t预测时刻下的组合预测结果;
5) 下一时刻重新启动奇异谱分解与组合预测模型,更新训练样本数据,重复步骤(1)至步骤(4),对权值进行动态修正,完成下一时刻的预测。
5. 算例分析
5.1. 数据来源
选择东北某3个风电场的风电出力实测数据作为数据来源。本文主要研究实时预测,并以整场出力为研究对象,采样间隔为15 min。通过对多个不同装机容量大小的风电场数据进行研究,验证本文方法具有一定的普遍适应能力。3个电场的装机容量见表2。

Table 2. Installed capacity of wind farm
表2. 风电场装机容量
5.2. 评价指标
选取准确率、均方根误差、平均绝对误差三个指标对预测效果进行评价,三个指标的表示形式如下:
1) 日平均预测计划曲线准确率r1
(9)
(10)
2) 全天预测结果均方根误差r2
(11)
3) 全天预测结果平均绝对误差r3
(12)
上面的三个指标中,各个变量的具体含义如下:
r1i为第i次实时预测的准确率;
为第i次实时预测中第k个时刻的实际功率;
为第i次实时预测中第k个时刻的预测功率;Cap为风电场装机容量。
5.3. 实验结果
以装机容量为265.5 MW的风电场C为例对本文模型进行测试,选取其中某一天为研究对象进行奇异谱分析去噪,获得重构后的序列,原始风电出力如图2所示。
本文采用Welch法来获取功率谱密度,该方法误差较小,功率谱估计更加平滑。所得的功率谱密度如图3所示。
从图3可以发现在低频处存在一个主频,其他频率没有发现峰值,该时间序列的功率谱密度的主频数为1,根据上述介绍得知重构信号的个数为2,前2个重构成分叠加作为消噪序列,剩余成分作为噪声序列滤除。确定合适的重构奇异值个数,从而实现信噪分离。奇异值贡献率如图4所示。

Figure 2. Curve: original wind power output
图2. 原始风电出力

Figure 3. Curve: power spectral density of wind power sequence
图3. 风电功率序列的功率谱密度
Figure 4. Curve: eigenvalue contribution rate
图4. 特征值贡献率
第一个奇异值的贡献率为96.23%,第二个奇异值的贡献率为1.719%,剩余的贡献率均小于1%,因此选择前2个奇异值对序列进行重构是合理的,原始序列、重构序列和残差序列如图5所示。

Figure 5. Curve: diagram of original sequence, reconfiguration sequence and residual sequence
图5. 原始序列、重构序列和残差序列图
根据奇异谱方法对风电功率时间序列进行分解,得到有限个子序列,然后将风电功率时间序列的功率谱密度波峰的个数作为重构子序列个数的分配依据,得到消噪序列,剩余分量作为噪声滤除,实现了对原始风电功率序列的去噪。
为验证奇异谱分析的优越性,与传统的小波阈值去噪进行比较,选取某三天的风电出力为研究对象,原始序列、小波阈值去噪与奇异谱分析去噪的时间序列如图6所示。
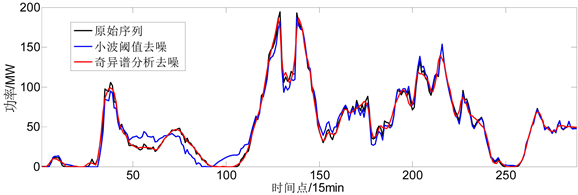
Figure 6. Curve: schematic diagram of original sequence, wavelet threshold denoising and singular spectrum denoising analysis
图6. 原始序列、小波阈值去噪与奇异谱分析去噪的时间序列示意图
奇异谱分析去噪更贴近原始序列,将毛刺滤去,而小波去噪与原始序列部分位置具有较大偏差,为验证去噪的合理性,分别对原始序列、小波阈值去噪与奇异谱分析去噪的时间序列采用本文所提组合预测的方法进行预测,预测的误差结果情况见表3。

Table 3. Forecasting error results
表3. 预测的误差结果
可以发现对奇异谱分析去噪的序列进行预测,能有效提高预测精度,预测的各项指标均优于传统的小波阈值去噪,验证了奇异谱分析能够有效实现信噪分离,且去噪对提高预测精度具有一定的作用。
在奇异谱分析去噪的基础上,对去噪序列进行单一预测,采用本文所提方法对单一预测建立动态权值组合预测模型,其中随机选取1天的各单一预测方法的自适应组合权值如图7所示。
各个单一预测方法的权值系数波动剧烈,说明充分挖掘了单一预测模式的信息,实现有效组合。将本文动态权值组合与平均权值组合方法、单一预测方法进行对比,计算误差评价指标,结果如表4所示。

Table 4. Forecasting error results of C wind farm
表4. 风电场C预测结果误差
动态组合预测结果的准确率为91.02%,比采用平均组合权值预测准确率结果改善了0.95个百分点,比P1、P2与P3准确率分别提高了0.44%、0.76%、3.15%,且动态组合权值预测的平均绝对误差比平均组合权值降低了0.97个百分点,比P1、P2与P3平均绝对误差分别降低了0.32%、0.68%、3.61%,减少了较大误差的出现,验证了动态权重组合的有效性。平均权值的固定组合预测方法准确率结果低于P1与P2的预测方法,说明平均权值的固定方法权值分配不合理,不能实现有效组合,导致预测效果更差。
为进一步验证方法有效性和普适性,选取装机容量不同的风电场A和B进行测试,同样采取历史3天的数据进行奇异谱分析去噪,并对重构序列建立单一预测模型,提取单一预测结果数据,分别计算平均权值与动态权值,得到最终的预测结果。对比未去噪与奇异谱去噪以及对比平均权值组合与动态权值组合,随机展示一天的预测结果误差如表5、表6所示。

Table 5. Forecasting error results of A wind farm
表5. 风电场A的预测结果误差

Table 6. Forecasting error results of B wind farm
表6. 风电场B的预测结果误差
从表中可以看出,装机容量不同的风电场在采用四种方法进行实时预测时,去噪之后的预测结果比未去噪的预测结果好,说明奇异谱分析选取前几个较大的奇异值对时间序列进行重构,获得消噪序列,剩余序列作为噪声去除,能够有效的区分信号和噪声,对消噪序列进行预测能够提高预测精度,同时对权值进行动态修正,能够有效挖掘预测模型的信息,各项指标均优于平均权值组合方法,本文所提出的奇异谱分析去噪和加权系数动态修正的组合预测方法的预测效果均优于其他预测方法,展示出了良好的预测性能。
6. 结论
风电时间序列在采集过程会混入噪声,对预测准确度产生一定的影响,并且针对传统组合权值赋值方法的局限性,提出了基于奇异谱分析去噪和加权系数动态修正的风电功率实时组合预测模型。通过风电场实测数据进行验证,算例结果表明将原始风电功率序列进行奇异谱分析,得到重构后的消噪序列,实现信噪分离,再对消噪序列进行预测,进而提高了预测精度。动态权值组合预测的平均绝对误差最小,预测精度高于平均权值组合,说明能够减少较大误差的出现,实现单一预测方法的有效组合,并且用不同装机容量的风电场验证了本文模型的普适性。
参考文献