1. 引言
相位解缠是合成孔径雷达干涉测量数据处理的重要步骤之一。自Goldsterin等人在1988年提出所谓的枝切法以来,各种基于InSAR数据的相位解缠算法不断涌现,这些方法大致可以分为两大类。一类是路径跟踪算法 [1] [2] [3] ,如Goldstein枝切法等。另一类是非路径跟踪算法 [4] [5] [6] ,如最小LP范数法等。前者是一种局部算法,其优点是可以隔绝相位不连续点,阻止局部相位误差在整个积分区域的传播,计算速度较快,在相干性较好的区域可以获得精确的解缠相位,但是在强噪声条件下,很难获得最佳积分路径,容易造成误差传递或无法解缠的孤立区域。后者则是一种全局算法,其优点是运算稳定性好,不需要识别残差点。除了上述两大类算法外,利用最优估计算法如网络流模型 [7] 、卡尔曼滤波模型 [8] [9] [10] 等进行相位解缠也受到越来越多的关注。文献 [8] [9] [10] 采用卡尔曼滤波模型,将相位解缠转化为状态估计问题,通过建立相位的动态方程和观测方程求解真实相位,实现相位解缠与噪声消除的一并处理。
常规卡尔曼滤波相位解缠算法中观测方程的噪声方差由相干图的值确定,本文分别应用伪相干图、相位导数方差图和最大相位梯度图的值来确定噪声方差,采用扩展卡尔曼滤波进行相位解缠。在地形平坦和陡峭两种条件下对真实InSAR数据进行实验,通过对解缠结果进行对比分析,表明对于地形陡峭数据应用相位导数方差图得到的结果较可靠,而地形平坦数据应用伪相干图能够得到较为精确的解缠结果。
2. 三种质量图
2.1. 伪相干图
当幅度值为单位值1时,伪相干图的值定义为:
(1)
式中k为视数,
是由干涉数据提取的干涉相位值。
2.2. 相位导数方差图
相位导数方差图是描述相位梯度变化的图像,其值定义如下:
(2)
这里,点
在以点
为中心
窗口内的取值,
和
是相位偏导数,
和
是相位偏导数在
窗口内的均值。
2.3. 最大相位梯度图
最大相位梯度图中值的定义为两个相位梯度值中的较大值:
(3)
这里,
和
是相位偏导数。
3. 卡尔曼滤波相位解缠基本原理
卡尔曼滤波的观测方程为:
(4)
式中,
表示复干涉,
表示观测干涉振幅,
为真实相位,
为
和
间的非线性映射。
为零均值高斯白噪声,其方差已知,应用质量图的值 来确定,即:
来确定,即:
(5)
这里,
为Kronecker函数。
卡尔曼滤波的状态空间模型为:
(6)
这里,A为给定状态空间模型的系统矩阵,
,
分别表示真实相位梯度及相位梯度估计,
为估计误差。
卡尔曼滤波相位解缠的递推方程为:
(7)
式中,
和
分别表示预测值及其对应的方差阵,
为相位梯度估计,
为状态噪声方差阵,
和
分别表示状态估计及其对应的方差阵,
是滤波增益矩阵,
是残差,
表示线性化的观测矩阵。
4. 实验结果与分析
4.1. 地形陡峭条件下的实验结果与分析
采用ENVISAT卫星分别在2003年12月3日和2004年
1 月 7 日
获取的2景伊朗Bam地区图像作为实验的主副图像,通过干涉、配准、去平地效应等处理后,从中选取地形起伏较大的部分干涉图(100像素 × 100像素)如图1所示。图2~4分别为应用相位导数方差图、伪相干图和最大相位梯度图进行卡尔曼滤波相位解缠得到的结果。从解缠结果上看,伪相干图的解缠结果较差,最大相位梯度图和相位导数方差图均能得到较高精度的解缠相位。这是因为在地形比较陡峭的区域,伪相干图对梯度变化较为敏感,将坡度变化大的区域作为噪声区域处理,不能准确地进行相位解缠。图5为对应的三种质量图。
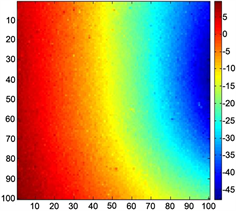
Figure 2. Phase derivative variance unwrapped result
图2. 相位导数方差解缠图
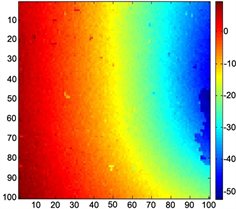
Figure 3. Pseudo-coherence coefficient unwrapped result
图3. 伪相干系数解缠图
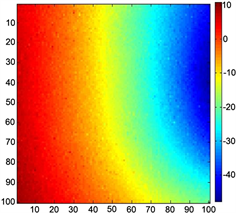
Figure 4. Maximum phase gradient unwrapped result
图4. 最大相位梯度解缠图
 (a)
(a) 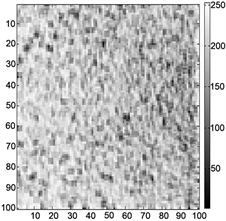 (b)
(b)  (c)
(c)
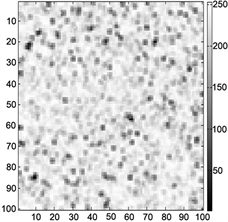
Figure 5. (a) Phase derivate variance map; (b) Pseudo coherence map; (c) Maximum phase gradient map
图5. (a) 相位导数方差图;(b) 伪相干图;(c) 最大相位梯度图
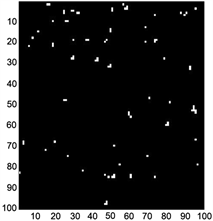
由三种质量图解缠结果得到的不连续点图如图6所示。从图6可以看出,应用伪相干图的解缠结果在低质量相位区域出现了较多的不连续点,相位导数方法图和最大相位梯度图的不连续点分布大致相同,较好地消除了噪声。
 (a)
(a) 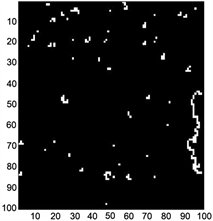 (b)
(b)  (c)
(c)
Figure 6. (a) Phase derivative variance discontinuous points map; (b) Pseudo-coherence coefficient discontinuous points map; (c) Maximum phase gradient discontinuous points map
图6. (a) 相位导数方差不连续点图;(b) 伪相干系数不连续点图;(c) 最大相位梯度不连续点图
下面从不连续点数目和ε值这两个方面对解缠的结果进行定量分析。ε值越小,解缠质量越高;不连续点数目越少,抗相位畸变的性能越好。从表1可以看出,在地形陡峭条件下,相位导数方差图解缠结果的不连续点数目明显少于其他两种方法,滤波效果优于最大相位梯度图和伪相干图,抗相位畸变性能较强。ε表达式 [11] 为:
(8)
其中,M和N分别为列数和行数。
是点
处的解缠相位。
和
是与缠绕相位梯度
和
相对应的权重,而此权重一般由相位质量图给出,其值一般在0到1之间。p的取值通常有0,1,2。这里,p取1。从ε值来看,相位导数方差图解缠结果的解缠质量略高于最大相位梯度图和伪相干图,解缠结果较可靠。

Table 1. Three quality maps phase unwrapping results’ number of discontinuous points and ε value
表1. 三种质量图相位解缠的不连续点数目和ε值表
4.2. 地形平坦条件下的实验结果与分析
采用ENVISAT卫星分别在2005年1月30日和2005年3月6日获取的2景山东济宁地区图像作为实验的主副图像,经过干涉处理后取其地形较为平坦的干涉图(100像素 × 100像素)如图7所示。
三种质量图的解缠结果如图8~10所示。从解缠结果可以看出应用伪相干图进行卡尔曼滤波相位解缠可以得到比较精确的结果,最大相位梯度图和相位导数方差图得到的解缠结果较差,这是因为后两种质量图在进行相位解缠时将地形平坦数据表征为低质量区域,故得到可靠性较差的解缠结果。图11为与干涉图对应的三种质量图。
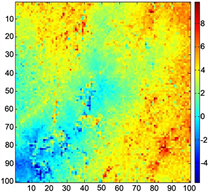
Figure 8. Phase derivative variance unwrapped result
图8. 相位导数方差图解缠结果
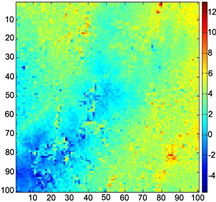
Figure 9. Pseudo-coherence coefficient unwrapped result
图9. 伪相干图解缠结果
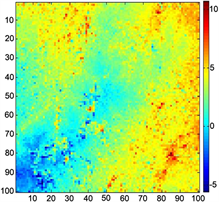
Figure 10. Maximum phase gradient unwrapped result
图10. 最大相位梯度图解缠结果
 (a)
(a) 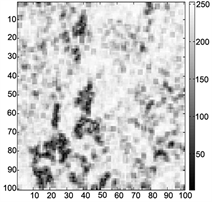 (b)
(b) 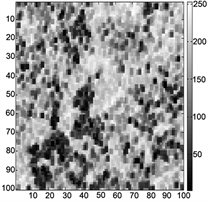 (c)
(c)
Figure 11. (a) Phase derivate variance map; (b) Pseudo coherence map; (c) Maximum phase gradient map
图11. (a) 相位导数方差图;(b) 伪相干系数图;(c) 最大相位梯度图
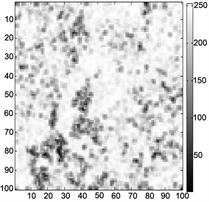
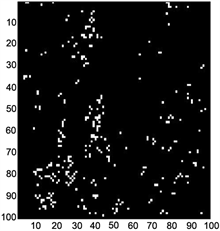
根据解缠结果得到的不连续点图如图12所示,从不连续点图可以看出在高质量区域三种解缠结果的不连续点分布大致相同;在低质量区域,伪相干图的不连续点分布略好于最大相位梯度图和相位导数方差图,说明伪相干图的滤波效果较好。
 (a)
(a)  (b)
(b) 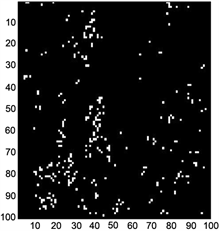 (c)
(c)
Figure 12. (a) Phase derivative variance discontinuous points map; (b) Pseudo-coherence coefficient discontinuous points map; (c) Maximum phase gradient discontinuous points map
图12. (a) 相位导数方差不连续点图;(b) 伪相干系数不连续点图;(c) 最大相位梯度不连续点图
从表2可以看出,伪相干图解缠结果的不连续点数目明显少于最大相位梯度图和相位导数方差图,表明伪相干图消除噪声的能力较强;而ε值略低于相位导数方差图和最大相位梯度图,说明伪相干图解缠的精度较高。综合不连续点数目和ε值来看,对于地形较为平坦的数据,在没有相干图的情况下,首先应该选择伪相干图作为质量图。

Table 2. Three quality maps phase unwrapping results’ number of discontinuous points and ε value
表2. 三种质量图相位解缠的不连续点数目和ε值表
5. 结论
应用三种质量图分别确定卡尔曼滤波相位解缠算法中的观测噪声方差,对地形陡峭和平坦两种条件下的InSAR实际数据进行相位解缠。解缠结果表明,不同的地形条件下选取的质量图也应不同。地形陡峭数据选取相位导数方差图作为质量图能够得到可靠的解缠结果,而地形平坦数据应用伪相干图得到的解缠结果较为精确。
参考文献