1. 引言
基于Huber [1] 1989年混沌控制及Pecora and Carroll [2] 1990年混沌同步的开创性工作,混沌控制与同步吸引了大量系统理论研究工作者的广泛兴趣和关注。控制问题重点研究混沌吸引子的稳定化(使之呈现周期运动或静止状态),而同步可视为特殊的控制问题,当今研究核心在于跟踪特定的混沌运动,并使两类混沌系统达到运动的一致性。研究方法表现为线性控制技术与非线性控制技术 [3] 。本文运用非线性反馈方法研究了一类分数阶混沌差分方程的同步问题。
2. 系统模型
本文考虑如下差分方程
(1)
当
时,系统有长时记忆,表现为演化过程中依赖于过去所以状态。而当v = 1时,则为经典的Logistic模型。文献 [4] 讨论了如下的非线性控制问题
(2)
其中K与P为控制刚度,x为主控制量而y为从控制量。但我们发现文 [4] 所给参数不能达到同步。
为此我们考虑了系统(2)主系统
与从系统
的同步问题,即
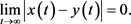
3. 主要结果
引入误差变量
误差系统变为
 (3)
(3)
而根据Caputo-型差分 [4] [5] [6] 定义,系统(3)可写为
其中
为左Caputo-型delta差分,
为离散时间尺度
(
,本文取
)。
显然同步状态依赖于控制刚度K,P及控制目标x。此外若P = 1,则可根据文 [6] 定理38可得如下结论。
定理1:假定P = 1,
。若方程
(4)
的根全部落在单位圆内。则系统(2)中主系统 与从系统
达到同步,即,
。
与从系统
达到同步,即,
。
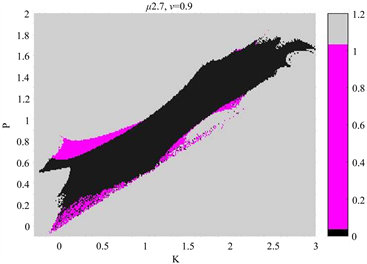
进一步我们运用Matlab软件包给出如下数值结果。图一中黑色区域表示为同步区域(其中
),灰色区域为非同步区域(其中误差
),而有色区域为过渡状态。在图1 (3)中,我们用一条有色的线画出了当P = 1且v = 1时同步区域。与定理1对应结论(
)吻合。说明我们数值结果的准确性。
 (1)
(1)
 (2)
(2)
 (3)
(3)
Figure 1. Nonlinear feedback chaotic synchronization for fractional-order Logistic difference equation with initial conditions x(0) = 0.2, y(0) = 0.3 and parameters
图1. 分数阶Logistic差分方程的非线性反馈混沌同步研究,其中初始条件x(0) = 0.2,y(0) = 0.3及参数
4. 结论
本文运用非线性反馈方法研究了一类分数阶混沌差分方程的同步问题,建立了一类混沌映射同步的判别准则,给出数值模拟结果,验证了理论分析的准确性,并推广了已有文献结果。
基金项目
山东省自然科学基金资助(ZR2015AL004)。