一个新五维超混沌系统的分析与电路设计

Analysis and Circuit Design of a Novel 5D Hyperchaotic System

摘要: 本文研究一个新的五维自治超混沌系统，借由系统的对称性、耗散性、平衡点特性和初值敏感性，分析其动力学特性。给出新五维超混沌系统的Lyapunov指数及数值仿真相轨迹曲线，以此说明超混沌吸引子的存在性。本文采用超混沌电路改进型模块化设计方法设计出新五维超混沌系统的模拟电路模型。模拟电路模型仿真产生的超混沌相轨迹曲线定性表明电路仿真结果与数值仿真结果的一致性，以及所设计的模拟电路模型的正确性。

Abstract: A novel five-dimensional (5D) autonomous hyperchaotic system is studied in this paper. The dy-namics are analyzed, including the symmetry, dissipation, equilibrium point characteristics and initial value sensitivity. The Lyapunov exponents of the novel 5D hyperchaotic system, as well as the phase portraits of the numerical simulation, are shown to prove the existence of the hyperchaotic attractors. The analog circuit model is designed via the modified module-based approach to hyperchaotic circuit design. The hyperchaotic phase portraits of the analog circuit model are also given to illustrate the good qualitative agreement between the numerical simulation results of the mathematic model and the circuit simulation results of the analog circuit model, which would demonstrate the correctness of the analog circuit model.

1. 引言

1963年，美国气象学家Edward Lorenz首先发现混沌运动 [1] 。混沌运动具有丰富而复杂的非线性动力学特性，其在信号处理、保密通信、生命科学等领域具有重要的应用价值和前景，一直是非线性领域的研究热点之一 [2] [3] [4] 。混沌运动通常发生在三维及以上的非线性自治系统中。混沌运动的主要特点包括：初值敏感性、有界性、自相似性、分数维和遍历性。当系统可产生混沌运动时，一般具有一个正的Lyapunov指数、一个等于零的Lyapunov指数、其余均为负的Lyapunov指数。

1979年，德国物理学家Otto Rössler首先提出超混沌的概念以及超混沌Rössler系统 [5] 。超混沌运动具有混沌运动的所有性质和一切特征，且具有更为复杂的非线性动力学行为，其在自然科学、电子通信以及其他工程应用领域中较之混沌运动更具有优势，因此也更具有研究价值和应用前景 [6] [7] [8] [9] 。超混沌运动与混沌运动的主要区别为：

1) 超混沌运动通常发生在四维及以上的非线性自治系统中；

2) 超混沌系统的维数是三维以上的分维数；

3) 超混沌系统具有两个或两个以上正的Lyapunov指数。

由于超混沌运动具有以上特性和研究优势，本文作者于文献 [10] 中提出一个新五维超混沌系统，但未对其非线性动力学特性进行详细分析。因此，针对该新五维超混沌系统，本文拟从对称性、耗散性、平衡点特性和初值敏感性四个方面出发分析其动力学特性，借助Matlab数值仿真软件，计算新五维超混沌系统的Lyapunov指数和Lyapunov维数，绘制系统的数值仿真相轨迹曲线，以此说明系统中超混沌吸引子的存在性。在此基础上，本文拟采用超混沌电路改进型模块化设计方法设计新五维超混沌系统的模拟电路模型，借助Multisim电路仿真软件，绘制系统的电路仿真相轨迹曲线，并将其与数值仿真相轨迹曲线逐一进行对比，以此定性说明所设计的新五维超混沌系统的模拟电路模型的正确性。

2. 新五维超混沌系统的动力学特性分析

2.1. 数学模型

新五维超混沌系统的数学模型如下所示 [10]

$\begin{array}{l}\frac{\text{d}x}{\text{d}t}=a\left(y-x\right),\\ \frac{\text{d}y}{\text{d}t}=\left(c-a\right)x+cy+w-xz,\\ \frac{\text{d}z}{\text{d}t}=-bz+xy,\\ \frac{\text{d}v}{\text{d}t}=mw,\\ \frac{\text{d}w}{\text{d}t}=-y-hv,\end{array}$ (1)

其中， $x,y,z,v,w\in ℝ$ 为系统的状态变量， $a=23$ ， $b=3$ ， $c=18$ ， $m=12$ ， $h=4$ 为新五维超混沌系统(1)的典型参数。

2.2. 对称性

将系统(1)中的x、y、v、w替换为 $-x$ 、 $-y$ 、 $-v$ 、 $-w$ ，可得

$\begin{array}{ccc}\begin{array}{l}\frac{\text{d}\left(-x\right)}{\text{d}t}=a\left[\left(-y\right)-\left(-x\right)\right],\\ \frac{\text{d}\left(-y\right)}{\text{d}t}=\left(c-a\right)\left(-x\right)+c\left(-y\right)+\left(-w\right)-\left(-x\right)z,\\ \frac{\text{d}\left(+z\right)}{\text{d}t}=-bz+\left(-x\right)\left(-y\right),\\ \frac{\text{d}\left(-v\right)}{\text{d}t}=m\left(-w\right),\\ \frac{\text{d}\left(-w\right)}{\text{d}t}=-\left(-y\right)-h\left(-v\right),\end{array}& \begin{array}{l}\\ \\ \to \\ \\ \end{array}& \begin{array}{l}\frac{\text{d}x}{\text{d}t}=a\left(y-x\right),\\ \frac{\text{d}y}{\text{d}t}=\left(c-a\right)x+cy+w-xz,\\ \frac{\text{d}z}{\text{d}t}=-bz+xy,\\ \frac{\text{d}v}{\text{d}t}=mw,\\ \frac{\text{d}w}{\text{d}t}=-y-hv,\end{array}\end{array}$

即通过坐标变换 $\left(x,y,z,v,w\right)\to \left(-x,-y,z,-v,-w\right)$ ，系统(1)的数学模型不发生改变，故新五维超混沌系统(1)关于z轴对称。

2.3. 耗散性

新五维超混沌系统(1)满足如下等式

$\nabla V=\frac{\partial \stackrel{\dot{}}{x}}{\partial x}+\frac{\partial \stackrel{\dot{}}{y}}{\partial y}+\frac{\partial \stackrel{\dot{}}{z}}{\partial z}+\frac{\partial \stackrel{\dot{}}{v}}{\partial v}+\frac{\partial \stackrel{\dot{}}{w}}{\partial w}=-\left(a+b-c\right)=-8<0,$

则新五维超混沌系统(1)是耗散的，系统状态的变化是有界的。

2.4. 平衡点分析

令式(1)的右边为0，可得新五维超混沌系统(1)的平衡状态方程为

$\begin{array}{l}a\left(y-x\right)=0,\\ \left(c-a\right)x+cy+w-xz=0,\\ -bz+xy=0,\\ mw=0,\\ -y-hv=0,\end{array}$ (2)

解方程组(2)，令

$\begin{array}{l}{x}_o=y_o=\sqrt{b\left(2c-a\right)},\\ z_o=2c-a,\\ v_o=-\frac{\sqrt{b\left(2c-a\right)}}{h},\end{array}$

可得新五维超混沌系统(1)共有3个平衡点，分别为

$\begin{array}{lll}{S}_1=\left(0,0,0,0,0\right),\hfill & \hfill & S_1=\left(0,0,0,0,0\right),\hfill \\ S_2=\left(x_o,y_o,z_o,v_o,w_o\right),\hfill & \to \hfill & S_2=\left(\sqrt{39},\sqrt{39},13,-\frac{\sqrt{39}}{4},0\right),\hfill \\ S_3=\left(-x_o,-y_o,z_o,-v_o,-w_o\right),\hfill & \hfill & S_3=\left(-\sqrt{39},-\sqrt{39},13,\frac{\sqrt{39}}{4},0\right),\hfill \end{array}$

现以平衡点 $S_1=\left(0,0,0,0,0\right)$ 为例对平衡点处的相关特性进行分析。通过在平衡点 $S_1=\left(0,0,0,0,0\right)$ 处对系统(1)进行线性化，得其Jacobian矩阵为

$J=\left[\begin{array}{ccccc}-a& a& 0& 0& 0\\ c-a& c& 0& 0& 1\\ 0& 0& -b& 0& 0\\ 0& 0& 0& 0& m\\ 0& -1& 0& -h& 0\end{array}\right],$

其特征方程为

$f\left(s\right)=\left(s+b\right)\left[s^4+\left(a-c\right)s^3+\left(a^2-2ac+mh+1\right)s^2+\left(amh+a-cmh\right)s+amh\left(a-2c\right)\right]=0,$

将 $a=23$ ， $b=3$ ， $c=18$ ， $m=12$ ， $h=4$ 代入上式，求得其特征根分别为

$\begin{array}{l}{s}_1=-3.0000,\\ s_2=-19.9753,\\ s_3=14.9115,\\ s_{4,5}=0.0319\pm 6.9414j,\end{array}$

其中， $s_1,s_2<0$ ， $s_3>0$ ， $\mathrm{Re}\left[s_{4,5}\right]>0$ ，有3个位于复平面右半平面的特征根，故平衡点 $S_1=\left(0,0,0,0,0\right)$ 为一不稳定平衡点。其余2个平衡点的分析方法与此处相同，各平衡点的性质分别如表1中所示。

Table 1. Properties of equilibrium points of the novel 5D hyperchaotic system

表1. 新五维超混沌系统各平衡点的性质

2.5. 初值敏感性

将新五维超混沌系统(1)的状态变量的初值分别设定为 $X_{01}=\left(x_0,y_0,z_0,v_{01},w_0\right)=\left(1,1,1,1,1\right)$ 和 $X_{02}=\left(x_0,y_0,z_0,v_{02},w_0\right)=\left(1,1,1,1.00001,1\right)$ ，并保持其他条件均不变，利用Matlab数值仿真软件，绘制出新五维超混沌系统(1)在不同初值下的解曲线，如图1中所示。

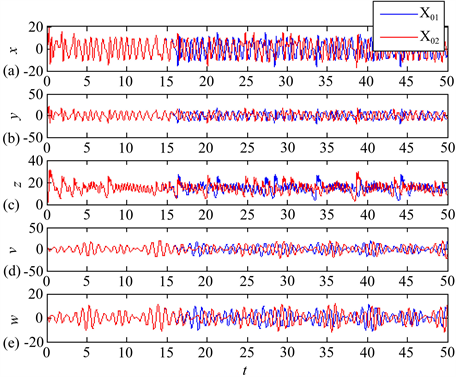
Figure 1. Curves of state variables of the novel 5D hyperchaotic system (1) under different initial values: (a) t-x; (b) t-y; (c) t-z; (d) t-v; (e) t-w

图1. 新五维超混沌系统(1)在不同初值下的解曲线：(a) t-x；(b) t-y；(c) t-z；(d) t-v；(e) t-w

从图1中可以看出，仅仅是将新五维超混沌系统(1)中v的初值变化了0.01‰，其他条件均保持不变，经过很短的一段时间后，系统解曲线的变化明显，说明新五维超混沌系统(1)具有初值敏感性，而初值敏感性同样也是超混沌运动的一个重要特征。

2.6. 新五维超混沌系统的超混沌吸引子

令新五维超混沌系统(1)的初值为 $\left(x_0,y_0,z_0,v_0,w_0\right)=\left(1,1,1,1,1\right)$ ，借由Matlab数值仿真软件，计算出系统的Lyapunov指数分别为

$\begin{array}{l}{\lambda }_1=0.8732>0,\\ {\lambda }_2=0.1282>0,\\ {\lambda }_3=-0.0013\approx 0,\\ {\lambda }_4=-0.5770<0,\\ {\lambda }_5=-8.4231<0,\end{array}$

系统有两个正的Lyapunov指数、一个等于零的Lyapunov指数和两个负的Lyapunov指数，说明此时新五维超混沌系统(1)可产生超混沌运动。由此可计算出新五维超混沌系统(1)的Lyapunov维数 $d_L$ 为

$d_L=j+\frac{{\displaystyle \underset{i=1}{\overset{j}{\sum }}{\lambda }_i}}{\left|{\lambda }_{j+1}\right|}=4+\frac{0.8732+0.1282+\left(-0.0013\right)+\left(-0.5770\right)}{8.4231}=4.0502,$ (3)

其中， $j$ 是使 ${\displaystyle \underset{i=1}{\overset{j}{\sum }}{\lambda }_i}>0$ 的最大整数 [11] 。由式(3)可知，新五维超混沌系统(1)的维数是三维以上的分维数。利用Matlab数值仿真软件，绘制出新五维超混沌系统(1)各相轨迹的曲线，如图2中(a1)~(a10)中所示。

Figure 2. Numerical simulation phase portraits of the novel 5D hyperchaotic system (1): (a1) x-y; (a2) x-z; (a3) x-v; (a4) x-w; (a5) y-z; (a6) y-v; (a7) y-w; (a8) z-v; (a9) z-w; (a10) v-w

图2. 新五维超混沌系统(1)的数值仿真相轨迹曲线：(a1) x-y；(a2) x-z；(a3) x-v；(a4) x-w；(a5) y-z；(a6) y-v；(a7) y-w；(a8) z-v；(a9) z-w；(a10) v-w

2.7. 小结

由上述分析可知，由于新五维超混沌系统(1)具有耗散性，因此，做超混沌运动的新五维超混沌系统(1)从整体来说是稳定的，吸引子外的一切轨线都要收缩进入到吸引子中。但就局部而言，由于新五维超混沌系统(1)的3个平衡点均是不稳定的平衡点，吸引子内的运动又是不稳定的，相邻轨道要相互排斥而按指数形式分离，从而不具有轨道稳定性且具有初值敏感性。所以，新五维超混沌系统(1)的超混沌吸引子是整体稳定性和局部不稳定性的矛盾结合体 [11] ，这使得系统的超混沌运动既不同于系统渐近稳定时收敛于某一平衡点，也不同于系统不稳定时的发散运动，而兼具有界性、初值敏感性、自相似性、分数维和遍历性，因此，超混沌吸引子具有复杂结构。

3. 新五维超混沌系统的电路设计

3.1. 电路设计

现采用超混沌电路改进型模块化设计方法设计新五维超混沌系统(1)的模拟电路模型，主要过程包括变量比例压缩变换、时间尺度变换、标准形式变换、电路模型设计、元件参数确定五个步骤 [12] 。

3.1.1. 变量比例压缩变换

考虑到本文中所采用的模拟元器件的供电电压值均为 $\pm 15\text{V}$ ，通过观察图1和图2可知，状态变量x、y、z、v、w的变化范围均大于模拟元器件允许的饱和电压值，若直接接入电路中，会出现失真现象，故需进行变量比例压缩变换。令 $x=5\tilde{x}$ ， $y=5\tilde{y}$ ， $z=5\tilde{z}$ ， $v=5\tilde{v}$ ， $w=5\tilde{w}$ ，并代入式(1)，可得

$\begin{array}{l}\frac{\text{d}\tilde{x}}{\text{d}t}=a\left(\tilde{y}-\tilde{x}\right),\\ \frac{\text{d}\tilde{y}}{\text{d}t}=\left(c-a\right)\tilde{x}+c\tilde{y}+\tilde{w}-5\tilde{x}\tilde{z},\\ \frac{\text{d}\tilde{z}}{\text{d}t}=-b\tilde{z}+5\tilde{x}\tilde{y},\\ \frac{\text{d}\tilde{v}}{\text{d}t}=m\tilde{w},\\ \frac{\text{d}\tilde{w}}{\text{d}t}=-\tilde{y}-h\tilde{v}.\end{array}$ (4)

3.1.2. 时间尺度变换

为便于在模拟电路模型的输出信号中观察到超混沌运动现象，需对系统(4)进行时间尺度变换，令 $t={\tau }_0{t}_1$ ，则

$\begin{array}{l}\frac{\text{d}\tilde{x}}{\text{d}{t}_1}=a{\tau }_0\left(\tilde{y}-\tilde{x}\right),\\ \frac{\text{d}\tilde{y}}{\text{d}{t}_1}=\left(c-a\right){\tau }_0\tilde{x}+c{\tau }_0\tilde{y}+{\tau }_0\tilde{w}-5{\tau }_0\tilde{x}\tilde{z},\\ \frac{\text{d}\tilde{z}}{\text{d}{t}_1}=-b{\tau }_0\tilde{z}+5{\tau }_0\tilde{x}\tilde{y},\\ \frac{\text{d}\tilde{v}}{\text{d}{t}_1}=m{\tau }_0\tilde{w},\\ \frac{\text{d}\tilde{w}}{\text{d}{t}_1}=-{\tau }_0\tilde{y}-h{\tau }_0\tilde{v},\end{array}$ (5)

其中， ${\tau }_0=100$ 。

3.1.3. 标准形式变换

由于模拟电路模型中的运算放大器均采用反相输入方式，为便于模拟电路模型的搭建，需将系统(5)变换为标准形式，即

$\begin{array}{l}\frac{\text{d}\tilde{x}}{\text{d}{t}_1}=-a{\tau }_0\tilde{x}-a{\tau }_0\left(-\tilde{y}\right),\\ \frac{\text{d}\tilde{y}}{\text{d}{t}_1}=-\left(a-c\right){\tau }_0\tilde{x}-c{\tau }_0\left(-\tilde{y}\right)-{\tau }_0\left(-\tilde{w}\right)-5{\tau }_0\tilde{x}\tilde{z},\\ \frac{\text{d}\tilde{z}}{\text{d}{t}_1}=-b{\tau }_0\tilde{z}-5{\tau }_0\tilde{x}\left(-\tilde{y}\right),\\ \frac{\text{d}\tilde{v}}{\text{d}{t}_1}=-m{\tau }_0\left(-\tilde{w}\right),\\ \frac{\text{d}\tilde{w}}{\text{d}{t}_1}=-{\tau }_0\tilde{y}-h{\tau }_0\tilde{v}.\end{array}$ (6)

3.1.4. 电路模型设计

由式(6)设计相应的改进型模块电路并将输入、输出项对应连接，可得系统(6)的模拟电路模型，如图3中所示。本文中所采用的运算放大器的型号均为TL082CP，乘法器的型号均为AD734AN。

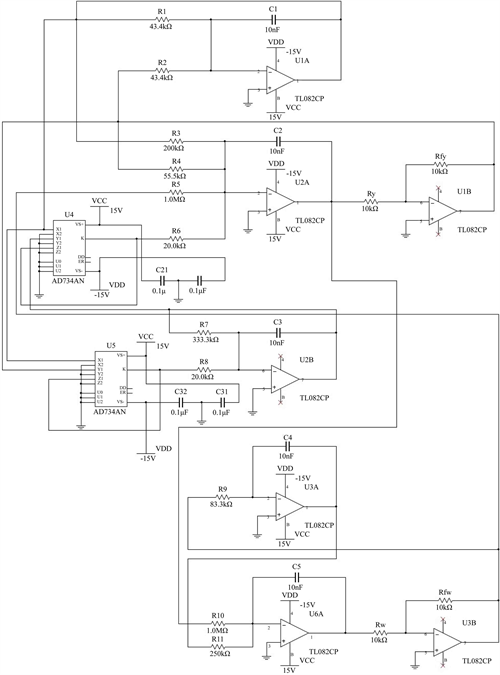
Figure 3. Analog circuit model of the system (6)

图3. 系统(6)的模拟电路模型

3.1.5. 元件参数确定

由图3，可得该模拟电路模型的状态方程为

$\begin{array}{l}\frac{\text{d}\tilde{x}}{\text{d}{t}_1}=-\frac{1}{{\text{R}}_1{\text{C}}_1}\tilde{x}-\frac{1}{{\text{R}}_2{\text{C}}_1}\left(-\tilde{y}\right),\\ \frac{\text{d}\tilde{y}}{\text{d}{t}_1}=-\frac{1}{{\text{R}}_3{\text{C}}_2}\tilde{x}-\frac{1}{{\text{R}}_4{\text{C}}_2}\left(-\tilde{y}\right)-\frac{1}{{\text{R}}_5{\text{C}}_2}\left(-\tilde{w}\right)-\frac{1}{{\text{10R}}_6{\text{C}}_2}\tilde{x}\tilde{z},\\ \frac{\text{d}\tilde{z}}{\text{d}{t}_1}=-\frac{1}{{\text{R}}_7{\text{C}}_3}\tilde{z}-\frac{1}{{\text{10R}}_8{\text{C}}_3}\tilde{x}\left(-\tilde{y}\right),\\ \frac{\text{d}\tilde{v}}{\text{d}{t}_1}=-\frac{1}{{\text{R}}_9{\text{C}}_4}\left(-\tilde{w}\right),\\ \frac{\text{d}\tilde{w}}{\text{d}{t}_1}=-\frac{1}{{\text{R}}_{10}{\text{C}}_5}\tilde{y}-\frac{1}{{\text{R}}_{11}{\text{C}}_5}\tilde{v}.\end{array}$ (7)

令式(7)与式(6)中对应项系数相等，已知 ${\text{C}}_1={\text{C}}_2={\text{C}}_3={\text{C}}_4={\text{C}}_5=\text{10}\text{nF,}$ ， ${\text{R}}_{\text{y}}={\text{R}}_{\text{fy}}={\text{R}}_{\text{w}}={\text{R}}_{\text{fw}}=10\text{kΩ}$ ，则

$\begin{array}{l}\frac{1}{{\text{R}}_1{\text{C}}_1}=\frac{1}{{\text{R}}_2{\text{C}}_1}=a{\tau }_0\to {\text{R}}_1={\text{R}}_2=\frac{1}{a{\tau }_0{\text{C}}_1}\approx 43.4\text{kΩ},\\ \frac{1}{{\text{R}}_3{\text{C}}_2}=\left(a-c\right){\tau }_0\to {\text{R}}_3=\frac{1}{\left(a-c\right){\tau }_0{\text{C}}_2}=200\text{kΩ},\\ \frac{1}{{\text{R}}_4{\text{C}}_2}=c{\tau }_0\to {\text{R}}_4=\frac{1}{c{\tau }_0{\text{C}}_2}\approx 55.5\text{kΩ},\\ \frac{1}{{\text{R}}_5{\text{C}}_2}=\frac{1}{{\text{R}}_{10}{\text{C}}_5}={\tau }_0\to {\text{R}}_5={\text{R}}_{10}=\frac{1}{{\tau }_0{\text{C}}_2}=1\text{MΩ},\\ \frac{1}{{\text{10R}}_6{\text{C}}_2}=\frac{1}{{\text{10R}}_8{\text{C}}_3}=5{\tau }_0\to {\text{R}}_6={\text{R}}_8=\frac{1}{50{\tau }_0{\text{C}}_2}=20\text{kΩ}\end{array}$

$\begin{array}{l}\frac{1}{{\text{R}}_7{\text{C}}_3}=b{\tau }_0\to {\text{R}}_7=\frac{1}{b{\tau }_0{\text{C}}_3}\approx 333.3\text{kΩ},\\ \frac{1}{{\text{R}}_9{\text{C}}_4}=m{\tau }_0\to {\text{R}}_9=\frac{1}{m{\tau }_0{\text{C}}_4}\approx 83.3\text{kΩ},\\ \frac{1}{{\text{R}}_{11}{\text{C}}_5}=h{\tau }_0\to {\text{R}}_{11}=\frac{1}{h{\tau }_0{\text{C}}_5}=250\text{kΩ}.\end{array}$

3.2. 电路仿真

应用Multisim电路仿真软件搭建如图3中所示的新五维超混沌系统的模拟电路模型。通过电路仿真得到的相轨迹曲线如图4中(b1)~(b10)中所示。图中x、z、w的示波器显示刻度为1V/Div，y、v的示波器显示刻度为2V/Div。

逐一对比图4中(b1)~(b10)与图2中(a1)~(a10)，考虑到在元件参数确定过程中存在元件参数的近似计算，使得模拟电路模型与如式(6)所示的精确数学模型在参数上存在误差；同时，由于受到模拟电路模型中乘法器模块的非线性特性、元器件精度以及仿真软件性能的影响，使得如图4中所示的模拟电路模型的电路仿真相轨迹曲线与如图2中所示的精确数学模型的数值仿真相轨迹曲线在曲线形状、状态变量变化范围上均存在一定差异。但从定性分析的角度出发，仍可认为如图4中所示的电路仿真曲线与如图2中所示的数值仿真曲线相一致，并基于此认为所设计的模拟电路模型是正确的。

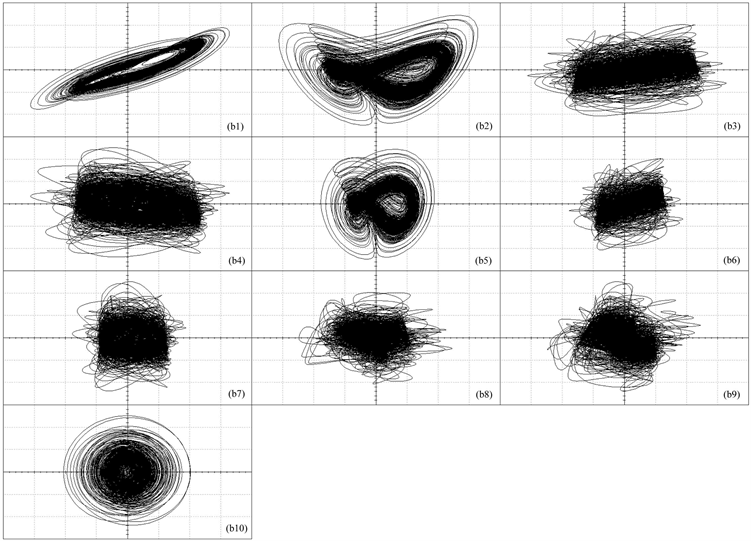
Figure 4. Circuit simulation phase portraits of the novel 5D hyperchaotic system: (b1) x-y; (b2) x-z; (b3) x-v; (b4) x-w; (b5) y-z; (b6) y-v; (b7) y-w; (b8) z-v; (b9) z-w; (b10) v-w

图4. 新五维超混沌系统的电路仿真相轨迹曲线：(b1) x-y；(b2) x-z；(b3) x-v；(b4) x-w；(b5) y-z；(b6) y-v；(b7) y-w；(b8) z-v；(b9) z-w；(b10) v-w

4. 结论

本文通过分析新五维超混沌系统的对称性、耗散性、平衡点特性、初值敏感性和超混沌吸引子特性，从理论上证明了新五维超混沌系统中超混沌运动现象的存在性。在此基础上，采用超混沌电路改进型模块化设计方法设计出新五维超混沌系统的模拟电路模型。通过逐一对比由Multisim电路仿真软件绘制的电路仿真相轨迹曲线和由Matlab数值仿真软件绘制的数值仿真相轨迹曲线，定性地验证了所设计的新五维超混沌系统的模拟电路模型的正确性。下一步，拟完成本文所设计的新五维超混沌系统的模拟电路模型的硬件实现。由于本文所设计的新五维超混沌系统维数高，其产生的超混沌运动较之混沌运动更为复杂，因此，更适合应用于超混沌控制、超混沌同步、保密通信等的研究中。