1. 引言
“传热学”是研究由温差引起的热能传递规律的科学,热辐射是“传热学”课程中最基本、最复杂的一种传热方式 [1] 。只要当物体的温度大于0 K,物体就会发出热辐射,因此它也是一种处处存在的传热方式。由于热辐射的复杂性,人们从19世纪才开始对这种传热方式进行研究,而在“传热学”授课过程中,学生对于热辐射的理解往往比较浅显,仅仅依靠课堂教学很难使学生正确理解基本规律和公式 [2] [3] [4] 。为此,笔者在授课过程中有意扩展这方面的讲解和实践,试图加强学生对热辐射的理解和认识。
本文笔者以“传热学”中与热辐射相关的黑体辐射五大定律为例介绍实际教学中的探索和实践。一般教材中直接给出黑体辐射基本定律的表达式,而由于教学课时的限制,授课教师也很少对其做过多的阐述,因此学生很难做到真正理解、吃透和掌握。笔者在授课过程中,先基于MATLAB做出它们的图像,从图形上说明普朗克定律与各公式、定律的联系;再由数学分析理论从普朗克定律导出其他公式、定律,进一步讨论它们之间的关系。这样数形结合的分析和讨论,既能增强学生对这些枯燥无味公式的记忆,又能加深学生的理解。
2. 黑体辐射五大定律图形关系
普朗克定律为普朗克于1900年从理论上推导确定,是热辐射最基本的定律,它反应了光谱辐射力
和波长
、温度T之间的关系,即
(1)
其中
、
分别为第一辐射常数、第二辐射常数。由于普朗克定律的重要性,笔者在授课过程均是围绕它进行展开。需要指出的是,研究表明,基于普朗克公式计算的结果与黑体辐射实验结果吻合非常好。
2.1. 普朗克定律、维恩公式和瑞利–金斯公式间的图形关系
在普朗克公式提出之前,笔者从物理学史出发,先介绍了维恩公式(1893年,维恩推导得到)和瑞利–金斯公式(1900年,瑞利从经典统计力学进行了推导;1905年,金斯进行了修正),然后才引入普朗克公式。维恩公式、瑞利–金斯公式分别为
(2)
(3)
其中
为第三辐射常数。
对于维恩公式和瑞利–金斯公式,“传热学”书上一般不作介绍,为了让学生全面理解普朗克定律,根据三个公式,笔者利用Matlab软件 [5] 通过图形形象展示了他们之间的关系,程序代码及温度为1000 K时的分布如图1所示。由图可清晰看出三者间的关系:在短波处,维恩公式与普朗克定律吻合很好,但长波处有些偏差;而瑞利–金斯公式在长波处与普朗克公式吻合较好,但在短波出趋于无穷大,也就是所谓的“紫外灾难”。
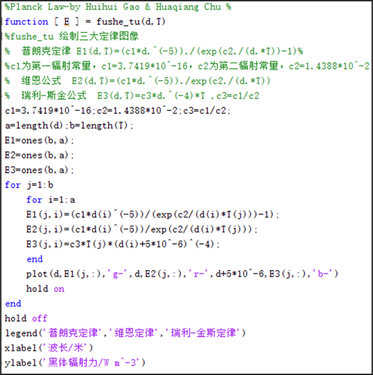 (a)
(a)  (b)
(b)
Figure 1. Matlab code and the relationship between the three laws
图1. Matlab代码及三个定律间的关系
2.2. 普朗克定律、维恩位移定律和斯忒藩-玻尔兹曼定律间的图形关系
维恩位移定律和斯忒藩–玻尔兹曼定律是“传热学”中另外两个重要的黑体辐射定律。维恩位移定律表述的是黑体辐射的光谱辐射力最大处的波长与温度之间的关系,即
(4)
图2给出了普朗克定律、维恩位移定律两个公式的计算程序代码及图形关系。图中的曲线为光谱辐射力随温度、波长的变化分布,最高点为光谱辐射力最大处,这样可很清楚地看出二者之间的关系。
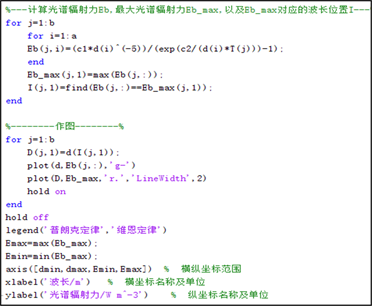 (a)
(a)  (b)
(b)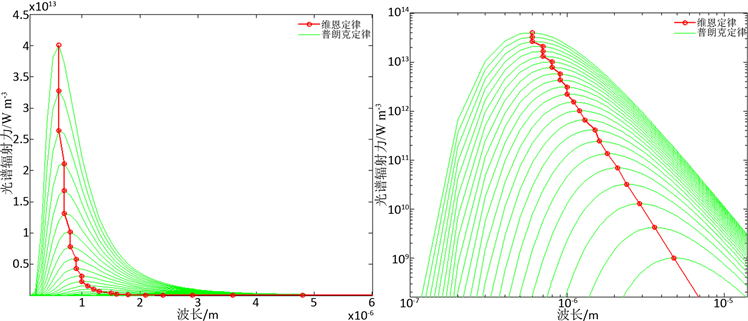 (c) (d)
(c) (d)
Figure 2. Matlab code and Graphic Relations between Planck’s Law and Venn’s law of displacement ((c), (d))
图2. 普朗克定律、维恩位移定律Matlab代码及图形关系(图(c)为算术坐标,图(d)为对数坐标)
斯忒藩–玻尔兹曼定律则描述了黑体辐射力与温度之间的关系,即
(5)
根据定义可知,该公式是普朗克定律(公式(1))在同温度下关于所有波长范围内的积分,即普朗克曲线的阴影面积,如图3所示,这一点在后面的公式推导过程会更清晰地展现。
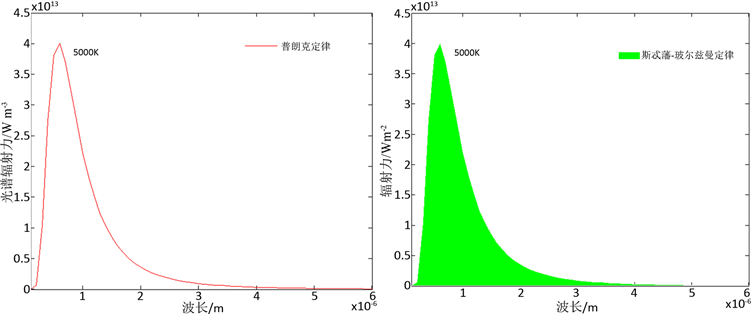 (a) (b)
(a) (b)
Figure 3. Graphic Relations between Planck's Law and Stefan-Boltzmann’s Law
图3. 普朗克定律、斯忒藩-玻尔兹曼定律图形关系
通过这样图形的演示,直观形象地展示传热规律,让学生对五大定律有了一个形象的认识,增强学生学习的兴趣与动力,加强学生对传热基本概念、规律的理解和掌握。
3. 黑体辐射五大定律公式推导
虽然学生形象认识了五大定律,但不足以掌握他们之间的规律,为此,笔者在授课过程中,先给出了五大定律的公式,然后让学生试着推导他们的转换,从而让他们理解五大定律中每一个参数的物理意义。
3.1. 普朗克定律、维恩公式和瑞利–金斯公式间的关系推导
根据普朗克定律、维恩公式和瑞利–金斯公式的形式和图1(b),可以发现,当
,即
时,普朗克定律可近似为维恩公式:
。因此,在温度一定时,当波长比较短的情况下,普朗克定律可近似为维恩公式;在工程中,当温度较高时,人们可采用维恩公式代替普朗克定律。
当
,即当
时,对
在
处进行泰勒展开有,
,忽略二阶项后将此式代入普朗克定律即可得瑞利–金斯公式:
。因此,在温度一定时,波长比较长情况下普朗克定律可近似为瑞利–金斯公式。
3.2. 普朗克定律、维恩位移定律和斯忒藩–玻尔兹曼定律间公式推导
由图1(b)我们知道,光谱辐射力随波长连续变化,并且在一定温度下的曲线有一个极大值,而维恩位移定律中波长为普朗克定律中最大光谱辐射力对应的波长,所以找到最大光谱辐射力就找到了其对应的波长。根据数学知识,普朗克定律对波长求一阶偏导并令其等于0即可得到峰值波长与温度的关系,即维恩位移定律,具体推导过程如图4所示。
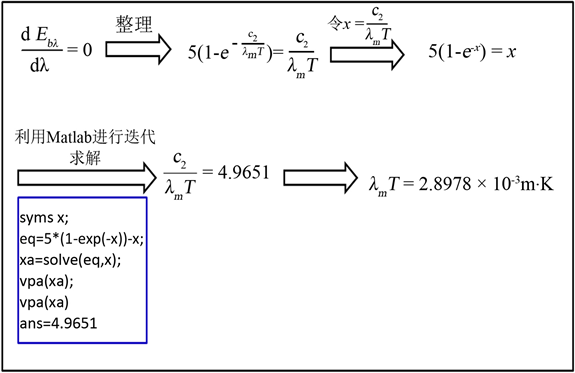
Figure 4. Derived relations between Planck’s law and Wien’s law
图4. 普朗克定律与维恩位移定律间推导关系
根据黑体光谱辐射力和辐射力定义可,要求黑体辐射力只需普朗克定律对波长积分即可,具体推导过程如图5所示。
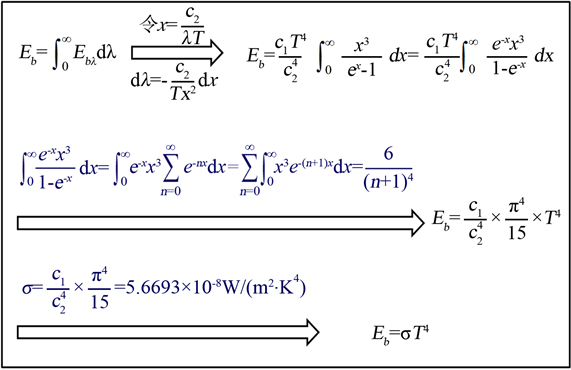
Figure 5. Derived relations between Planck’s Law and Stefan-Boltzmann’s Law
图5. 普朗克定律与斯忒藩-玻尔兹曼定律间推导关系
根据图5可知,经过这样一个积分,从普朗克定律出发可得到斯忒藩-玻尔兹曼,虽然后者比前者早。总之,经过这样的一系列的公式推导,使得学生掌握了五大定律间的脉络变化和相互关系,如图6所示,同时通过这样理论推导,可使学生更容易理解图1、图2和图3中的结果,并且可从本质上“吃透”普朗克定律。

Figure 6. Correlation between five laws of blackbody radiation
图6. 黑体辐射五大定律相互关系
4. 结束语
通过对普朗克定律与其他公式数学分析、讨论和图像可视化展示相结合的方式,既增强了学生对这些枯燥无味公式的记忆,又能加深学生对这些基本定律的理解,同时为学习黑体辐射理论知识增添了一定的趣味性,进而有望提高学生学习的积极性和主动性。
基金项目
本文得到安徽工业大学教改课题(2016jy39, 2015006);高等学校能源动力类专业教育学改革项目(NDJZW2016Y-1, NDXGK2017Y-30);安徽省高等学校省级精品开放课程(2012gkk022);教育部卓越工程师教育培养计划的支持。
致谢
感谢安徽工业大学能源与动力工程专业2014级卓越工程师班所有同学!