1. 引言
应变计是应变式传感器制造的核心敏感元件,也是结构强度测试、应力分析等应用的主要测量传感器 [1] ,广泛应用于航空航天、计量测试、交通运输等领域。应变式传感器的弹性体结构尺寸设计依赖于额定输出、应变计灵敏系数和材料弹性模量。
应变计的特性参数是随温度变化的,由于环境的影响,应变计的指示应变与实际相差甚远,甚至不能确定指示应变曲线的真实性 [2] 。灵敏系数是表征应变计的电阻变化与应变变形之间的关系,这一应变计特性参数的准确性,会对真实应变修正带来影响,甚至引入较大的误差。究其原因,是应变计的标定参数问题尚未完全解决,灵敏系数标定的影响因素未能明确,从而影响到应变测试的精度 [3] [4] 。
本文利用砝码加载的四点式弯矩简支梁检定装置和SK-1钢架梁结构装置,分别从原理和实际测试数据对比方面对灵敏系数标定误差影响因素进行分析,对参数标定和温度下测试具有重要的参考意义。
2. 应变计工作原理
普通电阻应变计采用金属箔栅作为测量体,高分子材料作为基底传递应变。在实际测量时,结构试件发生变形,应变计跟随变形,构件表面应变通过基底和贴片胶剪切传递到敏感栅上,应变计产生电阻变化,根据欧姆定律应变计的电阻:
(1)
式中R为应变计敏感栅的电阻;ρ为应变计敏感栅的电阻率;n为敏感栅的栅根数;L为单根敏感栅长度;S为单根敏感栅截面积。
当应变计跟随试件的应变ε变形时,应变计的敏感栅电阻也发生变化,即对式(1)全微分:
(2)
其中:
(3)
从而得出应变与电阻变化之间的关系,即灵敏系数:
(4)
只需要测量应变计的电阻变化,就可以得到结构试件的变形。应变仪的指示应变通过灵敏系数修正得到真实机械变形应变。应变计的灵敏系数真实性和准确性对采用应变计的应变测量而言十分重要 [2] [5] 。
3. 应变计灵敏系数测量模型原理
应变计灵敏系数标定常用的标准机械载荷变形试验用原理模型有砝码加载四点式简支梁结构原理和钢架纯弯梁结构,分别对其原理模型和计算进行分析。
3.1. 砝码加载四点式简支梁结构
砝码加载的四点式简支梁采用两端支点支撑,中间两点加载 [4] ,中心点采用百分表或挠度计测量位移挠度,其受力简图见图1。
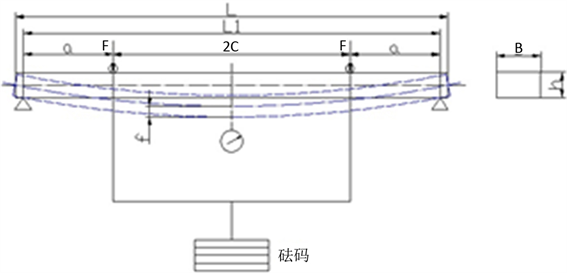
Figure 1. Curve: system result of standard experiment Schematic diagram of loading model of simple supported beam with weight loading
图1. 砝码加载四点式简支梁加载模型示意图
砝码加载的四点式简支梁采用两端支点支撑,中间两点加载 [4] ,中心点采用百分表或挠度计测量位移挠度,其受力简图见图1。
(5)
根据胡克定律得:
(6)
式中ε为试验梁理论应变量;δ为试验梁弯曲应力;E为试验梁弹性模量;W为试验梁抗弯截面系数,试验梁为矩形截面,W = Bh2/6。
根据材料力学挠度曲线公式,弯矩梁中心位置挠度为:
(7)
由式(6)、式(7)可得应变与挠度的近似关系:
(8)
式中h为试验梁的厚度;f为试验梁中间点的挠度值;L1为试验梁有效长度(即两支点之间距离)。
由式(8)得知,试验梁表面应变与试验梁尺寸、加载点位置、支点之间的试验梁有效长度、挠度值有关。砝码加载无法做到挠度控制加载,挠度还与弹性模量、砝码重量有关。
3.2. 纯弯矩钢架梁结构
纯弯矩钢架梁采用两端刚刚度力臂开合带动试验梁弯曲变形,中心点采用高精度三点挠度计测量位移挠度,控制力臂开合度,以保证试验梁中心点挠度达到准确值 [4] [5] 。其受力简图见图2。

Figure 2. Diagram of forces on pure moment steel frame beam
图2. 纯弯矩钢架梁受力示意图
根据图2,刚性力臂端头施加δ力值(δ+, δ−),试验梁两端的弯矩属于纯弯矩,梁上任一点的弯矩为:
(9)
与简支梁一致,根据胡克定律,可得纯弯矩梁表面的应变大小为:
(10)
ε±为试验梁理论应变;σ为试验梁弯曲应力;E为试验梁弹性模量;W为试验梁抗弯截面系数,试验梁为矩形截面,W = Bh2/6。在实际状况下,试验梁还受一对非常小的轴向力,试验梁表面的凹、凸真实应变为:
凹面
(11)
凸面
(12)
根据三点式挠度法测得的纯弯梁凹、凸变形精确应变与试验梁中心位置的挠度f之间的关系为:
(13)
 (14)
(14)
式中h为试验梁的厚度;f为试验梁中间点的挠度值;a为力臂长度;c为三点挠度计安装支点距离的一半;μ为试验梁的泊松系数。
采用三点挠度计挠度值控制试验梁的加载,试验梁的表面挠度只与试验梁的厚度、三点挠度计安装支点的距离、泊松系数和应变量有关。
4. 不同测量方式对灵敏系数标定的影响因素分析和验证
应变计灵敏系数标定常用的标准机械载荷变形试验用原理模型有砝码加载四点式简支梁结构原理和钢架纯弯梁结构,分别对其原理模型和计算进行分析。
4.1.常温灵敏系数测试
通过前面的分析,应变计的灵敏系数为
(15)
在实际测试中,应变仪上设定的灵敏系数为2,那应变计实际的灵敏系数K为:
(16)
式中εs为应变仪测量的指示应变;εj为试验梁加载的标准机械应变,一般为1000 μm/m。
4.1.1. 试验梁影响误差
试验梁截面是矩形,理论上受纯弯矩量表面变形形成圆柱体面,得到均匀的等应变场。梁的横截面形状对梁表面应变均匀性会有影响,影响误差为:
(17)
式中s = B/h,梁宽和梁厚之比;μ为试验梁泊松比;ε为标准载荷应变,一般为1000 μm/m。
对于四点简支梁,试验梁宽度B = 30 mm,试验梁厚度h = 6 mm,s = 30/6 = 5,试验梁泊松比μ = 0.3,则
(18)
对于钢架梁,试验梁宽度B为25.5 mm,试验梁厚度h = 25.5 mm,s = 25.5/25.5 = 1,试验梁泊松比μ = 0.3,则
(19)
从结果过来看,钢架梁应变误差只有四点简支梁的一半不到。四点简支梁属于薄矩形梁,宽厚差异较大,要保证均匀性难度较大,会进一步影响试验梁的应变,梁越薄误差越大。钢架梁属于矩形梁,宽度厚度一致,梁的均匀性易保证,加工难度低。
4.1.2. 不同标定装置测试常温灵敏系数误差验证
试验梁均采用40CrMoNiA合金钢材料,弹性模量为209 GPa,泊松系数μ为0.3,线膨胀系数11.3 × 10−6/℃。四点式简支梁装置的试验梁尺寸为420 × 30 × 6 mm3,SK-1钢架梁装置的尺寸为780 × 25.076 × 25.076 mm3,使用同一批ZEMIC的BYM350-3AA(23)T0-C薄膜应变计,采用H-600胶贴片 [6] 进行对比测试,结果如表1。

Table 1. List of room temperature gage factor calibrated by different devices
表1. 不同装置标定的常温灵敏系数列表
从数据来看,砝码加载的简支梁灵敏系数比钢架梁大约0.7%,分散明显偏大。
4.2. 温度下灵敏系数测试
4.2.1. 温度下试验梁载荷应变对灵敏系数测试的影响
砝码加载的四点式简支梁在温度下对灵敏系数测试时,试验梁的应变与弹性模量E和尺寸变化相关。根据简支梁力学模型
(20)
试验梁形状和弹性模量引起的误差相当于对式(25)进行全微分。
(21)
式中a为砝码加载点与支点之间最近距离;B试验梁宽度;h为试验梁厚度;E为试验梁弹性模量;G为砝码重量;Va为温度下砝码加载点和支点之间距离变化量;VB为温度下试验梁宽度的变化量;Vh为温度下试验梁厚度的变化量;VE试验梁弹性模量温度下的变化量;VG砝码的变化。

Table 2. List of linear expansion coefficient of 40CrMoNiA alloy steel test beam
表2. 40CrMoNiA合金钢试验梁线膨胀系数列表

Table 3. List of elastic modulus of 40CrMoNiA alloy steel test beam
表3. 40CrMoNiA合金钢试验梁弹性模量列表
当温度200℃时,通过查表2、表3可知,试验梁的线膨胀系数从11.3 × 10−6/℃变化到11.9 × 10−6/℃,变化0.6 × 10−6/℃;弹性模量从209 GPa变化到203 GPa,变化量为−6 GPa;泊松比μ = 0.3;砝码在外部加载,试验梁受温度影响自由膨胀,可不考虑加载点的位置变化带来载荷影响。因此其综合误差为:
最大的误差源是弹性模量的变化引起,占总误差的99%以上。
如果砝码为150 kg,常温下对四点简支梁加载,梁表面应变量为:
(27)
高温200℃时,试验梁加载点与支点间距a从5 cm变化为
;梁厚h从0.6 cm变化为
,梁宽B从3 cm变化为梁表面的应变量为
;梁的弹性模量为203 GPa,则200℃下砝码加载的应变量为:
(28)
机械载荷应变量就会增加39 μm/m,如果还是按照标准997 μm/m计算,明显计算后的200℃灵敏系数就会偏大一些,但如果按照1036 μm/m计算,可能和实际又会有差异。
对于钢架梁结构,其应变量与挠度、三点挠度计刀口间距、试验梁厚度和力臂长度有关,但力臂在温箱外部,力臂无变化,主要是刀口间距c、梁厚h温度下尺寸变化的影响,误差计算结果为
钢架梁试验梁采用标准1000 μm/m和挠度值f相适应来控制,因此载荷应变量基本恒定。凸面挠度与应变关系计算式为:
(29)
其中
式中ε+试验梁标准机械应变;c为挠度计刀口距离的一半;h为试验梁厚度;a为力臂长度。
从上式(29)可以看到,误差0.0012%,远远小于四点式简支梁结构。
如果挠度不变,仅考虑梁尺寸变化,那么试验梁常温下表面应变为:
高温200℃时,试验梁厚度变化
;挠度计刀口变化
;a和f不变,高温200℃试验梁表面机械应变为:
如果挠度f不变,200℃下机械应变减少8.7 μm/m,误差约为0.87%,远小于简支梁结构。
4.2.2. 温度下不同试验梁结构标定灵敏系数随温度变化实际数据
根据前述分析,采用中温应变计ZAB350-3AA250(23)N2-C和F-614贴片胶粘贴,试验梁采用40CrMoNiA合金钢,分别采用四点式简支梁结构和纯弯矩钢架梁结构按照国标 [6] 测试灵敏系数随温度变化,具体数据见表4和曲线示意图见图3。

Table 4. Test data sheet of gage factor with temperature change by simply supported beam and steel frame beam structure
表4. 简支梁结构和钢架梁结构灵敏系数随温度变化测试数据表
通过数据和曲线分析,四点简支梁数据相对SK-1钢架梁偏大,存在非线性,主要是试验梁弹性模量、线涨系数发生变化导致。基本趋势与钢架梁接近,与卡玛应变计的理论趋势一致。相对而言,钢架梁结构测量误差最小,也最接近于真实数据。
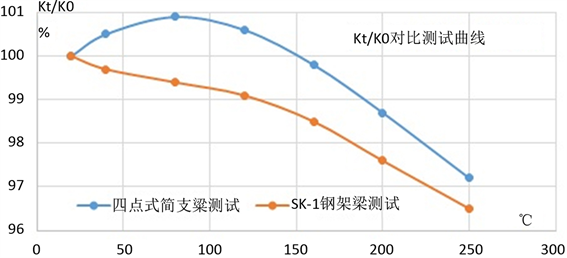
Figure 3. Curve of the gage factor of with temperature by different testing mechanism varies
图3. 不同测试机构灵敏系数随温度变化测试曲线图
5. 结论
通过理论分析和实际测试,确定了应变计灵敏系数标定中的主要误差源,对误差源进行了分析。对比了砝码加载四点式简支梁结构和纯弯矩钢架梁结构在常温灵敏系数、温度下灵敏系数随温度变化的误差源大小,分析出各自的优势和缺点,明确钢架梁误差最小,测试结果也得到验证,得出应变计性能的标定优选方案,为传感器设计制造和应变测试提供更准确的参考修正参数。
结果表明,砝码加载简支梁常温下灵敏系数测试数据与钢架梁接近,误差0.3758%,但分散明显高于钢架梁;温度下,简支梁弹性模量、试验梁尺寸变化引起的测量误差达2.9%,灵敏系数随温度变化曲线明显偏离,在实际灵敏系数标定中应予以重视。