1. 引言
语义网旨在构建机器可读的网络,近年来受到越来越多的关注。为了应对具有语义丰富性的各种查询,必须对现实世界的信息和知识进行结构化提取和整合,这仍然是计算机科学中的一个挑战 [1] 。由结构化RDF (Resource Description Framework)数据互联而形成的数据网被公认为是一种实现语义网的重要途径 [2] 。近年来,可用的结构化RDF数据增加了几个数量级 [3] 。根据关联开放数据(LOD)项目显示,截至2018年6月,已有16,136个链接连接着1234个数据集,比如DBpedia,FOAF,MusicBrainz和Geonames,这些数据集被发布和链接,形成了LOD云数据网。向数据网添加地理空间数据集会给其他类型的数据集增添更多的有用信息 [4] ,目前在LOD云中已有多个地理空间RDF数据集,如NationalMap,LinkedGeoData,NUTS和GADM,在地理空间数据集和其他类型的数据集之间建立关联可以为其他类型的数据集提供地理空间背景。
为了使人或机器能够浏览数据网,数据集必须要关联起来 [5] 。RDF关联将数据网中的数据关联起来,消除信息孤岛,使人或机器能够从一个数据集被导航到另一个数据集。RDF关联可以分为三种类型:关系关联,词表关联和同质关联。关系关联链接彼此相关的实体,如书籍及其作者或房屋及其所有者。词表关联将描述数据的词汇术语链接起来。同质关联链接标识同一实体的统一资源标识符(URI)。
同质关联目前有两种实现方法。一种是基于关键字的方法,它适用于具有统一命名规则的情况。例如,在出版领域,每本书都有特定的国际标准书号(ISBN),使书籍之间的关联变得简单。另一种是基于相似性的方法,比较两个实体并量化它们的相似性。如果相似度超过给定阈值,则认为应建立两个实体间的同质关联 [6] 。
在基于相似度的方法中,必须明确如何度量两个实体之间的相似性。现有的相似性度量方法有两种:一是句法相似度,例如字符串相似性,可以通过Jaro-Winkler距离 [7] 计算相似性,二是语义相似度 [8] [9] [10] [11] ,可以由字典或更高层次的本体确定。最简单的匹配方法是使用字符串比较实体的名称 [12] [13] ,这种方法简单直观,但在匹配地理空间实体时,因为名称重复现象在地理空间领域非常普遍,所以简单的名称匹配效果并不是很好。 [14] 提出了一种基于Tversky对比模型 [15] 的方法,通过计算地理空间实体的名称,城市和省份属性的相似性的加权和来确定两个地理空间实体之间的相似性。这种方法在一定程度上解决了名称重复的问题。Pschorr等人 [16] 通过比较经纬度来构建传感器数据和GeoNames数据库之间的关联。Auer等人 [2] 通过计算名称和空间相似度来实现LinkedGeoData和DBpedia之间的匹配,其中,空间相似度由值域在0到1之间的二次函数确定:如果两个点完全相符,那么函数的值将为1,如果两点之间的距离达到预定义的最大距离,函数值为0。但是,每种空间实体的最大距离不是显而易见的,而且要为不同类型的空间实体定义不同的最大距离。Silk [17] 是一个关联探测框架,它提供了Silk-Link规范语言(LSL),允许用户自定义应关联哪些数据集,以及应该使用哪些规则来关联它们。Silk有许多内置的相似度计算方法,如JaroWinklerSimilarity,numSimilarity和taxonomicSimilarity。
因为不同的RDF数据发布者对同一个实体可能会有不同的描述,所以数据网允许发布者使用不同的URI来描述相同的实体,标识同一实体的不同URI称为URI别名。因此,数据网中包含许多不同的URI,却指的是同一个实体。为了消除信息孤岛,构建一个全球的数据网络,这些URI别名通过谓语
[18] 互相关联。这种类型的关联称为同质关联。本文提出了一种基于MapReduce的并行计算方法来构建地理空间实体之间的同质关联。
2. 地理空间实体的同质关联
建立地理空间实体的同质关联首先需要一个可区分的特征来计算地理空间实体之间的相似性。在现实世界中,语言是人类沟通的载体,为了准确地交流沟通,所有的实体都被赋予了一个名称,在虚拟世界中,实体的标识符应该更精确、唯一和明确,以实现机器之间的通信。例如,存储在计算机中的文件由整数唯一标识;在出版领域,图书用ISBN唯一标识。然而,目前国际上没有公认的唯一标识地理空间实体的标准,名称重复现象在地理空间领域是非常普遍的。据初步统计,美国以Madison命名的有28个城市,以Clinton命名的有25个城市,23个Washington,16个Lincoln,17个Jackson。另外,作为一个移民国家,许多市县都是以Denmark,Sweden,Peru,England,Sydney等国家或地区名命名。除了名称重复现象之外,一些数据集提供了不同语言的地理空间实体名称。例如,NUTS是一个为欧盟提供地理信息的数据集,它为地理空间实体提供了不同语言的名称,如德国的名称属性有Deutschland (德语中的德国)和Germany (英语中的德国),意大利的名称属性有Italia (意大利语中的意大利)和Italy (英语中的意大利)。如图1所示,地理空间数据集A和B都有四个实体:A中的Italia和B中的Italy描述同一个地理空间实体,A中的Deutschland和B中的Germany描述同一个地理空间实体,由于地名重复,B中,有两个Madison,如若只匹配地理空间实体的名称,A中Madison将和B中两个Madison都关联起来,而事实是B中只有一个Madison与A中的Madison对应,因此仅仅匹配地理空间实体的名称不是一个完备的策略。在地理空间实体的所有属性中,几何属性(包括位置和形状)对于每个实体来说是唯一的。因此,用这些实体的几何属性来匹配它们是一个较好的策略。本文采用Hausdorff距离计算实体之间的几何属性相似度来量化实体之间的相似度。
一些特定类型的地理空间实体,如城市,州和国家,在地理空间数据库中被抽象为多边形,每个多边形由大量的边界点来描述。包含大量边界点的Hausdorff距离的计算是复杂且耗时的。MapReduce框架是一种用于处理大型数据集的并行计算模型,有望加快匹配过程。为了减少匹配过程的运行时间,提高效率,本文提出了一种基于MapReduce框架的同质关联方法。

Figure 1. Finding matches between geospatial datasets A and B
图1. 关联地理空间数据集A和B
3. 方法
如上所述,对于地理空间实体,属性数据如名称不是唯一的,而提供位置信息和形状信息的几何数据是唯一的。因此,本文通过Hausdorff距离计算两个地理空间实体之间的空间相似性,通过匹配实体的几何数据构建地理空间实体之间的同质关联,与属性数据相比,几何数据具有大数据的特征,匹配过程十分耗时。因此,为了提高效率,本文提出了基于MapReduce的并行框架进行匹配的方法。
3.1. Hausdorff相似性度量
Hausdorff距离隐含地计算了实体之间的位置和形状相似度,非常适合用于计算地理空间实体的空间相似度。
集合A和集合B之间的Hausdorff距离定义为h(A, B)和h(B, A)中较大者,如公式(1)所示。
(1)
其中h(A, B)表示从A到B的定向Hausdorff距离,h(B, A)表示从B到A的定向Hausdorff距离,它们的定义如公式(2)和(3)所示。
(2)
(3)
其中
是距离范数的一种类型。本文采用欧几里得距离。以h(A, B)为例,首先计算集合A中的每个元素ai到数据集B的最小距离,这个最小距离被定义为ai与B中的每个元素bi之间距离的最小值,然后计算这些最小值中的最大值,即为h(A, B)。h(B, A)的计算类似。
为了生成阈值从0到1的相似性度量,本文使用公式(4)将Hausdorff距离归一化。
(4)
其中H(A, B)是A和B之间的Hausdorff距离。假设RA是A的边界矩形,RB是B的边界矩形,则LD指能覆盖RA和RB的最小矩形的对角线长度。
3.2. 基于MapReduce的并行匹配框架
由于地理空间实体的几何数据具有大数据的特性,所以地理空间实体之间的Hausdorff相似性计算非常耗时。本文提出了一种基于MapReduce的并行匹配框架。
MapReduce是大型数据集并行处理的编程模型 [19] 。模型的所有输入和输出都是键/值对的形式。该模型有两个主要函数:Map和Reduce。Map接收一个输入键值对,以用户自定义的方式处理输入数据并生成中间键/值对。然后,MapReduce库将这些中间键/值对分成许多组,每组含有相同的键,并将它们传递给Reduce。每个Reduce都会接收一个键和该键的一组值,以用户自定义的方式处理它们并生成新的键/值对作为输出。
基于MapReduce的匹配方法的基本思想如下。给定两个数据集
和
,为找到A中任一实体
在数据集B中的同质实体,首先计算ai和B中的每个元素
的Hausdorff相似度,然后找到这些相似度值中的最大值,即找到br,使得Hausdorff相似度
,最后,将
与预定义的阈值进行比较,如果超过阈值,则建立ai和br之间的同质关联。
为了从数据集B中找到数据集A中任一元素的同质元素,必须计算A和B的笛卡尔乘积;即必须提取每一个可能的元素对,然后计算每一对的Hausdorff相似度。这个过程非常耗时,特别是当数据集很大时。这里提出的基于Map Reduce的并行框架可以显著地减少运行时间,提高效率。如图2所示,假设数据集A有m个元素,数据集B有n个元素,且n远大于m。数据集B使用MapReduce库分割,数据集A被加载到内存中并共享至各个节点。Map的输入是B中的一个元素bj和整个数据集A,计算bj与A中的每个实体之间的Hausdorff相似度,并输出m个键值对
,其中i的取值范围是1到m,j对于每个Map来说是一个常数。然后,Map-Reduce库将它们分成具有相同键的组,并将它们传递给Reduce。每个Reduce接收A中的一个实体a和B中的所有元素以及a与B中所有元素的Hausdorff相似度,即n个键/值对
,其中j的范围从1到n,i对于每个Reduce来说是个常数。Reduce比较接收到的所有Hausdorff相似度并找到最大值。如果最大Hausdorff相似度超过预定阈值,它将输出键/值对
。例如,假设当j等于r时,
取得最大值,输出键值对
,建立ai和br之间的同质关联。最后,RDF三元组aiowl:sameAsbr将被发布。表1指明了每个步骤中的键/值对并详细描述了该算法。

Table 1. Hausdorff similarity-matching algorithm
表1. Hausdorff相似度匹配算法

Figure 2. Map-Reduce workflow. Dataset B is split using Map-reduce, whereas dataset A is shared
图2. Map Reduce流程图。数据集B使用Map Reduce库分区,数据集A被共享
4. 实验
实验运行在八个计算节点上,每个节点有四个核、8 GB内存。每个节点上部署Hadoop,Hadoop是一个MapReduce框架的实现。
实验使用NUTS和GADM的数据来验证方法的有效性。NUTS提供欧盟经济领土的地理信息,GADM提供世界行政区域的地理信息。实验的工作流程如图3所示。
4.1. 数据预处理
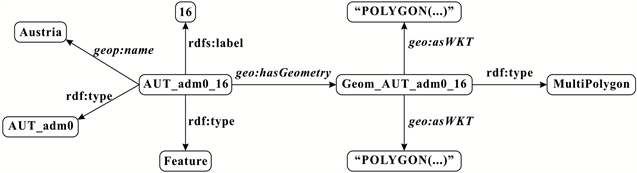
GADM发布者将其数据转换为RDF格式在GADM-RDF中发布。然而,从GADM-RDF中下载的数据仅包括属性数据,如名称,id和类型, 不包括几何数据。由于NUTS数据是欧盟经济领土数据,本文首先从GADM上下载了欧洲原始的Shapefile,然后转换为RDF。共98,493个实体。实验中的奥地利数据如图4所示。该图包含两个核心节点:AUT_adm0_16和Geom_AUT_adm0_16。AUT_adm0_16是一个名为奥地利的实体,标记为16;它是一种geo: Feature,并分类为AUT_adm0。Geom_AUT_adm0_16是表示AUT_adm0的空间范围的几何体。它是一个MultiPolygon,它的WKT (Well-known text)序列化通过谓词geo: asWKT与其本身关联。
然后,将数据上传到Hadoop分布式文件系统(HDFS),并根据谓词进行拆分。使用相同谓词的三元组被拆分成相同的文件,每个文件都以谓词命名。几何数据被分到名为geosparql#asWKT的文件,此文件将用于以后的匹配。
NUTS为欧盟提供了四个级别的粗粒度数据:NUTS0提供国家层面的数据,NUTS1提供主要社会经济区域的数据,NUTS2提供应用层面的基本区域数据,NUTS4为特定应用提供小区域数据。NUTS中奥地利的一部分数据如图5所示。由于GADM提供世界行政区域的数据,所以使用RDF查询语言(SPARQL)来提取NUTS2中的实体与之匹配。
接下来,将NUTS2中提取的数据和从GADM拆分的geosparql#asWKT文件处理成键/值对,以供Map-Reduce使用,其中键为空间实体的URI,值是其边界的坐标。
 (a)
(a) (b)
(b)
Figure 4. The data for Austria. (a) Austrian data shown in the RDF graph. (b) Austrian data shown in N-TRIPLES format
图4. 奥地利数据。(a)奥地利RDF图;(b)奥地利 N-TRIPLES格式数据
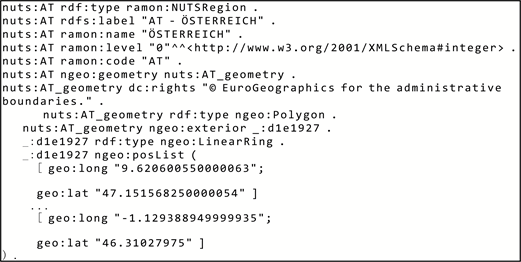
Figure 5. A portion of the Austrian data in NUTS
图5. NUTS中的奥地利部分数据
4.2. 实体匹配
将从NUTS和GADM提取的实体根据3提出的方法进行匹配。从NUTS提取的数据相对较小;因此,NUTS数据作为数据集A被加载到内存中并被共享至各个节点,而从GADM中提取的数据作为数据集B使用HDFS分割。相似性阈值设置为0.8。
4.3. 匹配结果
如表2所示,NUTS2中存在317个实体,发现了169个匹配项。其中163个是正确的。精确度定义为正确匹配数除以发现的匹配总数;召回率定义为正确匹配的数量除以NUTS2的总实体数。在表2中可以看到精确度高,召回率低,这是希望看到的现象,因为设置不正确的关联比起未找到匹配更为严重。
最后,这些匹配结果被发表为谓语为owl:same的三元组。例如,图6显示了意大利在NUTS和GADM中的数据,意大利最终发布的三元组如图7所示。

Figure 6. Illustration of the data for Italy: Data from NUTS (left) and data from GADM (right)
图6. 意大利可视化数据:左图为NUTS数据,右图为GADM数据
4.4. 运行时间和可扩展性
如表3所示,随着节点数量的增加,匹配所需的时间显著减少:当只有一个节点需要一天以上的时间进行匹配,两个节点需要11.35 h,四个节点需要5.75 h,八个节点仅需要3.17小时。图8显示了运行时间随节点数量的变化。一开始,运行时间迅速减少,随后降低速度逐渐减慢。使用八个节点可以将运行时间从多于一天减少到仅三个小时左右。

Table 3. Speedup as the number of nodes increases
表3. 随着节点增加的数据处理增速

Figure 8. Runtime as a function of the number of nodes
图8. 运行时间随节点数的变化
本实验使用了Hadoop-2.5.2。Hadoop 2.x和Hadoop 1.x之间的主要区别是引入了YARN (Yet Another Resource Negotiator)。YARN以容器为单位调度和分配集群的资源。容器是资源的封装抽象,为每个任务封装资源,如CPU,内存和磁盘。YARN为所有任务动态分配容器,每个任务占用一个容器。基于我们的Hadoop配置,一个节点可以同时存在两个容器,因此,八个节点可以同时存在十六个容器。其中一个容器被应用程序主机占用,两个节点可用容器为三个,四个节点可用容器为七个,八个节点可用容器为十五个。实验中增加节点的增速不如理论线性值(理论线性值分别为3,7和15)的主要原因是分配的任务总数为十。当使用八个节点时,十个Map任务同时运行。使用四个节点时,首先,七个Map任务同时运行,三个任务在队列中等待,有任务完成时,队列中的等待任务再启动。类似地,当使用两个节点时,同时运行三个Map任务,剩下七个任务等待,直到有其他任务完成。当所有Map任务完成后,Reduce任务就会启动。另一方面,在节点上启动任务的Hadoop开销和节点之间必要的通信也相应减少了增速值。
5. 讨论
本文提出的基于MapReduce的并行关联框架适用于一个相对较小的数据集和一个大型数据集之间的匹配,这种情况在现实世界中经常会遇到,例如,在我们的实验中使用的两个数据集NUTS和GADM,NUTS是一个欧洲小数据集,GADM是一个全球大数据集。
要执行关联任务,首先要确定某种类型的实体的标识符或描述符。显然,理想情况下,如果标识符或描述符可以唯一地标识实体,关联过程将会很简单,关联结果精度也会很高。比如,ISBN可以唯一地标识书籍,不同数据库中书籍的关联便简单准确。而对于地理空间实体,不存在与ISBN类似的可以唯一地标识实体的标识符。另外,名称重复现象在地理空间领域非常普遍,而且,一些数据集中的实体的名称属性以不同的语言呈现,例如,在NUTS中,德国的名称属性有两个,一个是德语中的德国Deutschland,一个是英语中的德国Germany。在地理空间实体的所有属性中,理论上,只有传递位置和形状信息的几何属性能唯一地识别地理空间实体。因此,本文采用Hausdorff相似性度量,它隐含地计算了两个实体之间的位置相似性和形状相似性。在未来的工作中,还可以计算名称相似度和空间相似度的加权和来建立关联,对于名称属性不局限于一种语言的,可以使用字典将所有名称翻译成对应的英文。
在匹配过程中,必须计算两个数据集中的所有可能实体对的Hausdorff距离,即两个数据集的笛卡尔乘积。因此,对于具有m个元素的数据集A和具有n个元素的数据集B,必须执行m × n个Hausdorff相似度计算。Hausdorff距离的计算是耗时的,当处理大数据集时,需要进行很多次Hausdorff相似度计算。在本文的实验数据中,如果只使用一个节点,需要一天多的时间才能完成该任务。本文提出的基于MapReduce的并行框架可以显著地减少运行时间,在八个节点上运行时,只需要大约三个小时。为了进一步提高效率,在未来的工作中,可以预定义一个距离阈值,事先筛选一遍可能的匹配,以减少需要Hausdorff相似度计算的对数,不过定义这个阈值不是一个容易的任务,不同层次的地理空间实体之间的距离是不同的,比如国家跟国家之间,城市跟城市之间,而且国内省份和省份之间的距离可能和欧洲国家与国家之间的距离大致相同。
此外,本文提出的地理空间匹配方法可以与著名的SILK框架集成,这是一个基于属性匹配的框架,基于MapReduce的并行匹配框架不仅可以用于构建同质关联,还可以用来构建其他两种类型的关联,词汇关联和关系关联,在构建另外两种关联时,Hausdorff相似度计算需要由用于其他关联任务算法代替。
6. 结论
本文提出了一种基于MapReduce的地理空间实体的并行同质关联方法。由于位置和形状信息,即地理空间实体的几何属性可以唯一地识别一个实体,本文采用Hausdorff相似性度量来计算两个实体之间的空间相似度。另外,由于地理空间数据本身很大,而且Hausdorff相似度计算十分耗时,本文提出了一个基于MapReduce的并行计算框架。实验通过匹配两个数据集NUTS和GADM检验了所提出的方法的有效性。当仅使用一个节点时,需要多于一天的时间,但是当使用八个节点并行计算时,只需要大约三个小时。此外,本文提出的基于MapReduce的并行框架除了同质关联也可以应用于其它两种类型的关联,此时,Hausdorff相似度计算需要由用于其他关联任务算法来代替。