1. 引言
随着国家对环境、占地空间和城市美观的要求越来越高,架空输电线路的数量受到了一定的限制,高压输电电缆的使用能适应国家的发展战略。高压电缆的制造工艺、敷设方式等都有可能引起绝缘掺杂、金属毛刺和裂纹气隙等缺陷 [1] ,可引起局部放电现象,使电缆温度升高,严重时还会导致绝缘损坏。
多物理场耦合仿真分析可以更真实地反映高压电缆的实际工作状态和特性规律。河北科技大学的梁永春采用实际测量和多物理场耦合数值方法对电缆温度场进行了计算,并能实时计算电缆动态载流量 [2] 。M. Rachek等人研究了磁涡流场和热场的耦合模型,运用该模型可用于分析交流电缆中的磁通密度和时空温度演变相互作用规律 [3] 。F. Yang等人针对电缆接头,研究了绝缘内部缺陷下电缆接头的电磁–热–力耦合模型,仿真分析了不同缺陷下电缆接头的热力特性,并对电缆接头不同类型的缺陷进行了表征 [4] 。华南理工大学的郝艳捧等人对海底电缆进行了电–热–流多物理场耦合仿真,分析了海水温度和不同载流量下电缆的温度分布,进而分析温度变化引起的电缆绝缘电场强度的变化 [5] 。W. Choo等人采用电声脉冲法对空间电荷进行测量,研究了不同温度下电缆的电场分布情况 [6] 。Li Zhonghua, M. R. Chen, S. Boggs等人表明,电缆绝缘的电场分布受多种因素的影响,如绝缘电导率、温度梯度、不同施压方式、湿度和绝缘内部缺陷等 [7] [8] [9] [10] [11] 。三峡大学的方春华等人对电缆接头的主绝缘划伤、连接管毛刺、半导电层剥离不齐和主绝缘杂质四种缺陷进行了有限元仿真,用于指导分析电缆接头故障缺陷类型 [12] 。多场耦合仿真、缺陷识别及表征、运行状态评估等已是高压电缆研究的重点方向,其研究成果可为电缆的设计和运行状态监测提供参考。
本文基于ANSYS仿真软件,从多物理耦合场方面研究电缆绝缘存在裂纹气隙缺陷下的电–热耦合特性。首先建立电缆的多物理场计算模型和有限元仿真模型,并进行了网格和边界条件分析;其次,仿真分析了正常运行状态下的电缆电场和温度场的分布,并对耦合仿真模型进行了验证;最后研究了不同裂纹气隙长度下电缆沿切向和径向的电场分布规律,并分析了裂纹气隙所引起的局部放电对电缆的温度分布的影响。
2. 控制方程
2.1. 电磁场控制方程
正弦电磁场基本方程组的微分形式为:
(1)
式中,
为电场强度,
为磁感应强度,
为磁场强度,
为电位移,
为电流密度,
为电荷密度。
由于工频电磁场的波长为λ = 6000 km,远大于高压电缆输电距离,因此采用准静态场分析理论对高压电缆进行计算,可忽略电磁感应项
和位移电流项
。由基本微分方程可导出其动态位的控制方程为:
(2)
式中,
为磁矢位,
为电位,求出动态位之后,可通过下式求出电场和磁场分布。
(3)
2.2. 温度场控制方程
根据傅里叶(Fourier)传热定律和能量守恒定律,可以得到二维温度场问题的控制方程,在直角坐标系中可写成:
(4)
其中,ρ为物质密度,c比热容,T为温度,l为导热系数(设各材料导热系数各向同性),Qv为内热源。稳态计算时,等式左边温度对时间的偏导数等于零,内热源Qv等于电缆导体和金属屏蔽层产生的热量,为
(5)
式中,σ为导体和金属屏蔽层的电导率,S为电流流过的等效截面积,因此需要考虑电流集肤效应,其透入深度为
(6)
式中,
为角频率,m为相对磁导率,g为电导率。
3. 10 kV三芯高压电缆有限元模型
3.1. 几何模型及材料
本文研究对象为10 kV 3 × 120的三芯高压电缆,其横截面结构如图1所示,其中1为导体,2为导体屏蔽,3为绝缘体,4为绝缘屏蔽,5为金属屏蔽,6为填充体,7为包带,8为外护套。图2为以B相的导体圆心为坐标原点建立的直角坐标系,其中R1为6.5 mm,R2为7 mm,R3为11.5 mm,R4为12 mm,R5为12.5 mm。
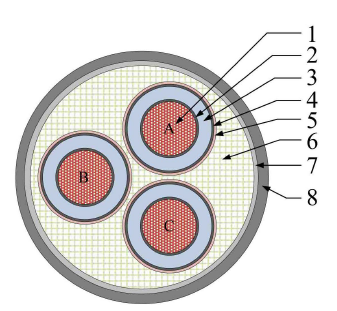
Figure 1. Structure diagram of 10 kV three-core HVAC cable
图1. 10 kV三芯高压电缆结构简图

Figure 2. Schematic diagram of Single-phase cable size
图2. 单相电缆尺寸示意图
导体和金属屏蔽层为铜,主绝缘为交联聚乙烯(XLPE),内外半导电层和包带为聚氯乙烯(PVC),填充层为聚丙烯(PP),外护套为聚氨酯(TPU),电缆使用的主要材料参数见表1。由于垂直于电缆轴向的截面都相同,本文仅对电缆截面进行二维仿真分析,可大大节约计算机资源。
3.2. 网格剖分和边界条件
1) 网格剖分
从电缆横截面看,其各屏蔽层、包带和护套均为圆环,采用扫略方式进行四边形剖分,而导体、填充体和电缆外的空气域均采用三角形剖分方式,并在流体和电缆表面的接触边界以及缺陷处加密剖分。其网格剖分如图3所示,正常情况下有160,346个节点,183,321个单元,存在裂纹缺陷时有163,125个节点,196,780个单元。

Table 1. Material parameters of Cable
表1. 电缆材料参数
2) 电场边界条件
ABC三相分别施加50 Hz的交流电压和电流激励,Ui = 10 kV,Ii = 325 A,θa = 0,θb = −2π/3,θc = 2π/3。为了防止金属屏蔽层过高的悬浮电压,每一相需要接地,外护套与大地接触,电位也为零,其余均为自然边界条件。
3) 温度边界条件
内热源Qv包括导体和金属屏蔽层产生的热量,可由(5)式求得;电缆外边界为辐射散热和对流散热,辐射系数设为0.9,换流系数设为12 W/(m2∙K),并设定其周围的环境温度为22℃。
4. 电-热耦合仿真
4.1. 电–热耦合
电缆的电–热耦合关系体现在温度的升高会降低导体的电导率,而电导率的降低会导致导体的欧姆损耗上升,又将引起温度继续升高,最终达到稳定。电导率与温度的关系如下:
(7)
其中,γ0为t0温度时的电导率,
,t为当前温度,
为1至n阶电导温度系数,忽略2阶以上的高阶项。
4.2. 模型验证
对高压电缆A、B、C三相施加有效值为8.7kV的正弦电压激励,相位相差2π/3,相序为正序,其内部各点的电场、电位和磁场都是随时间交变的。当jA = 0、jB = -2p/3、jC = 2p/3时,三相电缆电位径向分布如图4所示,图5为电场分布云图。由图4可知,A相的电位从导体到金属屏蔽层,其电位从8.7 kV线性下降为0,而BC两相导体的电位从−4.35 kV增加到0,与交流电磁理论相符合。由图5可知,电场强度都集中在绝缘层,且与半径成反比例关系,绝缘介质最大电场为20.05 kV/cm。再根据高斯定量,可导出第i层介质中的电场随半径r的计算公式
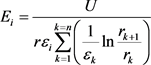 (8)
(8)
式中,n为单相绝缘介质层数,U为绝缘层的电位差。计算出绝缘介质中的最大电场为20.02 kV/cm,与仿真结果相差30 V/cm,其误差在允许的范围内。

Figure 4. Potential radial distribution of three-phase cable
图4. 三相电缆电位径向分布
由(6)式计算出集肤深度d = 9.346 mm,由于集肤深度大于半径,因此可以忽略集肤效应。把计算出的欧姆损耗作为电缆的热源,并施加温度边界条件,设置电-热耦合关系(电导温度系数为0.00392),获得电缆的温度分布如图6所示。非耦合下计算出每相电缆导体的单位长度的欧姆损耗都为13.86 W/m,每相金属屏蔽由涡流导致的欧姆损耗为0.58 W/m。由于耦合作用下温度和电导率之间的相互关系,(4)式、(5)式和(7)式会进行反复迭代计算,计算出每相电缆导体的单位长度的欧姆损耗都为16.75 W/m,而每相金属屏蔽由涡流导致的欧姆损耗为0.67 W/m。
4.3. 裂纹缺陷分析
绝缘裂纹气隙存将导致电场发生畸变,可引发局部放电现象,不同的裂纹气隙位置和长度将表现出不同的电热特性。本文对单相高压电缆绝缘开裂进行了仿真,其裂纹气隙长度d分别为1、2、3和4 mm,宽为0.5 mm。为了从切向和径向两个角度分析电场强度的变化,研究了半径为R2 + 0.25 mm的圆l1上的电场分布和直线y = 0 (R1 < x < R5)上的电场分布。
图7为圆l1上的电场分布,随着d的增加,q = p处的电场强度程指数下降趋势。图8为不同d下径向电场分布曲线,由图可知,当裂缝长度很小时,由裂纹引起的电场强度增加了,但依然低于绝缘内表面的电场强度20.05 kV/cm;随着裂纹长度的增大,由裂纹引起的电场强度继续增加,当d = 1 mm时,由裂纹引起的电场强度等于绝缘内边缘的电场强度。也就是说,当裂纹长度小于1 mm时,其增加的电场强度不易引发局部放电;当裂纹长度大于1 mm时,更易引发局部放电。图9为裂纹长度为4 mm时的局部电场分布图,裂纹气隙中的电场强度很大,在气隙尖端达到32.8 kV/cm,而裂纹与导体之间的绝缘介质中的电场强度减小。
裂纹气隙在高电场下会发生局部放电现象,持续的局部放电所引起的功率损耗有时是不容忽视的。设气隙一个周期内(0.02 s)的放电功率为196 W/m3,将该值作为气隙放电的热源,与ABC三相导体通入工频电流时所产生的热量一起仿真。图10为裂纹气隙放电时的温度分布云图,最高温度为87.8℃,比正常运行时高了21.92℃。尽管EPR的最大载流温度可达95℃,但在环境温度较高、过负荷或雷电冲击下引起局放功率变大的情况下,可能导致电缆温度超过最大载流温度,将会影响电缆的载流量。

Figure 7. Electric field distribution curve of inner surface of insulation under different crack lengths
图7. 不同裂纹长度下绝缘内表面电场分布曲线
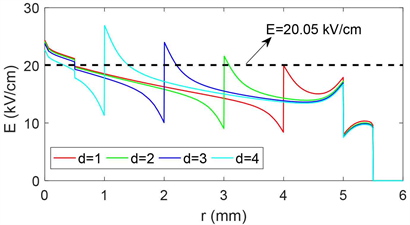
Figure 8. Radial electric field distribution curve under different crack lengths
图8. 不同裂纹长度下径向电场分布曲线

Figure 9. Electric field distribution cloud map under air gap defect
图9. 气隙缺陷下电场分布云图

Figure 10. Temperature distribution under air gap defect
图10. 气隙缺陷下的温度分布
5. 结论
本文利用有限元仿真软件对高压电缆进行了电–热仿真,分析了不同绝缘裂纹长度下的电场分布,主要研究结果如下:
1) d越长,曲线l1上2p处的电场强度减小越快,裂纹气隙中的电场强度迅速上升,d = 4 mm时,气隙电场达到32.8 kV/cm。
2) 当裂缝长度d = 1 mm时,裂纹气隙引起的最大电场等于绝缘内边缘的电场。可以这样认为,当裂纹长度小于1 mm时,电场的增大不易引起局部放电,当裂纹长度大于1 mm时,电场的增大更容易引起局部放电。因此在电缆绝缘制造的时候,考虑到操作电压和雷击过电压等,需要将绝缘内部微小气隙控制到足够小的尺寸。
3) 裂缝气隙引起的持续局部放电会导致电缆绝缘的欧姆损耗增加,导致绝缘温度比正常运行时升高了21.92℃,将会导致电缆额定载流量下降。
致谢
本论文工作得到了国家电网公司总部科技项目(内置局放传感器高压电缆系统的研究,GYW17201600045)的支持。
参考文献