1. 前言
1.1. 研究背景
当今世界,信息和网络技术的快速发展改变了人们的生活方式,根据中国互联网络信息中心(CNNIC)发布的第42次《中国互联网络发展状况统计报告》,截至2018年6月30日,我国网民规模达8.02亿,互联网普及率为57.7%。手机网民规模达7.88亿,网民通过手机接入互联网的比例高达98.3% [1] 。大量的用户聚集到移动社交网络中,人们在社交网络上表达观点、交友互动,每天都产生数亿计的信息,使其成为一个新兴的具有高度研究价值的数据源。
所以近年来人工智能、机器学习、可视化技术、统计学等各学科联立起来以期利用这个数据源,在数据挖掘与知识发现领域获得更多发展。在社交网络建模中,综合考虑用户在网站点击或搜索行为、历史记录、以及用户之间行为的相关性等多维属性信息,帮助用户在移动社交网络中排除干扰因素、实现精准推荐,并预测社交网络中用户的社交属性、准确检测出移动社交网络的社区结构,是我们希望通过研究社交网络所能实现的目标。但在实际生活中,社交网络中由于规模巨大的用户群体的存在,庞大的数据中存在大量的不确定性信息,这些也会在为用户进行定位和划分过程中产生或直接或间接的影响,因此找到一种能够较好地表达这种不确定性的模型也是目前研究迫在眉睫的任务。
基于此,本文提出利用贝叶斯网络分析和研究社交网络用户相似性。贝叶斯网络学习是贝叶斯统计的重要前沿研究方向,它是不确定性知识表达和推理的框架,可有效地描述随机变量或对象属性间的相关性和相互依赖。能够在机器学习、计算机系统等不同领域得到广泛应用,其根本原因就是贝叶斯网络是图模型与概率论相结合的产物。贝叶斯网络是用一个有向无环图来表示变量之间的依赖关系,用条件概率变量表示对其父节点的依赖关系,贝叶斯网络的每个节点都有一个对应的条件概率分布 [2] [3] 。所以它能较好地帮助反映用户行为中所蕴含的用户直接相似性及利用模型的推理能力对用户间接相似性进行计算。
1.2. 国内外研究现状
移动社交网络是一种在信息网络上由社会个体集合及个体之间的连接关系构成的社会性结构,包含关系结构、网络群体与网络信息3个要素 [4] ,因此国内外对移动社交网络的研究多集中于此三块。
而利用贝叶斯网络解决社交网络问题,目前更多的人主要集中于利用Hadoop软件中的MapReduce编程模型,因其对于大规模数据的处理更加地有效,因其软件本身即可帮助完成数据分块,对后续分布计算更加高效便捷。徐娟 [5] 等结合社交用户贝叶斯网的拓扑结构和概率推理提出了一种基于MapReduce的用户相似性度量方法。最后,利用此用户相似性度量方法发现社交网络数据中的用户相似性。李青 [6] 等利用MapReduce框架对海量广告数据进行处理,接着基于贝叶斯网构造广告关键词之间的相似模型,在接下来对存储在HBase上的大规模贝叶斯网进行概率推理,进而得到待预测广告的点击率。郭俊 [7] 等根据模块度思想,结合图论、网络性质及近似优化理论,提出了新的社区发现模型——“多社区选择模型”,并设计了新的模块度增量更新方法,算法首先计算出所有节点间的模块度增量,然后选取网络中所有具有最大模块度增量的社区进行合并,并将本文所提的模型分别在仿真复杂网络和真实复杂网络数据上,同多个算法进行了对比,验证了本文所提算法的准确性和高效性。
但目前Python编程语言的普及性及其实用性,致使本文考虑利用Python构建用户相似性贝叶斯网络。基于Python的贝叶斯网络的话,方志鹏 [8] 等提出基于贝叶斯网的新广告点击率预测方法,通过构建关键词贝叶斯网的图结构,获得与新广告关键词存在直接相似关系的关键词,根据关键词贝叶斯网近似推理算法,发现与新广告关键词存在间接相似关系的广告关键词,进而发现广告之间的相似关系,为新广告预测点击率。Yan等人 [9] 发现了点击同样广告的用户在网络上具有类似的行为,对于行为定向,使用短期用户行为来代表用户的行为会比长期用户行为来代表更有效。
2. 社交网络结构基本特征
2.1. 社交网络的理论基础
社交网络是由图表示的一种异构多关系数据集。这种图通常非常大,节点对应对象,边对应表示对象间联系或相互作用的链接,节点和链接都有属性。对象可以具有类标号,链接可以是单向的并且不必是二元的。一般认为图中的节点是社交参与者,在社交网络中任何一个社会单元或实体都可以看作节点,而边是各个参与者之间的社会关系或者交互行为,这种关系既可以是朋友关系、亲戚关系等强社会关系,也可以是因分享信息、资源等而产生的互动关系。显然,从概念可以看出,社交网络并不仅局限于像这样的在线社交网络,节点及其关系可以是传统的人与人之间面对面的交流或信件交流,也可以是现代的电话或者邮件交互,这些节点间的交互也是社会学研究的一部分。数据挖掘领域对社交网络的大多数研究在观察节点的度,即与每个节点相关联的边数,节点对之间的距离,通常是最短路径长度度量。
2.2. 社交网络的组成元素
社交网络中活动的用户是网络的基本节点,而社交网络正是由一个个用户之间相互联系而编织起来的巨型网络。网络中又可以依据兴趣爱好和关系类别的不同分为不同的组、群或圈子等社团结构。通常,把社交网络的主要组成元素归结为行动者、群体、关系和内容四类。
2.3. 复杂网络节点相关度(Node-Relevance)
在一个网络中,两个节点之间的内容相关度可以看作是其所包含内容的相似程度。如果向量i和j分别为基于词出现的页面节点i和j的内容向量,则两个节点之间的相关度可以用简单的向量之间的夹角余弦来计算 [10] :
显然,
,当两个节点的内容越相似,相关度越接近1,反之趋向于0。
2.4. 贝叶斯网络介绍
由于贝叶斯网络 [11] 只关联由某种因果依赖关系在概率上相关的节点,因此可以节省大量的计算。不需要存储所有可能的状态配置,需要存储和处理的是相关父节点集和子节点集(节点的族)之间所有可能的状态组合。这大大节省了储存空间和计算量。当然,对于今天的贝叶斯网络算法来说,有些模型还是太大了。但新的算法正在开发中,突破是有希望的。这是现代计算机科学研究的热点领域。贝叶斯网络被证明如此有用的第二个原因是它们的适应性如此强。你可以从很小的地方开始,对一个领域的知识有限,并且随着你获得新的知识而成长。此外,当我们去应用它们时,我们不需要完全了解您正在应用它的世界实例。我们可以尽可能多地利用现有的知识,而贝叶斯网络也会尽可能地利用现有的知识。
定义2.1贝叶斯网络定义
1) 存在一个变量集
,以及变量对应结点之间有向边的集合
。
2) 每一个变量都取有限个离散值。
3) 由变量对应的结点和结点之间的有向边构成一个有向无环图
。
4) 对于每个结点
和它的父结点集
,都对应一个条件概率分布表
,而且满足
其中
是
的配置。满足以上四个条件的有向无环图称作贝叶斯网络。
2.5. 贝叶斯网络推理
在给定的贝叶斯网情形下,进行贝叶斯网推理,就是对要计算的联合概率分布进行分解,通过查询贝叶斯网的条件概率表,来计算回答查询变量的概率分布。贝叶斯网推理一类典型的问题就是计算后验概率问题,即已知某些节点变量的取值,来计算其他节点变量的后验概率分布的问题。从推理的精确程度来划分,贝叶斯网的推理可以分为精确推理和近似推理两类 [12] [13] 。
理论上精确推理方法可以解决任何贝叶斯网的推理问题,由于在实际问题中,多数的贝叶斯网络结构多属于多联通图网络,运用贝叶斯网络精确推理的复杂程度随着网络节点数的增加呈指数倍增长,为提高多变量下的复杂的贝叶斯网络的推理效率,相继出现许多近似推理方法。其中包括环信念传递算法、模型简化算法、基于搜索的算法等。随机抽样算法(random sampling algorithms)便是其中最重要的一种方法之一,它的基本思想是从某个概率分布随机抽样,生成一组样本,然后从样本出发近似估计要计算的量。随机抽样算法因算法所生成的样本性质不同分为两大类,一类是产生相互独立样本的重要性抽样(importance sampling),另一类是产生相互关联样本的马尔可夫链蒙特卡洛(Markov chain Monte Carlo)算法,简称MCMC算法。本文基于构建好的贝叶斯网络的推理制,用以获取间接相似用户,故将精确推理和近似推理的一般过程说明如下。而Gibbs sampling是MCMC算法其中最基本的一种方法,所以下面就来介绍Gibbs sampling的后验概率计算。
3. 基于贝叶斯网络学习的用户相似度建模
3.1. 用户相似度贝叶斯网络模型的定义
、
和
分别为用户集合(即该社交网络中的所有作者集合)、实物集合(即该社交网络中的论文标题集合)和与实物有交互关系的用户集合,其中
,
,
表示属于用户
所著的某篇论文,用户
的所有文章以一个二元组
,
表示用户与论文之间的关系。
依据在定义2.1中我们给出一般性的贝叶斯网络的定义,此处给出用户相似度贝叶斯网络模型的定义的内容。
定义3.1 USBN用一个二元组
表示,其中:
1)
为USBN的DAG结构,每个用户对应网络结构的一个节点,用户
为
的节点集,
的取值为1或0,表示用户
是否著有文章。E为网络结构中的有向边集合,表示用户间的相似性,若用户节点之间存在相似性,则用有向边
表示,并称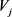 是
的一个父节点,
是
的一个子节点,
的所有父节点集合为
。
是
的一个父节点,
是
的一个子节点,
的所有父节点集合为
。
2)
为网络结构中条件概率分布的集合,由各结点相对应的CPT中的值构成,
表示结点
在其父结点发生情况下的条件概率,用来表示
的值对
的值的影响。
3.2. 用户相似性贝叶斯网络模型的构建
从给定的用户集合构建用户相似性贝叶斯网络,就是要构建用户相似性贝叶斯网络的DAG结构和计算每个节点的条件概率参数表CPT。由2.3节可知,USBN构建的关键是构建其图结构,即有向无环图的构建,这也是USBN构建的最困难的地方。一旦图结构构建成功后,便可以基于最大似然估计方法,利用USBN的有向无环图结构相对容易地计算各个关键词节点的条件概率参数表。所以我们接下来讨论图结构的构建,这包括如下两方面问题:
1) 首先需要确定判断用户是否相似,则能够明确两个用户节点间是否存在边;
2) 当明确用户节点之间存在相似关系时,接下来就需要确定用户节点之间有向边的指向。
针对问题1,判断两个用户间是否相似,对于任何两个用户,我们首先计算出与两个用户共同著作的文章数占他们各自所著全部文章数的比例,该比例越高,则表明这两个用户在社交网络中的行为相似性就越高。依据复杂网络中对于节点相似性的定义,当我们设定好阈值时,若该比值高于预先设定的阈值,则表示这两个用户是相似的,即在这两个关键词之间存在一条无向边。下面给出基于对过去所著作论文情况已知的用户相似度计算方法,用户
和
间的相似度为:
(3.1)
其中
表示用户
和
共同著作的文章,
表示共同著作的文章数,同理
表示用户
和
著作的所有文章数,
和
可基于
计算得出。假设相似性阈值为
,当
时,可认为用户节点
和
之间存在一条无向边。
针对问题2,考虑任意两个存在无向边的用户节点,比较两个用户所著文章数分别占他们各自所著全部文章数的比例,我们可以通过比较这两个比例的大小来确定指向关系。
表示用户
对用户
的影响程度,
表示用户
对用户
的影响程度,则:
,
(3.2)
其中
表示用户
所著全部文章数,
表示用户
所著全部文章数。
若
,则表示用户
对用户
的影响程度低于用户
对用户
的影响程度,则节点之间的边的指向为由
指向
。
3.3. 基于概率推理的用户相似性贝叶斯网络模型的构建
上节中,我们给出用户间相似度度量函数,可以得到相邻用户间的直接相关性,但是实际的情况是,对于网站的任一用户而言,与其相邻用户还存在一定程度的间接相似关系,所以本文中我们打算利用USBN的概率推理来获取节点间的间接相似关系,增加模型预测的准确性。由前文可知,贝叶斯网的精确推理具有指数计算时间,不能够支持高效的发现大量存在于用户之间的相似关系。目前,马尔可夫链蒙特卡罗(MCMC)算法作为一种重要的近似推理方法,已经被广泛应用于贝叶斯网推理计算,Gibbs采样是其中一种重要的马尔可夫链蒙特卡罗算法,它总是产生一条马尔科夫链,也是MCMC方法中最简单,使用最广泛的一种。基于Gibbs釆样的贝叶斯网近似推理,能够高效的计算各个关键词节点的条件概率和后验概率为高效的近似推理提供了理论基础。因此我们给出一种基于釆样的贝叶斯网近似推理的算法进行推断所有可能值的概率分布。在这里为了简化计算,对于每次的用户釆样节点,我们只考虑采样用户节点的马尔科夫覆盖中的用户节点对它的影响,即考虑采样节点的父节点,釆样节点的子节点及釆样节点子节点的其他父节点对采样节点的影响。
3.4. USBN模型构建效率测试
为了验证模型的最终效果,我们利用公式3.1和公式3.2,对于DBLP数据集 [14] 进行了试验,分别从原始数据中选择
个用户,分别测试USBN的构建执行时间。对于每一个USBN,我们记录了20次测试的平均执行时间。每次DAG构建执行时间,计算执行时间和总共执行时间都记录在图1~2中。

Figure 1. The construction efficiency diagram of USBN
图1. USBN构建效率示意图

Figure 2. The convergence effect diagram of USBN
图2. USBN收敛效果示意图
见图1,DAG构建的时间远小于CPT计算的时间,同时USBN构建的总执行时间主要取决于CPT计算执行时间。这是与实际情况一致的,节点的CPT的计算执行的时间是随着父节点的增加而呈现指数增长。从实验结果可以分析出,对于小规模数据集,在当前计算机环境条件下(类似本文实验环境),本文所提出的方法用于DAG的构建是可行的。基本上,USBN的构建执行时间随着节点数量的增加而增加。
因此,从效率的角度来看,我们可以得知通过合并数据,减少节点个数,密集型计算聚合查询处理技术在未来进一步改善构建将是可行的,这也正是我们下一步的工作。
3.5. USBN收敛性测试
为了测试算法的效率和收敛性,我们采用由部分数据集作为测试数据集生成的。随着采样次数的增多,我们记录了在不同用户个数情形下,算法每次执行时间和推理结果,并分别记录在图中。见图2,在近5000次采样以后,近似推理结果收敛于一个相对稳定的值,所以说明算法近似推理在一定程度上是有效的并且是收敛的。
在本文中,针对社交网络数据中的用户相似性发现问题,提出了一种有效的社交网络用户相似性发现方法。为了发现社交网络用户之间的直接相似性,我们通过对社交网络数据进行分析提出了一种基于贝叶斯网络的社交用户贝叶斯网构建方法。为了发现社交网络用户之间的间接相似性,我们同时考虑了USBN结构以及USBN中包含的不确定语义对社交网络用户相似性的影响,最终结合结构相似性和并行推理提出了一种基于贝叶斯网络的社交网络用户相似性度量方法。为了支持基于贝叶斯网的用户相似性度量方法的高效性和高的可扩展性,使算法更适合于海量分布式数据,我们提出利用对贝叶斯网络进行加权的方法作为改进的方向。为了测试本文所提出社交网络用户相似性发现算法的执行性能,我们利用Python执行了相关的实验,通过对实验结果分析发现本文提出的基于的社交网络用户相似性发现方法具有良好的可扩展性和较高的精确度。