1. 引言
丁家山铅锌矿是一座以铅、锌为主,伴生银、铟、镉等多种有用有色元素的有色金属矿山 [1] [2] 。随着浅表矿体开采殆尽,在矿区深边部寻找新的矿体成为制约企业发展的关键问题。为减少深部探矿的盲目性和风险性,采用合适的方法分析控矿因素、进行成矿定量预测显得尤为紧迫和重要。针对矿山深部隐伏矿体立体定位定量预测的要求,隐伏矿体三维预测成为当前矿产资源预测研究的热点领域。隐伏矿体三维预测是以大量地质、物探等资料为基础,通过地质体三维数据的获取与可视化,建立矿区数字矿产模型,开展矿体预测研究 [3] [4] [5] 。然而,面对深部找矿的实际需求,隐伏矿体三维预测一直面临着预测深度不断增大和深部有效信息相对缺乏这一对基本矛盾 [6] [7] 。因此,预测结果的可靠性随着预测深度增加而逐步降低的问题也一直存在着,这成为制约隐伏矿体三维预测持续发展与应用前景的根本问题 [8] [9] 。
重、磁、电等物探手段是获取深部地质信息的有效途径,可从不同的岩石物性角度反映地下岩矿石的赋存特征(滕吉文,2006;吕庆田,2007;董树文,2009)。本文基于丁家山铅锌矿床三维地质模型,将磁法正演技术引入隐伏矿体三维预测,通过预测模型正演磁异常与实测磁异常的差值,对隐伏矿体三维预测模型进行迭代修正,从而提高隐伏矿体三维预测模型的可靠性与准确性 [10] [11] [12] 。
2. 地质概况
丁家山铅锌矿位于梅仙矿田中南部,构成梅仙西矿田的主体。丁家山铅锌矿的矿体主要分布于龙北溪组上段绿片层地岩,矿体产状与含矿地层产状协调一致。矿床(体)产状平缓,倾向北西,倾角0˚到20˚,矿床(体)往西南方向平缓侧伏,倾角约15˚。矿体从上到下依次编号为I、II、III,其中,以位于含矿岩性段最底部的III号矿体层位规模最大,垂厚可达30 m,倾向延伸可达400 m,走向延伸达900 m,构成矿床最主要的矿体(图1)。
龙北溪上部绿片岩层中产生的矿体受不整合构造影响,当不整合面陡峭(倾斜角度为30˚)并且与下面的绿色片岩层倾斜角度过大时,在不整合面的两侧,矿体在一定范围(50 m~200 m)内变得更厚更富。在侏罗系长林组(J3c)地层中产出的铅锌矿体,主要分布于丁家山矿区第十五线西北侧,矿体位于侏罗系上统长林组(J3c)变质砾岩中的矿石矿物则以胶结物的形式分布。金属矿物主要为方铅矿和闪锌矿,含少量的磁铁矿,不含磁黄铁矿及黄铁矿。矿体倾向于不整合并且具有均匀的形状,为细长的或透镜状的。其形成和分布受不整合构造控制,可能与晚期热液构造效应有关,不整合面是控制矿体分布的主要结构。当不整合面陡倾(倾斜角度>30˚)并且与下面的绿色片岩层倾斜角度较大时,在不整合面两侧的一定范围内(50 m~200 m)有利于矿化。一方面,在不整合面结构的两侧,矿体的形成受不整合面的影响,矿体的厚度和品位趋于增加,变得更加丰富。另一方面,在不整合面结构中,还产生填充的脉状矿体。
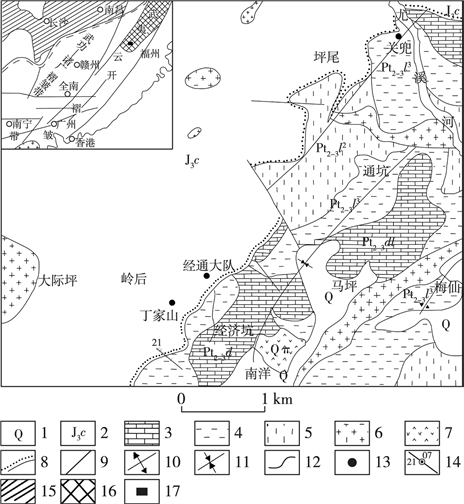 1-第四系;2-上侏罗统长林组;3、4、5-新元古界马面山岩群3-大岭组;4-龙北溪组上段;5-龙北溪组中段;6-花岗岩;7-石英斑岩;8-角度不整合界线;9-背斜;10-向斜;11-逆断层;12-压扭性断层;13-性质不明断层;14-地质界线;15-铅锌矿点;16-丁家山矿区范围
1-第四系;2-上侏罗统长林组;3、4、5-新元古界马面山岩群3-大岭组;4-龙北溪组上段;5-龙北溪组中段;6-花岗岩;7-石英斑岩;8-角度不整合界线;9-背斜;10-向斜;11-逆断层;12-压扭性断层;13-性质不明断层;14-地质界线;15-铅锌矿点;16-丁家山矿区范围
Figure 1. Simplified geological map of Dingjiashan Pb-Zn deposit
图1. 丁家山矿区及其外围地质略图
3. 矿体定位概念模型
矿体定位概念模型包括成矿环境、成矿规律到矿化分布规律(表1),指导三维矿化信息分析和矿体空间定位定量指标提取 [13] [14] 。根据丁家山铅锌矿床矿体的空间分布特征和成矿地质条件的分析与归纳,总结了丁家山铅锌矿床隐伏矿体位置预测的概念模型(该模型包括控制矿区及相关地质体中矿体分布的主要控制因素,以及地质体和矿石控制因素的建模分析方法) [15] [16] 。

Table 1. Conceptual model for ore body location
表1. 矿体定位概念模型
4. 控矿地质因素定量提取
控矿地质因素提取就是依据矿体定位概念模型,基于地质体三维模型,采用三维空间分析方法定量提取控矿因素指标,是隐伏矿体三维可视化预测方法的关键步骤 [17] [18] 。本研究采用距离场分析、趋势–起伏分析等方法,提取了不整合面距离场因素dU、不整合面趋势–起伏因素wU、不整合面坡度因素gU、不整合面夹角因素aU_S等作为丁家山矿区的控矿因素。
4.1. 不整合面距离场因素
为了定量表示不整合面距离场因素,本文基于不整合面TIN模型,利用距离场分析方法 [19] [20] ,通过分别求取块体单元到不整合面的最近距离作为距离场值(图2)。
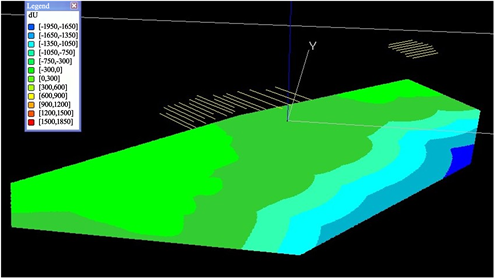
Figure 2. Unconformity surface distance field factor (dU)
图2. 不整合面距离场因素(dU)
4.2. 不整合面趋势–起伏因素
不整合面趋势–起伏分析主要揭示了不整合面起伏对不整合面周围地质空间控矿效应的影响。趋势面的提取方法包括克里金法,多项式拟合法和距离平方反比法 [21] [22] [23] 。waU和wbU分别用于表示不整合面的一次起伏(waU)和二次起伏(wbU),模型的计算结果如图3和图4所示。

Figure 3. First level undulation of unconformity surface (waU)
图3. 不整合面一级起伏(waU)
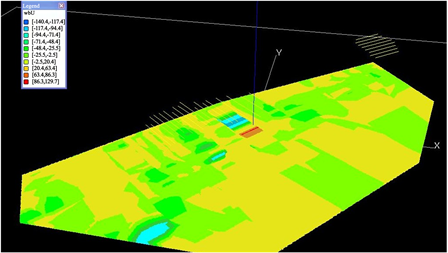
Figure 4. Second level undulation of unconformity surface (wbU)
图4. 不整合面二级起伏(wbU)
4.3. 不整合面坡度因素
不整合面坡度因素指不整合面上各点的坡度值,可以代表不整合面上各点的陡缓程度。使用TIN模型计算某点的坡度值时,该点所在的三角面片与水平面的夹角值即为该点的坡度值(图5)。
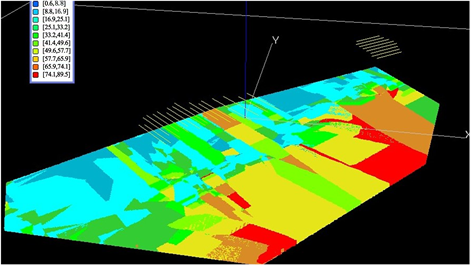
Figure 5. Slope factor of unconformity surface (gU)
图5. 不整合面坡度因素(gU)
4.4. 不整合面夹角因素
地层与不整合面之间的角度通常对成矿有影响,取立体单元与不整合面最近三角面片的夹角值,作为该单元不整合面夹角因素。计算结果如图6。
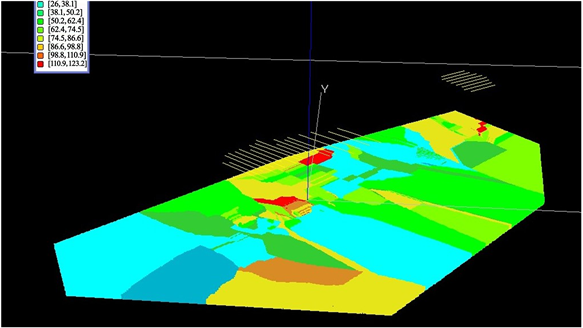
Figure 6. Angle factor of unconformity surface (aU_S)
图6. 不整合面夹角因素(aU_S)
5. 三维预测模型建立
基于丁家山铅锌矿床定位概念模型,以丁家山矿区地质体三维为基础数据,利用上述控矿地质因素定量提取方法,定量提取丁家山矿区控矿地质因素。并根据控矿地质因素与矿化指标之间的关联,建立该区域的三维预测模型。
预测模型可定量揭示矿化信息与地质空间找矿指标之间的关系,可以实现对研究区内分布的深边部矿体进行定位定量预测。矿化信息包括单元平均品位、金属量,非线性多元回归方法可以用于建立单元品位及金属量预测模型,通过建立控矿地质因素与品单元位、金属量之间的关系,表达控矿因素与矿化信息间的多元回归模型。
矿化信息与找矿信息指标的关联关系,在数学上可以表达为找矿信息指标空间到矿化变量空间的映射(毛先成等,2006),其函数化表达模型为
[24] ,MV为矿化变量空间,GV为找矿信息变量空间。由于找矿信息指标与矿化信息具有显著的线性相关性,所以该模型
可以实例化为多元线性回归模型:
(1)
式(1)中,MVk为MV中矿化变量,GVj为GV中的找矿信息指标,
为函数参数,ɛ为随机变量。参数
可以通过对GV和MV在地质空间控制区域中离散化单元的量化数据进行多元线性回归分析获得。
矿化泛函模型定量揭示了找矿信息变量与矿化变量之间的关联关系,可以用来对研究区内所有的立体单元的矿化指标Pb、Zn、PbMet、ZnMet进行估值预测。
以下为丁家山矿区各矿化指标预测结果可视化(图7~10)。
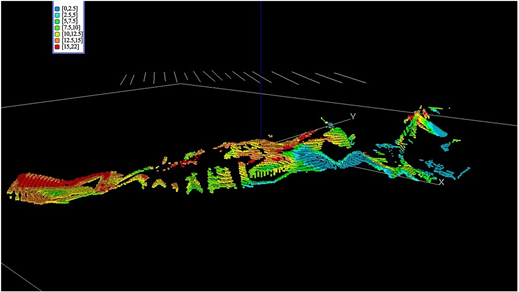
Figure 8. Prediction of Pb metal quantity
图8. Pb金属量预测图(PbMet)
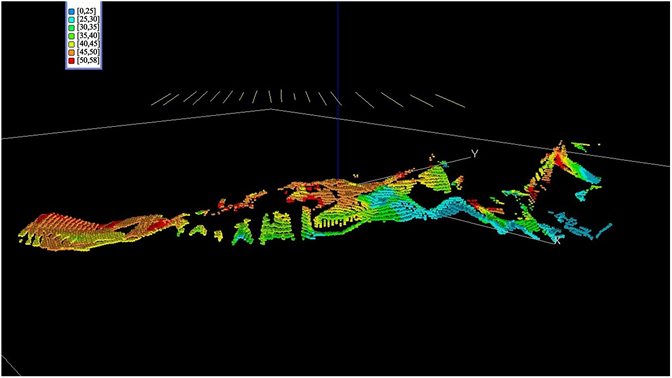
Figure 10. Prediction of Zn metal quantity
图10. Zn金属量预测图(ZnMet)
6. 磁异常驱动的预测模型修正
通过上述三维预测模型,得到丁家山矿区深部铅锌品位及金属量预测结果。然而,由于深部预测体元位于勘探工程控制范围之外,预测结果的可靠性随着深部增加而降低。针对这一问题,本文通过磁异常驱动的模型修正方法 [25] [26] ,对预测模型迭代修正,从而提高隐伏矿体三维预测模型的可靠性与准确性。
6.1. 地质模型转换为物性模型
采用三维规则网格将地质空间划分为许多小立方体,立方体划分精度取决于建模工作精度,同时考虑计算机处理的承受能力。本次研究针对研究区域模型做地球物理正演计算,考虑到计算量比较大,因此选取立体单元尺寸为10 m × 10 m × 10 m,立方体总数为274万个。
地质建模的小单元为10 m × 10 m × 10 m的规则立方体,每个立方体都有各自的空间坐标信息及岩性和物性参数(磁化率等),但是我们的正演程序的输入参数为磁化强度,因此我们需要根据建模的地质信息转化成我们所需要的参数。因此我们需要进行如下前期数据转换工作:
1) 根据磁化率求取感应磁化强度(Ji),Ji= kT0。其中T0为当地磁场,k为磁化率,参考测定统计的岩(矿)石磁性资料报告获得。据梅仙矿区勘察高精度磁测项目报告,当地磁场大小约为46368.5 nT,其中银铅锌矿的物性参数为k = 4π × 4490 × 10−6 SI,矿化绿片岩的物性参数为k = 4π × 4490 × 10−6 SI。
2) 获取剩余磁化强度(Jr),参考测定统计的岩(矿)石磁性资料报告获得。根据福建省尤溪县梅仙矿区勘察高精度磁测项目报告,项目研究中分为三种情况:
a) Pd ≥ 0.5%或Zn ≥ 1%,且(PbMet + ZnMet) > 0,则有Jr = 2.689 A/m。
b) 当条件不满足条件1时,且Pb > 0或Zn > 0,则有Jr = 0.144 A/m。
c) 当条件1和2都不满足时,则有Jr = 0 A/m。
3) 求总磁化强度(J),J = Ji + Jr。
4) 数据坐标整理,使其符合正演程序输入规则(表2)。

Table 2. Geological object physical property parameters
表2. 地质对象物性参数
6.2. 磁异常三维正演模拟
对于一般三维磁性体磁场的计算,由泊松方程可推导出如下公式 [27] [28] :
(2)
(3)
(4)
(5)
其中,
和
为磁场三分量,
为总强度磁异常。
为观测点的坐标,
为三维地
质体的坐标。M为地质体的磁化强度,I为磁化倾角,A为磁化偏角;
为地磁倾角,
为地磁偏角。一般情况下
,
。
为真空磁导率,
H/m。
对整个丁家山矿区模型进行磁法正演,得到正演结果如图11。
通过查看梅仙地区磁异常实测数据等值线图,可以看出磁异常主要分布于丁家山区域。由于丁家山矿区模型磁异常正演结果与矿区磁异常实测数据分布区域并不完全重合,只有在部分区域重合。因此我们选定部分区域作为我们的研究区域,我们将此区域的实测磁异常提取出来,如图12。
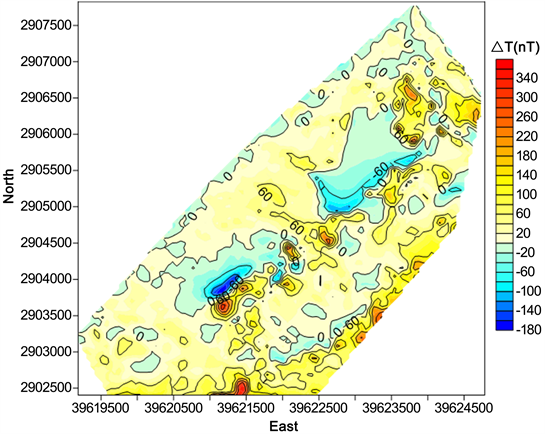
Figure 11. Magnetic anomaly forward results of Dingjiashan model
图11. 丁家山模型磁异常正演结果
6.3. 预测模型修正
利用磁异常三维正演算法 [29] [30] 对丁家山铅锌矿床进行磁法正演,获得了研究区正演磁异常,并与实测数据对比计算出两者的差异(图13)。
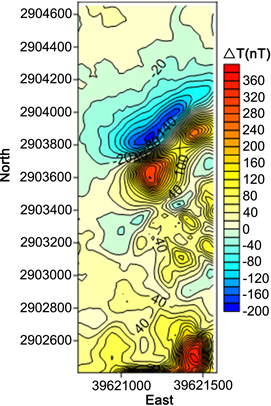 (a) 模型正演磁异常
(a) 模型正演磁异常 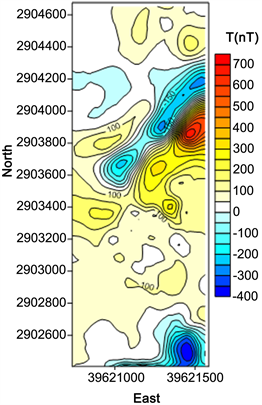 (b) 正演结果与实测数据之差
(b) 正演结果与实测数据之差
Figure 13. Magnetic anomaly of research area: (a) Model magnetic anomaly forward results; (b) Residual magnetic anomaly
图13. 研究区域磁异常:(a) 模型正演磁异常;(b) 正演结果与实测数据之差
结果显示,正演结果的异常值比实测数据小,特别是靠近研究区域边界的最大异常区域(坐标(39621500,2903900)附近区域);在等值线图的左下角,实测数据出现的是负异常,而模型正演结果是正异常,因此该位置预测结果与实际矿体相差较大,应作为我们预测模型修正的待选区域。我们将地质模型中矿体部分投影到地面,和实测数据等值线图以及化极和转化模量 [31] [32] 处理后的结果绘制在一起,通过图14就可以清晰地看到矿体分布在两个主要异常区域的正下方,坐标(39621350,2903390)处的次异常处并没有矿体分布,因此模型正演结果中此处不存在明显异常。两个重要异常中,矿体又主要集中在靠近中心区域的异常下方,而最大异常处的矿体分布明显要小,因此导致地质模型正演结果中靠近边界的异常比实际要小很多。
通过分析,模型修正应按以下规则进行:
1) 研究区域右下方应该不存在矿体,此区域实测的负异常是由研究区域右下方的矿体产生,不在建模范围内,因此不用考虑。
2) 坐标大致为(39621500,2903900)处的矿体的体积应扩大,并且其下方和右下方可能存在比已知矿体更大一些的隐伏矿体。
3) 坐标(39621350,2903390)处应该存在一个小规模矿体,其产生的正异常会保存,而负异常会被其上方的矿体产生的正异常所覆盖。
根据上述结果对三维预测模型结果进行修正,对于上述步骤选定的待选体元,修正预测体元的品位或金属量。对修正后的三维地质模型再次转为三维磁化率模型进行正演,重新计算磁异常与实测磁异常的差异 [33] [34] ,多次迭代修正,最终得到修正后的三维地质模型。实验表明,经多次迭代修正后的三维地质模型正演结果更接近实测磁异常。
7. 结论
1) 本文按照“地质信息集成–成矿信息定量提取–立体定量预测”的流程,对丁家山铅锌矿床深部体元的品位及金属量进行预测,为深部找矿提供三维可视化定位定量预测。
2) 针对隐伏矿体三维预测随着预测深度的逐渐增加,预测准确率降低的问题,本文加入了基于磁异常驱动的迭代修正步骤,对隐伏矿体三维预测模型进行修正,使预测模型更接近真实地质结构。
基金项目
国家自然科学基金项目(41472301)。