1. 引言
本文考虑了具有间接信号产生的趋化增长模型:
(1.1)
其中
是一个光滑有界区域,
。
表示飞行甲壳虫的密度,
表示做窝甲壳虫释放的化学信号浓度,
表示做窝甲壳虫的密度。山松甲壳虫的模型最早由Strohm,Tyson和Powell [1] 提出,该模型是为了研究山松甲壳虫的趋化行为。趋化行为是指由化学信号浓度梯度引起细胞的偏向运动,细胞偏向于朝化学信号浓度增加的地方移动 [2] [3] [4]。著名的趋化模型是由Keller-Segel于1970年提出 [5] ,具体表示为:
其中
是一个光滑有界区域,
表示细胞密度;
表示细胞产生的化学信号浓度。Keller-Segel模型中的化学信号是由细胞直接产出的,不同于Keller-Segel模型的是模型(1.1)飞行的甲壳虫在松树上做窝产卵变为做窝的甲壳虫产出 [6]。
当
,
时,Hu和Tao在文献 [7] 中证明了模型解的全局有界性。本文证明了
,
时,模型(1.1)解的全局有界性,其中
,
,
满足(3.7),(3.11),(3.9)。当
时,Li和Tao [8] 研究了logistic源为
时的情况,系数满足
时模型解的全局有界性,维数
时,显然
,而本文
优于其结果。在Hu和Tao研究的基础上,Qiu,Mu和Wang [9] 将飞行甲壳虫的随机扩散项
用非线性函数
来描述,考虑扩散系数
对模型的影响,当
时,假设扩散系数
得到
时模型解的全局有界性。而当
时,本文
优于其结果。当
时,Zheng在文献 [10] 中假设扩散系数
得到
时模型解的全局有界性。但是本文
时 是文献 [10] 的一个临界情况。
是文献 [10] 的一个临界情况。
本文在证明解的全局有界性时,先建立
和
一致先验估计,再建立飞行甲壳虫
的
一致估计,再由Moser迭代推得
的
一致有界性,进而根据抛物型方程Neumann边值问题的正则性理论推得
和
的一致有界性。具体地说,有以下结果。
定理1:
,假设
,
,
,
,
,
和
。存在唯一的非负函数
:
在
是模型(1.1)的经典解。特别的,存在一个常数
,使得
,
和
,
。
2. 先验估计
为了证明定理1结果,首先介绍两个基本引理用于主要结论的证明。
引理1:假设
,
,则存在正常数
使得
。
证明:在文献 [10] 中的引理2.7中有详细的证明过程。
要证明模型(1.1)的解全局有界,关键要建立
和
的一致先验估计。
引理2:假设
,对于任意
,存在正常数
,使得模型(1.1)的解
满足
,
和
。
证明:Hu和Tao在文献 [7] 中的引理2.2和引理4.4中证明了
和
的有界性。由
的有界性可以得到
,从而利用Horstmann和Winkler在文献 [11] 中的引理4.1得到
,其中
。
3. 主要结论的证明
根据引理2中的先验估计,我们下面利用引理1和Young不等式来估计
的
,
的
和
的
的有界性。
引理3:设
,若
足够大,则对于任意的
,存在正常数
使得趋化模型(1.1)的解
满足
,
和
。
证明:第一步:对于任意的
,利用
和趋化模型(1.1)的第二个方程,经过简单的直接计算可得
(3.1)
对于等式(3.1)中的I项,取
,则由
紧嵌入在
可得
, (3.2)
进一步,通过Gagliardo-Nirenberg不等式和
的有界性,则存在
使得
,
联合不等式(3.2)可得
 。 (3.3)
。 (3.3)
此外,对于等式(3.1)中的II项,利用Young不等式可知
(3.4)
另一方面,对于等式(3.1)中的III项,利用估计
和Young不等式可得
。 (3.5)
最后,利用Young不等式和引理1可得
(3.6)
联合不等式(3.1)和(3.3)~(3.6)可得
(3.7)
其中 。
。
第二步:为了处理不等式(3.7)右端的项
,对趋化模型(1.1)的第三个方程乘以
并在
上进行积分并利用Young不等式可得
, (3.8)
即
。 (3.9)
其中
。
第三步:为了处理不等式(3.9)右端的项
,对趋化模型(1.1)的第一个方程乘
并在
上进行积分可得
(3.10)
对于等式(3.10)右端的第一项,应用Young不等式和引理1可得
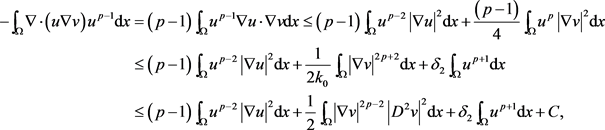
其中
。进而可得
(3.11)
现在,由(3.7) + (3.9)
+ (3.11)可得
其中
是任意给定的小常数。若
,则利用Young不等式和Gronwall不等式可得
,
和
。
事实上,若引理3中的
,则由抛物型方程Neumann边值问题的正则性理论 [12] 可得如下结论。
引理4:设
是趋化模型(1.1)的解,若
足够大,那么对于任意的
,都存在一个常数
使得
。
在引理3和引理4的基础上,我们有如下的结论。
引理5:若
,
和
是非负的,若
足够大,那么对于任意的存在
,存在常数
,使得
和
。
证明:对于任意的
,对趋化模型(1.1)的第一个方程两边同时乘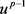 并在
进行积分,然后借助于Young不等式和引理4,容易得到
并在
进行积分,然后借助于Young不等式和引理4,容易得到
这样利用Young不等式可得
,
进一步利用Gronwall不等式可得证
。
那么在引理4和引理5的基础上,运用标准的Alikakos-Moser迭代 [13] 可得证
。
最后利用趋化模型(1.1)第三个一阶线性常微分方程的解,显然可得
。
从而定理1得证。
注1:本文在
足够大的条件下证明了方程解的全局有界性,事实上,若Logistic源项变为
,从引理3的证明可以看出,当
时,对任意
趋化模型的解全局存在,证明过程只需要简单修改即可。
基金项目
自治区青年科技创新人才培养项目“偏微分方程理论及其在图像处理中的应用”(2017Q081)。
NOTES
*通讯作者。