石英α-SiO₂晶体基本特性的原子模拟

Atomic Simulation of Basic Properties for α-SiO₂ Crystal

摘要: 采用分子动力学的方法，结合tersoff势函数，研究了石英α-SiO₂晶体融化过程以及在外载条件下完整晶体和微裂纹晶体的基本力学性能。通过体积温度曲线可以得到α-SiO₂晶体随着温度的升高体积出现了前期的急剧膨胀和后期的缓慢增加，直到趋于稳定的变化，说明在升温过程中α-SiO₂晶体出现了结构的变化。同时研究了α-SiO₂在常温单轴加载下的力学性能，研究结果表明α-SiO₂晶体在加载过程中经历弹性变形、塑性变形以及断裂变形三个阶段，其中获得的完整晶体的屈服强度为22.6 GPa，断裂强度为36 GPa，说明α-SiO₂晶体具有很好的强度。而微裂纹晶体的屈服强度为20.7 GPa，断裂强度为20 GPa，表明α-SiO₂晶体断裂方式为脆性断裂。

Abstract: The melting process and the basic mechanical properties of perfect crystal and microcrack models for α-SiO₂ crystal are studied with tersoff potential function under external loading by molecular dynamics simulation. The volume-temperature curve shows that the volume of the α-SiO₂ crystal shows a sharp expansion in the early stage and a slow increase in the later stage with the increasing of temperature, until it reaches a stable change, which indicates that the structure of the α-SiO₂ crystal changes during the heating process. At the same time, the mechanical properties of α-SiO₂ under uniaxial loading at room temperature are studied. The results show that the α-SiO₂ crystal experiences three stages of elastic deformation, plastic deformation and fracture deformation during the loading process. The yield strength of the perfect crystal is 22.6 GPa, and the fracture strength is 36 GPa, indicating that the α-SiO₂ has good strength. But the yield strength and fracture strength of the microcrack model of α-SiO₂ are 20.7 GPa and 20 GPa, respectively, which show that the fracture mode of the α-SiO₂ crystal presents brittle fracture.

1. 引言

α-SiO₂是石英物质和硅酸盐的重要组成部分，而且是地球上储量最丰富的物质。石英晶体在常压下有多种晶体结构：如α-SiO₂，β-SiO₂，α-磷SiO₂，β-磷SiO₂以及α-方SiO₂，β-方SiO₂等等。其中石英α-SiO₂是常温常压下最稳定的晶体。对于α-SiO₂的研究通常是采用实验的方法观测其在高压下非晶化的相变。如王德军 [1] 研究了α-石英在高温高压下的结构转变，指出α-石英在高温高压下合成小尺度的柯石英；Palmer等 [2] 通过研究α-SiO₂在常温下的加压相变过程，发现了石英相变的规律；张广强等 [3] 通过机械球磨研究了α-SiO₂在高温高压下的结构转变以及形成柯石英的实验条件；Dubrovinsky等 [4] 研究了α-SiO₂的高压相变，得到了类似α-PbO₂结构的石英相，而且还发现应力在25 GPa到35 GPa之间时会出现非晶化转化，卸载压力后完全非晶化。但是，近年来随着计算机技术的飞速发展，应用分子动力学的方法，通过大规模并行计算研究晶体材料的力学性能、结构转变以及物理特性等方面成为可能 [5] [6] [7] [8] [9] 。如潘海波等 [10] 通过分子动力学的方法利用Morse势模拟了α-SiO₂的高压相变，指出晶体在高于24.6 GPa时出现非晶相变，其计算结果与实验结果较一致。因此，计算机模拟实验为研究晶体的力学性能开辟了另一条有效的途径，可以为实验研究提供理论支撑。

本文应用分子动力学的方法研究了石英α-SiO₂晶体的融化过程和单轴拉伸的力学性能，通过分析随着温度的升高体积变化曲线以及应力应变曲线的变化，探讨石英α-SiO₂随着温度的升高结构的变化过程，同时通过讨论加外载时应力应变曲线的变化规律，分析了其基本力学性能，而且还探讨了裂纹对拉伸力学性能的影响，综合评价石英α-SiO₂的基本的物理特性。

2. 模型和方法

2.1. 模型

图1为石英α-SiO₂的晶体结构。在二氧化硅中，硅位于正四面体的中心，4个氧原子位于正四面体的4个顶角上，图1(a)表示二氧化硅在体心立方结构中的晶胞。然后根据笛卡尔坐标构建立了α-SiO₂的晶体结构(如图1(b)所示)。其中，晶格常数a = 4.978埃，b = 4.978埃，c = 6.948埃，盒子的长度为30a × 30b × 30c，总的原子数为324,000个，在xyz三个方向上采用周期性边界条件。

Figure 1. α-SiO₂ crystal model

图1. α-SiO₂晶体模型

2.2. 模拟方法

在分子动力学的模拟过程中，我们采用的tersoff势函数 [11] 描述Si-O之间的相互作用。然后在NPT系综下，时间步长1 fs，应用Nose-Hoover热浴的方法 [12] [13] 在常温下进行弛豫，弛豫步数20,000步。图2为模型弛豫过程中能量变化图，从图中可以得到晶体模型在10 ps后达到平衡。然后在NVT系综下进行单轴加载，应变率为1 ´ 10⁹ s⁻¹，这时仍用Nose-Hoover热浴的方法控制系统的温度使其保持在相应的温度条件下。然后在常温300 K下模拟石英α-SiO₂晶体的拉伸力学性能。模拟结果讨论分析中我们应用CNA结构分析方法 [14] 来分析体系中微观结构的演变，利用Ovito软件观察原子结构，应用LAMMPS代码 [15] 来模拟拉伸力学性能。

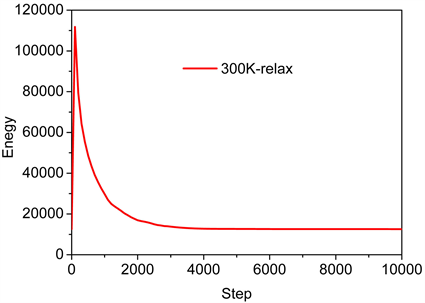
Figure 2. Diagram of energy change during model relaxation

图2. 模型弛豫过程中能量变化图

3. 结果与讨论

3.1. α-SiO₂体积随着温度升高的变化曲线

图3为α-SiO₂的体积温度曲线。从图中可以得到随着温度的升高晶体的体积出现了A和B两个变化拐点。在A点时，晶体从四面体结构中逐渐的析出非晶结构。随着温度的升高，体积以非线性的形式快速的膨胀，晶体的非晶化程度比重也迅速的增加。到了B点时，整个晶体结构完全非晶化，晶体结构趋于稳定，然后随着温度的升高晶体的体积缓慢稳定的增加，结构逐渐进入融化阶段。

Figure 3. Volume temperature curve

图3. 体积温度曲线

3.2. α-SiO₂晶体在外载下的力学性能

图4为石英α-SiO₂的完整晶体在常温下单轴拉伸的应力–应变曲线。应力–应变关系反映了材料的基本力学性能，从图中可以得到随着应变的增加石英α-SiO₂晶体在应变为4.7%时出现了弹性极限(如图4中A点)，应力与应变表现出非线性关系。A点后晶体进入弹性变形阶段，应力与应变呈线性关系，此时材料结构没有发生形变。当加载的应变到达32.6%时，晶体的内部应力达到第一个屈服点，屈服应力22.6 GPa。随后晶体进入塑性变形阶段，然后随着外载的逐渐增加，从图中可以得到应力在B点和C点之间出现了上下震荡，纳米晶体进入塑性变形阶段，而且开始发生非晶化相变。应力过了C点之后，由于晶体结构完全非晶化，随着加载的进行，应力逐渐增加，一直达到曲线的锋值——断裂强度(36 GPa)，晶体开始进入断裂阶段。接着随着应变的增加应力急速下降到零，此时晶体完全断裂。因此，从图中可以看出，石英α-SiO₂晶体在常温单轴拉伸过程中经历了弹性阶段，塑性阶段(非晶化相变)以及断裂阶段，弹性模量达到了69 GPa，具有很高强度。

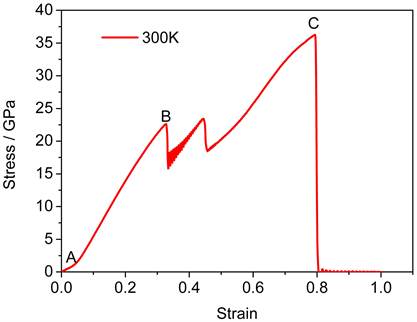
Figure 4. Stress-strain curves of α-SiO₂ crystal under uniaxial tension

图4. α-SiO₂完整晶体在单轴拉伸下的应力–应变曲线

3.3. α-SiO₂晶体中裂纹扩展的力学性能

图5为石英α-SiO₂在常温下裂纹模型单轴拉伸时的应力–应变曲线。从图中可以得到随着应变的增加石英α-SiO₂裂纹晶体在应变为31.8%时，应力达到最大的屈服点，屈服应力20.7 GPa (如图中A点所示)。相对于完整晶体的屈服应力和屈服应变出现了下降(如表1所示)。由此可以得到微裂纹可以降低石英晶体的力学性能。然后晶体由弹性变形阶段进入塑性变形阶段，随着外载的逐渐增加应力在A点和C点之间进行上下的震荡，石英晶体结构展现出很好的塑性，能延缓微裂纹的快速扩展，同时纳米晶体结构也开始发生非晶化相变。当加载应变过了C点之后，由于晶体结构完全非晶化，随着加载的进行，应力逐渐增加，一直达到曲线的锋值——断裂强度(20 GPa)，晶体开始进入断裂阶段。这个数值远远低于完整晶体结构。因此，微裂纹使晶体的断裂强度出现大幅度的下降，这主要是由于结构的非晶化降低了结构的塑性，使得裂纹尖端的应力集中现象得不到有效的缓解，裂纹进入快速扩展阶段，接着随着应变的增加应力急速下降到零，直到晶体完全断裂。

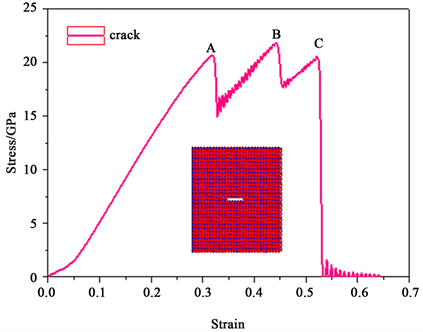
Figure 5. Stress-strain curves of α-SiO₂ central crack model under uniaxial tension

图5. α-SiO₂中心裂纹模型单轴拉伸下的应力–应变曲线

Table 1. Comparison of basic mechanical properties between complete crystal and crack model

表1. 完整晶体和裂纹模型基本力学性能的对比

4. 结论

本文应用分子动力学的方法，结合teroff势函数，模拟了石英α-SiO₂晶体基本的物理特性。首先通过升温，得到了温度体积变化曲线。然后研究了α-SiO₂在常温单轴加载下的力学性能，从应力应变曲线得出晶体在加载过程中经历弹性变形、塑性变形以及断裂变形三个阶段，屈服强度为22.6 GPa，断裂强度为36 GPa，在塑性变形阶段观察到了α-SiO₂从晶相向非晶转化的相变过程。然后构建了α-SiO₂中心裂纹模型，对比分析了其裂纹模型和完整晶体模型基本力学性，研究结果表明微裂纹导致α-SiO₂晶体的屈服应力和屈服应变下降，并引起断裂强度的极具下降，说明裂纹在扩展过程中加剧材料内部的破坏。

基金项目

湖南省自然科学基金省市联合基金项目(批准号：2016JJ5002)，湖南文理学院博士启动项目(批准号：16BSQD05)。