1. 引言
涡环作为由涡管封闭而形成的自由涡量分布组成的最基本涡结构,自19世纪50年代被Helmholtz发现,就成为了流体力学研究的热点 [1] 。对涡环相关特性的研究是人们研究涡动力学基本原理的主要手段。
Maxworth [2] [3] 通过活塞装置产生涡环并研究了其生成与演化的过程。Didden [4] 建立了Slug模型描述了射流产生的涡环的物理特征。Shariff等 [5] 和Lim等 [6] 对之前的在静止、非分层环境中涡环的动力学特征进行了总结。Gharib等 [7] 通过对活塞–圆管装置产生的轴对称涡环的形成过程进行研究,发现了涡环
生成过程中的夹止现象,即当冲程比L/D (L为活塞运动距离,D为管口直径,也就是形成时间(
)
达到一个临界值
时,涡环开始逐渐与后续射流主干分离,即发生夹止(Pinch-off),之后从出口分离的剪切层涡量不再会被涡环吸收,涡环的生长达到最大状态。Gharib等人 [7] 认为起动射流中涡环生长的最大状态对应着某种流动属性的最优化。之后,Krueger和Gharib [8] 证实了在其对应的时刻,射流的时均推力达到最大值。
随着光学测速技术的发展,对涡环结构,特别是涡核的研究更加细致与准确。Weigand等 [9] 发现层流涡环内涡核的涡量符合高斯分布。Norbury [10] 根据无量纲的涡核半径对涡环进行了分类。Fraenkel [11] 在1970年对细核涡环建立了运动力学模型。Saffman [12] 、Sullivan [13] 等对细核涡环的模型进行了修正与完善。
浮力涡环作为一种环内流体与环境流体密度不同的涡环,其生成与演化过程受到浮力影响的研究结果还存在争议。早前对浮力涡环的研究主要集中在其远流场的流动特征。Turner [14] 在1957年研究了正浮力涡环在其形成后期的动力学特性,并建立了湍流浮力涡环的理论模型。提出浮力在涡环向上运动的过程中起到的主要作用是保持涡环结构稳定、增加涡环半径的增长率和减少涡环的行进速度。之后,Turner [15] 建立了起动羽流的理论模型。
近年来,受到Gharib等人 [7] 在起动射流中发现涡环夹止现象的启发,人们对起动浮力射流在初始阶段以涡环为主要流动结构的近流场动力学特性进行了一些较为系统的研究 [16] 。Pottebaum和Gharib [17] 首次在有加热底部圆盘产生的起动羽流中观察到了浮力涡环的夹止现象。该流动可以看作是起动浮力射流在出口处动量通量 减少为零的极限情况,其所有动力学变量(环量、动量和动能)都由浮力产生。该研究表明了起动浮力射流中涡环夹止现象的存在。Bond和Johari [18] 通过在环境流场中向下释放有限体积的重流体,研究了起动浮力射流在近流场的动力学特性,发现浮力产生的斜压性改变了涡环的结构和发展。Marugán-Cruz [19] 等通过实验研究了负浮力对射流的影响,发现当雷诺数足够大,而且密度与粘性的比接近一样,流体的特征就只与密度傅汝德数相关,其中Ri代表理查德森数,是浮力射流中浮力与初始动量相关的参数。其表达式为:
(1)
公式中D为圆管直径,Up为活塞速度,
,
为外部流场密度,
为管内流体密度,g为重力加速度。
当
时,随着Fr的增加,形成数也随着增加,最后达到均质射流的值3~4左右。也就是说相对于均质射流,负浮力射流的形成数减少了。与之相对应的Wang [20] 等通过对正浮力射流的数值模拟研究,发现正的浮力增加了其形成数。Gao [21] 等通过数值模拟,研究了
的浮力射流,并确定了形成数F与分离数S随Ri变化的规律。其中,分离数S是当尾流与前导涡环完全分离时的无量纲时间。在理论研究上,Shusser与Gharib [22] 对起动浮力羽流中涡环演化建立了积分模型,对其浮力涡环的形成数进行了预测。
本实验目的为研究小冲程比(L/D = 2、3)条件下,负浮力射流产生的涡环在近流场的演化与发展规律,并揭示负浮力涡环生成与演化受起动射流理查德森数影响的物理机理。
2. 实验部分
该实验装置由水箱,铝合金架,活塞–圆管装置,撞针,伺服电机,相机,激光发生器组成,如图1所示。其中水箱由有机玻璃制成,其尺寸为0.8 m × 0.8 m × 1.2 m,下方开口方便排水,并被置于铝合金架上固定,水箱中盛放环境流体,用于浮力涡环的生长与演化。
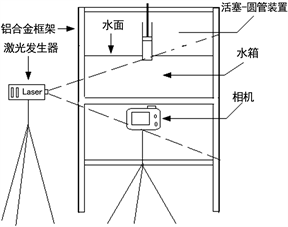
Figure 1. Starting buoyancy jet device
图1. 起动浮力射流装置
整个涡环的发生装置由活塞–圆管装置,撞针,两个伺服电机,倍福PLC控制器,丝杆以及钢板框架组成。其中,圆管直径D0 = 200 mm,活塞最大运动长度Lmax = 220 mm,两个伺服电机位于整套装置的上方与两根丝杆连接,两根丝杆分别套有活塞与撞针。PLC控制器与电机、计算机相连,负责控制器将控制电机的运动,从而实现对活塞与撞针的控制。实验开始后,撞针向下快速运动刺破薄膜,然后迅速向上运动到离活塞面2 mm处,然后同活塞一起向下运动。
相机与激光发生器作为PIV技术中的主要设备,发生器用于照亮流场,相机用于拍摄流场照片。在该实验中使用的相机型号为IMPERX-B1620M,图像记录最大为47帧/s,每次记录图像500帧,图像分辨率为1600 × 1200像素。在PIV数据处理中,选取的最小处理窗口为32 × 32像素,步长为16像素。管内流体为酒精溶液,实验开始前管内外都要布上适量示踪粒子。通过输入控制程序的函数控制伺服电机,从而驱使活塞运动。该控制装置精度高,瞬时达到设定速度并一直以匀速运动,最后也在极短时间内停止,故活塞的运动可以看做匀速运动。
表1列出了射流的不同条件,其中H1、H2是内外密度相同的均质射流,N1-N8是负浮力射流。该实验中,所有实验情况下
。
3. 结果与分析
在第一部分对两组均质射流,八组浮力射流通过实验测得的数据得到的涡量场,速度场选取了一定的时刻(
)展示。并对
四个时刻,在涡核所处 位置的涡量分布进行了对比。在第二部分,展示了涡环半径以及涡核位置的变化情况。第三部分则对涡环的动力学物理量(环量、冲量、速度),进行了对比与分析。
3.1. 涡量场与速度场
在下列图2中图2(a)~(c)、图2(d)~(f)分别代表L/D为2和3的均质射流在不同时刻的涡量等值线与速度矢量图。对比以后,可以发现其生长机制几乎相同,都是在活塞开始运动后,流体被推出圆管,在管口处形成分离剪切层进而卷起形成涡环,在一定时间涡环离开管口,开始向后运动如图2(a)、图2(d)所示。活塞继续推动管内流体进入涡环中,活塞停止推动后,涡环继续向前运动,如图2(b)~(f)所示。此时,我们还可以观察到管口处出现了与涡环相反的涡量,这就是制止涡环,是由于活塞的突然停止产生的。由于活塞多推动了20 mm,在冲程比为3的均质射流,
时刻,仍有尾流,可以通过该时刻的速度矢量图观察到,说明涡环在继续增长,且通过涡量等值线的位置直观对比可以看到涡环在
达到4.05后,其运动速度发生了变化。最后两个时刻的涡量等值线的对比可以发现L/D = 3的涡环半径,涡环大小都是大于L/D = 2时的涡环,说明在达到形成数之前涡环都是在增长的。
图3、图4分别是
,L/D = 3条件下,在不同时刻的涡量等值线与速度矢量图。选取L/D = 3的情况做分析,是由于在该冲程比下活塞运动的距离更长,可以观察到涡环变化的时间更长。
对比图2(d)~(f)与图3(a)~(c)的涡量等值线,可以发现浮力涡环在活塞推动的过程中其生长机制与均质射流产生的涡环相同,都是先在管口卷起并形成涡环,然后涡环离开管口向后运动。只是与均质射流产生的涡环不同之处在于,浮力涡环在活塞推动过程中半径显然相对的要大一些。但在活塞停止运动以后,有负浮力的射流产生的涡环的半径小于均质射流产生的涡环,且涡环的移动速度也减小。这些结论也可以对比不同理查德森数条件下的浮力射流得到。还发现均质射流产生的涡环在形成时间较长的情况下与其停止推动活塞的时刻几乎保持不变,但浮力涡环却在不断发生变化。且理查德森数越小,涡环半径越小,移动速度越慢,说明浮力对涡环的成长演化过程起到了重要的作用。
在Ri = 0的情况下,由于没有浮力,故涡环周围不会观察到与涡环内相反符号的涡量。当Ri = −0.05,时,可以在t* = 4.05时刻(如图3(c)所示)看到涡环前段有很小的负涡量区域,说明在该情况下负浮力开始通过斜压效应产生负的涡量,对涡环的演化产生影响。随着Ri的减小,在Ri = −0.1的条件下,在涡环生成的过程中,涡环的周边就出现了相反的涡量,在活塞停止推动后,尾部开始出现浮力产生的相反的涡量,如图3(f)所示。对比观察速度矢量图,我们可以看到有向上的速度矢量,说明有轻质流体向上运动,这就是等值线中尾部出现与涡环相反涡量的一个重要原因,这些与相反的涡量这会使整体的环量下降。这一情况在Ri = −0.2与Ri = −0.3的条件下更为明显,如图4所示,甚至到t* = 4.05后浮力涡环逐渐消散,流体向上运动。在t* = 7.8时刻甚至产生了与射流方向相反的涡,这可能是由于轻质流体撞击管口有机玻璃产生的。如图4(c)、图4(f)所示。
通过对涡量等值线和速度矢量图的简单分析,能分析得出理查德森数的主要影响是通过负浮力作用使涡环整体运动速度减小。另外,在涡量等值线中,可以看到涡环的涡量在发展的过程中基本集中在涡核的位置,故而在后续对其各动力学物理量进行计算和对比时,可以参照细核涡环物理量的积分公式进行分析。通过涡量等值线与速度矢量图,对涡环的演化过程进行定性地分析,即能观察到其位置,是否有相反涡量以及轻质流体向上运动的情况。在定量的分析上,能发现在没有浮力的情况下,涡环在
时的无量纲半径约为0.55,而有浮力的所有情况其半径都约为0.65,差别不大。说明浮力对浮力涡环的影响之一是增加涡环生长过程中的半径。还可以说明浮力在涡环早期生成中影响没有后面时刻影响明显,分析后发现是轻质流体的体积过少,流体受到的斜压效应并不明显。
从涡量场的数据中,可以得到其涡核处的涡量分布,有助于我们更直观的对涡环的特性以及浮力对涡环影响进行分析与讨论。
将涡核所处位置在r/D方向,
时刻的涡量分布进行对比,发现在L/D = 2的条件下,随着理查德数减小,最大涡量逐渐减小。且随着形成时间t*增加,理查德数越小,最大涡量的值减小得越快,如图5(c)、图5(d)所示。在L/D = 3的情况下的涡量分布如图6所示,其最大涡量值在r/D方向的位置的变化没有L/D = 2条件下的涡量分布变化明显,说明稍大冲程比的情况下,浮力对涡环内部涡量分布的影响小一些。
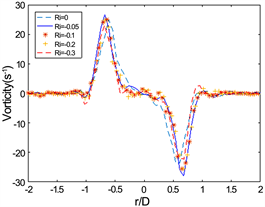 (a) t* = 3.3
(a) t* = 3.3  (b) t* = 4.05
(b) t* = 4.05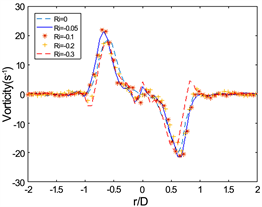 (c) t* = 4.3
(c) t* = 4.3  (d) t* = 5.55
(d) t* = 5.55
Figure 5. The vorticity distribution at different moments through the X/R position of the vortex core, while L/D = 2
图5. L/D = 2,通过涡核的X/R位置在不同时刻的涡量分布
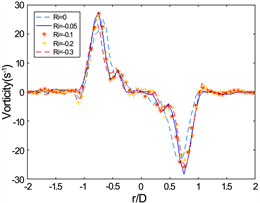 (a) t* = 3.3
(a) t* = 3.3 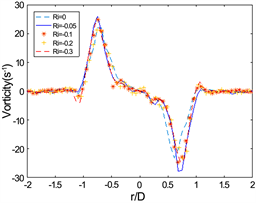 (b) t* = 4.05
(b) t* = 4.05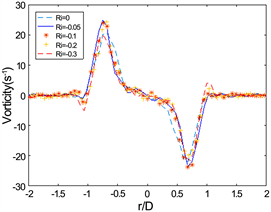 (c) t* = 4.3
(c) t* = 4.3  (d) t* = 5.55
(d) t* = 5.55
Figure 6. The vorticity distribution at different moments through the X/R position of the vortex core, while L/D = 3
图6. L/D = 3,通过涡核的X/R位置在不同时刻的涡量分布
在存在浮力的情况下,前两个时刻,两个冲程比的涡量分布相似,在涡核周围的涡量大小以及分布情况在所有条件下都几乎是相同的,但在后两个时刻明显的发生了变化,其最大涡量下降,最大涡量在r/D方向向0移动,说明了浮力对涡环的涡量影响不是瞬时产生的。同时也能清晰的看到涡环外部与涡环中符号相反的涡量也随着时间在增加,这说明斜压效应的影响是随着涡环运动增大的。
通过对比图5(c)、图6(c)和图5(d)、图6(d),可以发现,在涡环外部产生的与涡环内部相反的涡量,在分布上是相同的,即宽度相同,最大(最小值)也一样。通过这一现象我们可以推断出一个结论:涡环周边由斜压效应产生的与涡环内部涡量符号相反的涡量,其分布与冲程比无关,只与Ri相关,在Ri相同的情况下,其最大(最小)值随时间增大(变小),其宽度随时间增大。
3.2. 涡核位置与涡环半径
图7(a)~(e)分别是
的涡核位置分布图,蓝色圆圈代表是L/D = 2的涡核位置,红色菱形代表的是L/D = 3的涡核位置。可以发现,随着活塞推动,涡核位置在X、Y方向不断增大,在活塞停止推动后,均质射流的涡核位置在r/D方向上基本不变的,而对浮力射流而言,随着浮力增加,涡核在r/D方向的位置逐渐减小,在X/D方向还是在增加。但在浮力比较大的情况下(即
),涡核位置在X/D = 1.2左右处就不再增加,说明涡环不继续在X/D方向运动。而且涡核在该处产生往复,这里通过与涡量等值线对比发现是涡环在浮力作用下消散的过程。由于选取的是相同时间内涡核的位置变化,故而可以发现冲程比为3相较于等于2的实验下,涡核位置在 方向运动得更远,这也是符合实际情况的。通过图7,还可以发现,两个不同冲程比下的涡核位置在最初几乎是重合的,这说明在冲程比为3时,涡核的位置变化在形成时间为2之前与冲程比为2的变化情况相同。
 (a) Ri = 0
(a) Ri = 0 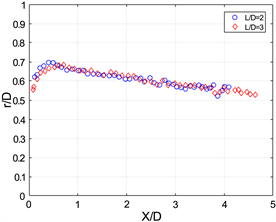 (b) Ri = −0.05
(b) Ri = −0.05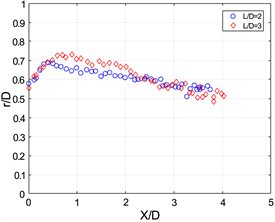 (c) Ri = −0.1
(c) Ri = −0.1 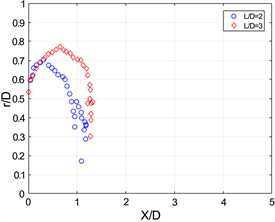 (d) Ri = −0.3
(d) Ri = −0.3
Figure 7. Vortex core position at different Ri
图7. 不同Ri涡核位置的分布情况
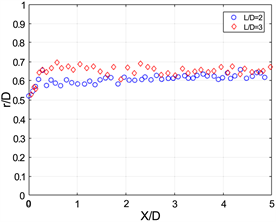
图8是无量纲涡环半径随形成时间t*的变化情况,在这里我们以涡核的位置到管轴线位置的距离为涡环的半径。再将涡环的半径以管的直径对其无量纲化,得到无量纲涡环半径。可以发现涡环出现的位置都是在离管口(r/D = ±0.5)一定的距离处,所以涡核位置开始并不是在管口的。从图中我们还可以得到均质射流在L/D = 2、L/D = 3的无量纲涡环半径R*分别为0.6,和0.65,并且在活塞停止推动后其半径随时间变化不大。对于浮力涡环半径,可以发现在活塞停止后,其半径是大于均质射流产生的涡环的,大约是在0.7~0.8,所以可以说明浮力的一个作用,即在生成涡环过程中增加涡环半径。从图8中还可以发现,在冲程比为2时,浮力涡环半径在活塞停止的时刻(t* = 2)半径都是在0.7,而在冲程比为3时,活塞半径在活塞停止时刻(t* = 3)随着理查德森数减小而增大。
 (a) Ri = 0
(a) Ri = 0  (b) Ri = −0.05
(b) Ri = −0.05 (c) Ri = −0.1
(c) Ri = −0.1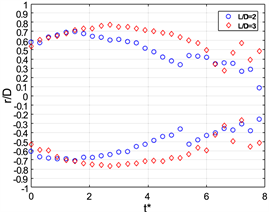 (d) Ri = −0.3
(d) Ri = −0.3
Figure 8. Dimensional vortex ring radius versus formation time t*
图8. 无量纲涡环半径随形成时间t*的变化情况
而在活塞停止运动以后,涡环的半径开始明显下降,对图8(d),可以发现L/D = 2情况下,涡环的半径随形成时间先减小,到了t* = 5.6左右,其半径又变大,这是由于涡环在浮力作用下变形消散引起的半径变化。
在该部分分析了涡环的半径随形成时间变化以及涡核位置变化的情况。发现在活塞推动过程中,即涡环生成的过程,负浮力增大了涡环半径。这一结果与活塞停止推动后的相反,浮力在活塞停止推动后减小了涡环的半径。也从涡环半径和涡核位置的图中能分析到涡环在小的理查德森数条件下消散的情况。
3.3. 涡环的环量、冲量与速度
首先定义特征长度为管口直径D,特征时间
。参考Ghrib [6] 对水力冲量和环量的计算公式:
(2)
(3)
我们可以利用实验数据求得涡环的环量值。再利用Slug模型中环量的计算公式:
(4)
得到特征环量
,从而得到无量纲的环量
,如图9所示。
 (a) L/D = 2
(a) L/D = 2  (b) L/D = 3
(b) L/D = 3
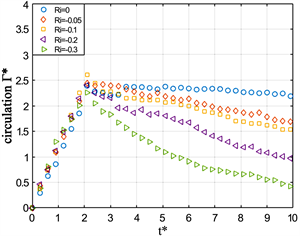
Figure 9. Dimensional circulation Г* versus formation time t* at different stroke ratio
图9. 不同冲程比下Г*随t*变化的情况
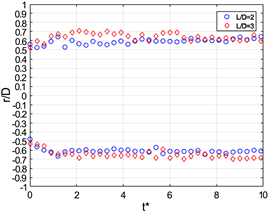
可以发现在冲程比为2时,环量在活塞停止以前增加的速率相同,且都在活塞停止的时刻达到最大值2.5。而在冲程比为3时也是在活塞停止时的环量达到最大,但其环量最大值随着理查德森数的减小(浮力增大)而减小。所以,可以推断在冲程比为2的情况下浮力在涡环生长过程中对涡环环量的影响很小。同时发现,随着理查德森数减小,在活塞停止后,涡环环量减小的速率与之成正相关。
对比图9(a)、图9(b)还可以发现以下规律:第一,在L/D = 3,不同理查德森数情况下环量的变化在形成时间2.3之前都是相同的。第二,对比L/D = 2与L/D = 3条件下环量随时间的变化,发现在所有有浮力的情况下,环量的减小速率都是L/D = 3的更大,主要原因是推出的轻质流体更多,受到的浮力更大。所以环量的变化也更大。
在Fraenkel [10] 的细核涡环建立的运动力学模型中,其中的冲量与速度公式如下:
(5)
(6)
对冲量的分析中,首先确定特征质量
,特征冲量为
。
选取L/D = 2在不同Ri下的条件分析,使用公式(2)中的冲量公式利用实验数据求得冲量Iw,再将求得的环量与半径带入公式(5)中,可以得到冲量Ic,将两个值无量纲化后(
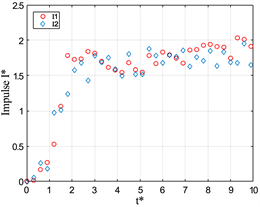
)对比,如图10,发现其变化是符合细核涡环的动力学模型的。
同样的,可以发现均质射流的涡环在活塞停止运动以后其冲量就几乎不发生变化了。而与之对应的,通过图10(b)~(d)可以观察到浮力涡环的冲量在一直下降,且随着Ri减小在其变化的速率越大,冲量变化的趋势是与环量变化趋势一致的。而在图10(d)中,冲量在t* = 5.5左右开始出现不变的情况,通过对比图8(d)可以发现,这种现象的出现也是由于涡环消散,涡环半径发生变化引起的。
同样的,先对涡核位置在 方向随时间变化的离散点进行拟合,然后取微分,就可以得出其运动速度Vx。再将环量、半径带入速度公式中(6),其中无量纲涡核半径采用Mohseni等 [23] 在1998实验测得的无量纲涡核半径ε = 0.3,求得Vc,在对速度无量纲化,得到无量纲的速度V1、V2如图11、图12所示,发现运动速度也是基本与细核涡环模型相符合。
 (a) Ri = 0
(a) Ri = 0 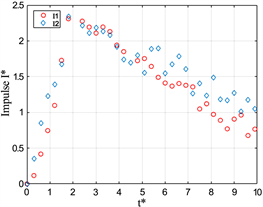 (b) Ri = −0.05
(b) Ri = −0.05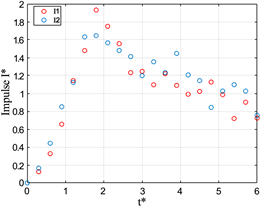 (c) Ri = −0.1
(c) Ri = −0.1 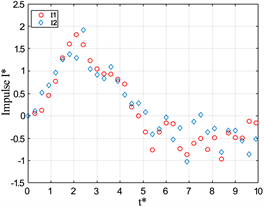 (d) Ri = −0.3
(d) Ri = −0.3
Figure 10. Dimensional impulse I* versus formation time t* at L/D = 2
图10. L/D = 2时,I*随t*变化的情况
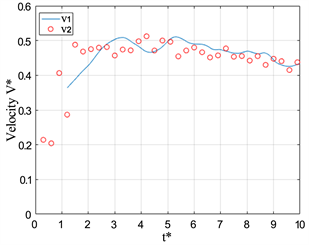
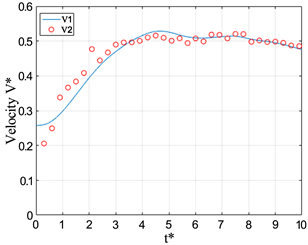
在两幅图中,在有浮力的条件下,都可以看到涡环都经历了加速到匀速到减速的过程。相对于均质射流产生的涡环速度,可以发现浮力涡环达到匀速运动的时间明显提前了,这也是浮力对涡环速度的一个重要影响。将图11与图12在相同Ri情况下对比,活塞运动的长度对浮力涡环达到匀速的时间并无较大的影响,但对涡环在匀速到减速这一时段内的影响比较大。通过对比图11(d)与图12(d),可以发现涡环的匀速过程在L/D = 3条件下增长了。
 (a) Ri = 0
(a) Ri = 0 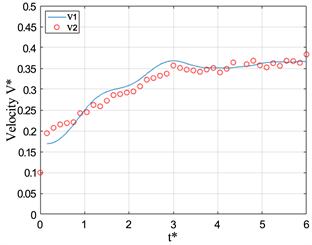 (b) Ri = −0.05
(b) Ri = −0.05 (c) Ri = −0.1
(c) Ri = −0.1 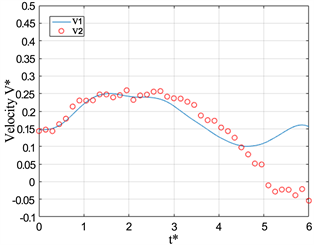 (d) Ri = −0.3
(d) Ri = −0.3
Figure 11. Dimensional Velocity V* versus formation time t* at L/D = 2
图11. L/D = 2时,V*随t*变化的情况
通过图12(a),可以发现均质射流的涡环速度V*在t* = 4以后都不发生变化了,保持在V* = 0.5左右,这表明涡环的运动速度约为活塞运行速度的二分之一,这一结果与之前关于均质射流产生的涡环的运动速度的研究结果吻合。而在有浮力的情况下,涡环也有一段匀速运动的过程,但其运动速度并不是一个不变的稳定值,在V* = 0.25~0.4区间,但还是小于均质射流的0.5,故而,负浮力也减小了涡环的传输速度。在图11(d)中,发现对通过位置随时间变化曲线求得的速度在t* = 4.8时刻后还上升,其主要原因是,在该时刻涡环已经开始消散,其涡核位置并不稳定所以出现了上述情况。
 (a) Ri = 0
(a) Ri = 0 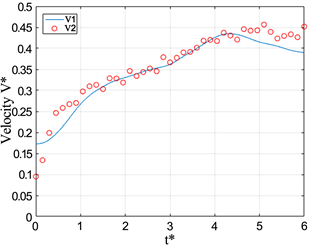 (b) Ri = −0.05
(b) Ri = −0.05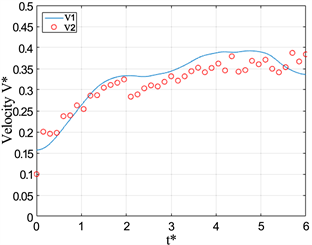 (c) Ri = −0.1
(c) Ri = −0.1 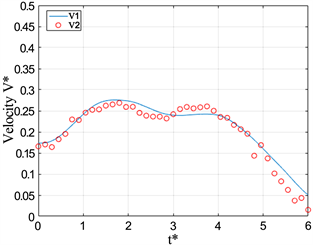 (d) Ri = −0.3
(d) Ri = −0.3
Figure 12. Dimensional Velocity V* versus formation time t* at L/D = 3
图12. L/D = 3时,V*随t*变化的情况
4. 结语
通过对L/D = 2、3的浮力涡环在不同理查德森数Ri情况下形成与演化的实验研究。通过涡量等值线、速度矢量图、涡核位置和涡环半径变化的分析,发现浮力在生成涡环过程中增加了涡环半径,减小了涡环的运动速度。还直观和间接地通过实验所得数据观测到了涡环在小Ri下的消散过程。通过对环量的分析,在L/D = 2的情况下,浮力在涡环生长过程中对涡环环量变化的影响较小,但在L/D = 3的情况下,当
以后,不同的Ri对涡环环量变化的影响开始增大。同时发现,随着理查德森数减小,在活塞停止后,涡环环量减小的速率与之成正相关。最后还对比了细核涡环的理论公式求得与实验得到的速度与水力冲量,可以推断浮力涡环属于细核涡环的范畴,也发现了浮力对涡环速度变化过程的影响。
参考文献
NOTES
*通讯作者。