1. 引言
近年来,随着仿生推进方式逐渐进入到人们的视野中,人们发现除了鱼的游动与昆虫及鸟类等动物的飞行方式外,以水母、乌贼和樽海鞘等生物为代表的非定常脉冲射流也是一种效率较高的推进方式。脉冲射流是通过间歇性和周期性地向周围环境流场喷射流体的一种推进方式。起动射流可以看作是脉冲射流的基本组成单元,它是指流体从静止状态加速通过喷管喷出,并逐渐达到稳态射流的过程。射流推进过程中,由于流体的粘性作用会在喷管壁面附近形成剪切层,剪切层在喷管出口发生卷曲作用,从而形成涡环。Gharib [1] 等人认为涡环的生长及发展揭示了非定常运动的效率最优规律。因此,涡环的形成是研究起动射流推进性能的一个重要因素,而影响涡环物理特征的参数主要是活塞的冲程比L/D,也称为涡环的形成时间(其中L是活塞移动的距离,D是活塞直径) [2] 。Gharib [1] 等人将形成时间定义为
,其中
为活塞推进平均速度。他们发现,在形成时间达到某个值后,前导涡环开始与尾迹
射流分离,逐渐发展到涡环本身不再卷吸周围流体,这一过程称为涡环夹止(Vortex ring pinch-off)。利用Kelvin-Benjamin变分原理中能量极值原理对这一现象进行解释,Gharib [1] 认为涡环的能量存在极限,并把涡环发生夹止对应的形成时间称为最佳形成时间。通过实验研究发现,最佳形成时间下涡环所产生的无量纲平均推力最大 [3] ,从力学的角度将涡环生长与起动射流推力特性联系在一起。
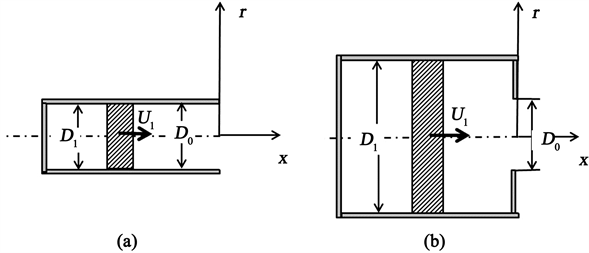
Figure 1. Schematic of (a) tube nozzle and (b) orifice type piston-cylinder vortex ring generations
图1. 起动射流产生装置示意图(a)圆管喷管(b)圆孔喷管
在起动射流的相关研究中,实验和模拟的推进器装置主要是活塞圆管喷管。而产生轴对称涡环的射流发生装置还有很多,其中主要的两种:一种是上述所说的圆管喷管,它是由喷管活塞推动流体,使其在圆筒形喷管出口产生射流起动涡环;另一种是由容器内活塞推动流体,流体从出口平面中间的圆孔处喷射出,从而产生圆孔起动涡环,即圆孔喷管,如图1所示。起动射流的发生装置出口形状差异对涡环形态及演化有很大的影响 [4] - [8] 。Pullin [4] 讨论了轴对称的圆管与圆孔出口几何形状对涡环形成的影响,基于相似理论的分析建立了涡环环量与涡核运动的理论模型。由于起动射流的出口超压效应能够加速涡环对周围流体的卷吸,有效的增强起动射流的推力性能 [5] 。因此考虑不同出口形状对超压效应的影响,Krueger [6] [7] [8] 从理论上研究了圆管和圆孔装置的射流环量,发现由于圆孔出口对流体的收缩作用,圆孔装置产生的射流环量明显大于圆管装置。
综上所述,虽然涡环特征影响的理论分析及数值模拟日趋完善,但是有关圆孔装置的研究还十分有限,而且极少从推进特性角度分析射流装置出口形状对涡环动力学特征的影响。因此,本文将主要从环量和冲量两个方面,讨论喷管直径比的变化对起动射流及其尾迹运动学和动力学特性的影响。
2. 数值模拟方法及验证
2.1. 计算方法及边界条件
因为涡环结构具有轴对称性且本文所有研究的介质为水,所以根据非定常不可压缩的轴对称N-S方程,利用有限体积法对控制方程进行离散。采用ANSYS FLUENT软件对流动进行数值分析,运用结构网格模拟涡环的演化和传输过程。通过MATLAB对数据后处理并提取不同时间的流场信息进行分析。采用与Krueger [7] [8] 相似的尺寸设定以消除边界对计算结果的影响,计算域及边界条件的设置如图2所示。由于涡环的对称性,模拟域为喷管的一半,喷管出口直径D0 = 0.02 m,计算域长度为20 D0,高度为3.5 D0。为了研究射流发生装置的出口几何形状变化对起动射流的影响,设定喷管长度为5 D0,入口尺寸为 。计算域中圆管和圆孔壁面均设定为无厚度虚拟壁面,且满足无滑移条件,区域远场边界均为压力出口,入口速度U1采用自定义函数的方式。区域下边界设置为对称轴。
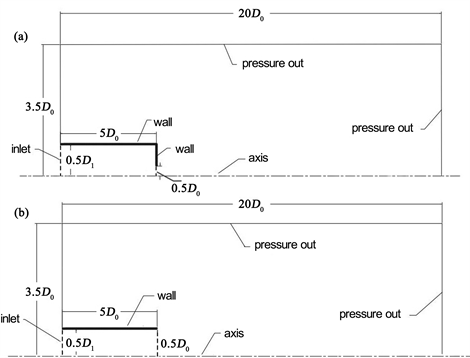
Figure 2. Domains and condition used in numerical simulation of vortex ring formation: (a) Tube nozzle; (b) Orifice nozzle. Note that the sketches are not drawn in proportion
图2. 数值模拟起动射流装置简图(a)圆管喷管;(b)圆孔喷管,示意图未按照比例绘制
本文为了研究出口形状变化对射流推力特性的影响,尽量减少由于速度差异造成的偏差,因此保证不同装置的射流出口速度函数U0一致,如图3所示。其中横坐标为物理时间,通过射流总时间T = 1.1 s进行无量纲化,纵坐标则通过出口最大速度U0max = 0.1 m/s对速度进行无量纲化。射流从入口速度U1 = 0.1开始运动,在T = 1.1 s的时候,射流运动停止。由于出口直径D0为定值,通过改变入口直径D1来改变装置形状,因此入口速度函数为
。根据冲程比公式可以计算,对于所研究的工况均有
。射流的出口雷诺数为
。本文将圆管和圆孔喷管的入口直径D1与出口直径D0的比值作为研究的变量,即直径比Dr。模拟总共研究了七种不同出口形状的工况,其直径比分别为Dr = 1、1.2、1.5、2、2.5、3以及4。

Figure 3. Exit velocity programs used to generate the starting jets
图3. 起动射流出口速度函数曲线
2.2. 数值结果验证
通过网格最优化处理,对网格无关性及时间步长独立性进行了分析,最终确定所研究的流场区域横纵坐标网格点分布分别为400 × 200,整个区域共有78,406个网格,且都采取LINE的分布规律对圆孔出口网格进行加密,最小网格尺寸为0.04 mm2,时间步长为1 ms。由于圆孔喷管实验结果很少,因此采用Gharib等人 [1] 对圆管喷管的实验条件及结果数据验证本文数值模拟的准确性,圆管出口直径为D0 = 1.63 cm,入口运动速度随时间的变化而恒定不变,速度为U1 = 7.5 cm/s。当速度达到规定时间t = 1.3 s后,速度变为0,产生的涡环继续演化传播。图4将涡环环量通过
进行无量纲化的结果与Gharib是实验数值对比,横坐标
为无量纲形成时间。可见,两者的误差小于5%,在可接受范围以内。
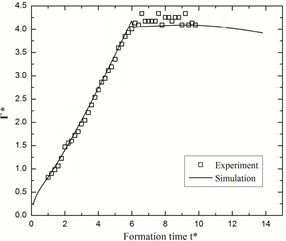
Figure 4. Comparison of the total circulation of the numerical and experimental results
图4. 无量纲环量的实验值与模拟值对比图
3. 结果及讨论
3.1. 起动射流动力学特征参数的变化
涡环的动力学参数主要有环量,冲量和能量,本文描述涡环动力特征主要围绕与射流推进特性相关的环量和冲量进行讨论。由于模拟软件FLUENT导出的数据均为不同时刻的离散变量,因此结合相关计算公式,采用数值积分以及插值法对数据进行后处理。参考Gharib [1] 的公式计算水力冲量和总环量分别为:
(1)
(2)
其中
是涡量在空间的分布。计算得到不同圆孔喷管直径比的起动射流动力学分析如下。对Dr = 1、1.2、1.5、2、2.5、3和4进行分析,其中Dr = 1即为圆管装置。参考相关文献 [1] ,利用出口最大速度U0max和出口直径 对环量无量纲化
,横坐标为无量纲形成时间。由于圆孔喷管所产生的起动射流总环量变化趋势相同,因此取Dr = 1和Dr = 2.5分别代表圆管和圆孔喷管,得到相应的起动射流总环量及水力冲量的变化如图5。从图5可以发现,两种喷管的环量变化趋势类似。在射流起动加速阶段,受到加速度的影响,环量快速上升,随后在匀速阶段,环量呈线性增长状态。在
时,射流运动减速停止,减速度使出口壁面剪切层产生反方向的速度梯度,从而形成负涡量涡环,即为滞止涡环。这种涡环的负涡量对环量具有抵消作用。射流的减速度和滞止涡环的共同作用使环量停止增长并且迅速下降 [9] 。随后环量在一个短时间内接近稳定,涡环向下游传输过程中,涡量受流体粘性的影响有一定的耗散,造成环量在较大的形成时间后缓慢下降。我们还参考了在涡环环量预测中,最常用的一维Slug模型,如公式(3)。
(3)
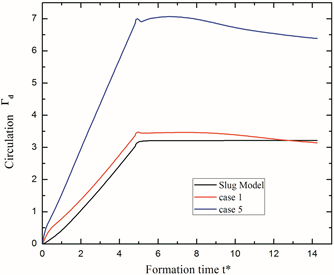
Figure 5. Evolution of dimensionless total circulation with Dr = 1 (case 1) and Dr = 2.5 (case 5)
图5. Dr = 1和2.5的喷管装置产生的起动射流环量的变化
(4)
而射流环量变化率的通用计算公式为公式(4) [10] ,由此可以发现Slug模型忽略了射流起动阶段出口径向速度的影响,也就忽略了出口超压这一因素,因此模型结果要小于圆管和圆孔喷管的模拟结果。尤其是圆孔装置,由于出口形状对射流的收缩作用在整个射流过程中一直存在,因此出口径向速度及出口超压效应一直较为明显,导致圆孔装置的环量要远大于圆管装置。这一结果也符合Krieg和Mohseni [10] 的研究,但是其研究的工况是控制圆管及圆孔喷管的入口速度函数U1相同,因此圆孔装置环量大幅度增加的一大部分原因是,出口对流体的收缩作用引起流体出口流速要大于圆管装置。而本文控制喷管出口速度函数U0相同,因此圆孔环量的增大更多的来自于出口超压效应的影响。压力效应的变化将在下一小节详细说明。
Dr = 1和2.5的另一个动力特征参数,水力冲量的分析如图6所示。图中对水力冲量进行了无量纲化,即
。与环量在加速阶段的发展相似,射流的水力冲量由于射流加速度的作用,在运动初期会有小幅度的陡升,然后线性上升直至射流减速阶段。当达到t* = 5左右时,起动射流开始减速至停止,射流减速作用使冲量陡降较小幅度。然后,随着无量纲形成时间的增加,水力冲量以很小的幅度上升。在大冲程比的情况下(本文冲程比
),圆管喷管的出口过压所产生的冲量只在射流加速阶段较为明显,而在匀速阶段,超压效应几乎可以忽略 [3] [10] ,因此对于圆管来说,Slug模型虽然忽略了出口过压所产生的冲量值,但是仍然能够很好的描述水力冲量。但是对于圆孔装置而言,射流出口收缩效应导致出口过压产生的额外冲量一直存在,因此Slug模型忽略压力效应造成的冲量误差也就更大,不能很好的描述圆孔装置环量和水力冲量的发展。这一结果也与Krieg和Mohseni [10] 的研究相符。
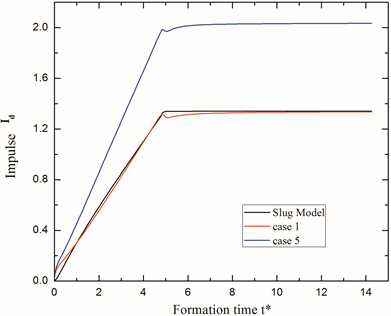
Figure 6. Evolution of dimensionless hydrodynamic impulse with Dr = 1 (case 1) and Dr = 2.5 (case 5)
图6. Dr = 1和2.5的喷管装置产生起动射流的水力冲量随时间的变化
为了研究不同起动射流出口形状变化对其推力特性的影响,选取涡环完全发展以后的环量和水力冲量作为代表值,即形成时间
时的环量和水力冲量值,绘制不同直径比下无量纲环量和水力冲量的变化曲线如图7。从图中黑色实心圆圈曲线可以观察到,随着直径比Dr的增加,圆孔出口对流体的收缩效应越加明显,从直径比Dr = 1到Dr = 2.5,环量增加了近两倍。但是,当直径比超过2.5以后,环量的增长率开始减小,Dr = 2.5到Dr = 4,环量值仅增加了2.24%。也就是说,当直径比达到某一值后,环量的增长幅度逐渐降低直至小于3%,环量随时间的变化趋于稳定。圆管和圆孔喷管的水力冲量也有相似的变化趋势,直径比Dr = 1升至Dr = 2.5,水力冲量有明显上升,且增长率高达约50%。然而,当直径比增加至Dr = 2.5后,水力冲量变化不明显。直径比从Dr = 2.5发展到4时,其水力冲量仅增长1.96%。

Figure 7. Evolution of dimensionless total circulation and hydrodynamic impulse with different diameter ratios
图7. 不同直径比的喷管装置产生的起动射流环量及冲量随直径比的变化
综上所述,直径比RD增加到一定值时,其对环量和水力冲量的影响几乎可以忽略。也就是说,当直径比增加到某一个临界值以后,喷管出口形状的变化对起动射流的推进特性没有明显的影响。Krueger [8] 在构建圆孔装置环量模型的时候提到,当Dr = 2的时候,模型能够更好的描述射流的环量。但是本文发现,在直径比从2增至2.5期间,水力冲量还是有2%左右的上升。而2.5以后,不同直径比装置产生的水力冲量的增长率在2%以下,可以忽略。
3.2. 出口超压效应对射流的影响
由于水力冲量和推力对起动射流的推进性能联系更加密切,因此为了研究上述与推力产生相关的动力学参数变化的原因,本节主要围绕水力冲量的组成成份进行分析。起动射流输送到下游涡环中的水力冲量Ih主要由两部分组成,流体动量变化量Iu和出口过压产生的冲量Ip [11] ,即:
(5)
其中
(6)
(6)
根据上述公式,影响起动射流水力冲量的因素主要从两个方面考虑,速度动量变化量IU和压力动量Ip。如图8选取直径比Dr = 1和2.5的工况分别代表圆管和圆孔喷管,进一步分析射流下游总冲量Ih的组成成分变化。其中方块及三角形标志的曲线分别代表通过上述公式计算得到的Dr = 1和2.5的水力冲量Ih,而黑色虚线及实线分别代表通过数值模拟计算得到的圆管及圆孔装置水力冲量值Im。从图中发现针对圆管和圆管喷管,都有出口压力冲量Ip0与出口动量变化量IU0之和等于流场总水力冲量Ih,而且对于圆孔装置,出口压力产生的额外冲量Ip0所占总冲量的比例很大,约为40%,这一结果与Krueger [3] [6] 结论相符。而圆管装置的出口压力冲量仅在射流加速阶段会有明显的升高,在射流匀速运动阶段,出口过压很小,相应的压力冲量趋近零值。

Figure 8. The comparison between pressure impulse and momentum flux of exit and total hydrodynamic impulse
图8. 起动射流出口过压冲量、出口动量变量和出口总冲量的对比
为了深入研究出口压力对总冲量的贡献程度,图9绘制了不同直径比下无量纲出口压力冲量随无量纲形成时间的变化。其中出口压力冲量的无量纲计算与前文冲量的无量纲计算公式相同。从图中可以发现,圆孔的出口过压形成的额外冲量远远大于圆管装置,这也是图6中,圆孔装置总冲量远远大于圆管装置的原因。图9中还对比了不同直径比的工况下,出口压力所产生的冲量占总冲量的比值变化。对圆孔装置而言,出口过压对其起动射流推力特性的影响更加明显,占比更大。而且随着直径比的增加,圆孔装置出口收缩效应更加明显,因此产生更大的出口压力冲量,其占总冲量的比值也逐渐升高,最终高达40%。当直径比达到2.5的时候,总冲量的增长趋势减慢,最终趋于稳定,直径比Dr = 4对应的出口压力冲量相比Dr = 2.5的情况仅增加了1.62%。
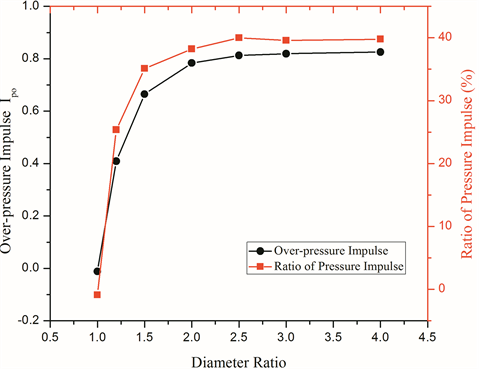
Figure 9. The pressure impulse and the ratio of the pressure impulse to the hydrodynamic impulse for starting jets with different diameter ratios
图9. 不同直径比工况下起动射流出口压力冲量的变化及其占总冲量的比值
由此可得,喷管产生的起动射流总冲量Ih主要受出口动量变化IU0及出口过压冲量Ip0的影响。由于本文控制圆管和圆孔喷管的出口速度函数相同,因此,两种装置的出口动量变化量相差不明显。影响起动射流总冲量Ih的主要因素为出口过压所产生的额外冲量Ip0,对于圆孔装置,Ip0至少占总冲量Ih的25%左右,且随直径比的增加,所占比更为显著,直到直径比为4时,占比高达40%左右。因此装置出口形状差异所引起的射流总冲量变化的规律,其实主要是出口形状对喷管出口压力冲量的影响。由于直径比增加,圆孔喷管的出口收缩作用增强,造成较大的出口压力。但是,当直径比达到2.5时,圆孔出口形状对流体的收缩作用趋于极限,出口压力冲量达到最大值,则总冲量也达到最大值,而后直径比的增加对起动射流冲量的影响几乎可以忽略。
3.3. 起动射流的推力冲量变化
上述分析主要集中于起动射流所形成的涡环动力学参数,对射流装置本身而言,影响其性能分析最为主要的参数则是射流装置所受到的推力FT。为了说明起动射流对装置推力性能的影响,我们对喷管的推力进行分析。起动射流作用在圆孔喷管上的推力FT可以通过下式计算,
(8)
其中Fpi为喷管入口压力,Fmi为入口速度动量变化率,Fpwi和Fpwo分别为圆孔出口平面内壁和外壁所受的压
力,对于圆管装置而言,Fpwi和Fpwo均为0。参考相关文献 [3] 对推力冲量无量纲化
,
则有不同直径比的射流装置的Fd变化如图10。图10(a)表示为起动射流整个过程中,装置所受推力的变化情况。在射流刚启动阶段加速度很大,因此装置所受推力作用突然增大,曲线呈陡升趋势;在匀速阶段,加速度减为零,喷管不再受推力作用,射流推进装置的推力主要由喷射流体的动量变化来提供。当射流减速时,推力向反方向作用,因此Fd开始变为负值,最终射流停止,推力逐渐趋于零。从图10(a)可以发现,推进装置所受推力的主要差异在于匀速阶段,因此对匀速阶段放大分析得到图10(b)。圆孔产生的起动射流推力均大于圆管喷管。这是由于装置形状的影响导致圆孔装置的出口压力作用较圆管大很多,压差造成的额外推力使圆孔装置所受推力大于圆管装置,而且随直径比增加,出口压力占比增大,推力也随之增加。与总冲量的变化相似,当直径比增加到2.5的时候,射流装置所受推力FT达到最大值。即使直径比继续增加,FT的增长率一直低于2%。
 (a)
(a)  (b)
(b)
Figure 10. Evolution of net propulsive thrust of starting jet in (a) the whole jet phase (b) the uniform velocity phase for different diameter ratio
图10. 不同直径比的射流装置所受推力(a)在射流运动过程中(b)在射流匀速运动阶段的变化
起动射流对推进器的推力作用也受到喷管出口形状的影响。基于出口超压效应的影响,圆孔喷管所受推力相比圆管喷管更强。也就是说,在保证出口流量相同的情况下,圆孔形状能够对推进器施加更强的推力。而且随着直径比的增强,推力也逐渐增大,直到推进器入口与出口直径比约为2.5时,推力达到最大值,此时改变出口形状,对推力特性的影响很小。
4. 总结
非定常起动射流相比稳态射流存在更高的推进效率,而与其效率最优化密切相关的流动特征即为射流所产生的涡环。本文以喷管的直径比为参数,研究不同出口形状对推进装置推进特性的影响。将推进喷管的入口与出口直径比Dr作为变量,通过改变入口直径来改变Dr,从而定义了不同的喷管形状。利用数值模拟方法,研究了射流环量Г和水力冲量Ih的变化,结果发现圆孔喷管的Г和Ih都明显大于圆管装置。结合水力冲量的组成成分分析发现,这是由于在射流喷射过程中,圆孔喷管出口处的垂直壁面对流体产生一定的收缩作用,从而形成持续的超压效应,如图9,随着直径比的增加,出口超压产生的额外冲量Ipo也一直增加,直到Dr > 2.5,压力冲量仅增长了1.62%。超压效应产生的额外冲量Ipo占总冲量Ih的比例最高约为40%,因此Ih的发展受Ipo的影响很大。其增长趋势随着直径比的增加而减弱,当直径比Dr = 2.5时,Ih几乎达到最大值,即直径比由2.5增加到4时,Ih仅增加了1.96%。
由于推力是衡量推进器性能的重要指标,对射流所形成的推力 也进行了研究。与水力冲量Ih变化相似,当直径比达到某个极限值,即2.5时,FT的变化趋于稳定,即使直径比继续增加,FT的增长率也小于2%。总之,通过上述模拟结果及相关分析,可以发现推进器出口形状的变化对起动射流的推进性能存在较大的影响,本文结论为水下推进器的出口设计及参数选取提供了理论参考,而直径比与动力特征参数之间具体定量关系式仍然值得进一步研究。
NOTES
*通讯作者。