特殊矩阵行列式的计算

Computation of the Determinants of Special Matrices

摘要: 矩阵和行列式在科学与工程中经常遇到。矩阵的特征多项式、特征值都需要计算其行列式。本文针对一些特殊矩阵，讨论其行列式的计算问题，包括特殊矩阵的特征多项式的计算。

Abstract: Matrix and determinant are often encountered in science and engineering. The characteristic polynomial and eigenvalues of a matrix require computing its determinant. Aiming at some special matrices, this paper discusses the calculation problems of some determinants, including the characteristic polynomials of some special matrices.

1. 引言

矩阵、行列式、特征值、特征多项式是线性代数和矩阵论中的基本内容。矩阵特征多项式与特征值的计算与矩阵的行列式密切相关。友矩阵是一类特殊矩阵，在现代控制理论中经常用到，友矩阵中的非零元与其特征值多项式的系数有一一对应关系。友矩阵有四种基本类型，最近文献 [1] 讨论了友矩阵间的变换关系，文献 [2] 研究了特殊矩阵的矩阵指数的计算方法。严坤妹讨论了一类矩阵特征值多项式的计算问题 [3] 。冯纯伯研究了矩阵多项式特征值的计算 [4] 。

本文章侧重于讨论特殊矩阵的行列式计算以及特殊矩阵的特征多项式的求法。使用不同技巧和方法，从不同的角度进行分析，合理地利用行列式的运算性质以及特殊的求解方法，比如归纳法等，从而对一些特殊的行列式的求解方法进行探究与比较，还包含从求解方法当中提炼出来的引申与思考。

2. 计算友矩阵特征多项式和行列式

在现代控制理论中，友矩阵(companion matrix)在传递函数的状态空间规范型实现中非常有用，其特征多项式的计算非常重要。友矩阵有四种形式。n阶友矩阵具有下列形式：

$A_n=\left(\begin{array}{ccccc}-a_1& -a_2& \cdots & -a_{n-1}& -a_n\\ 1& 0& \cdots & 0& 0\\ 0& 1& \cdots & 0& 0\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ 0& 0& \dots & 1& 0\end{array}\right)$ ，

它的转置矩阵也是友矩阵，沿斜对角线转置矩阵也是友矩阵。这四个友矩阵具有相同的特征值多项式。

设 $I_n$ 是n阶单位阵。友矩阵的特征值多项式

$f_n\left(s\right):=\left|s{I}_n-A_n\right|=\left|\begin{array}{ccccc}s+a_1& a_2& \cdots & a_{n-1}& a_n\\ -1& s& \cdots & 0& 0\\ 0& -1& \cdots & 0& 0\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ 0& 0& \cdots & -1& s\end{array}\right|$

展开之后得到关于s的n次多项式。采用归纳法，先计算 $n=1$ 时的特征值多项式 $f_1\left(s\right)=s+a_1$ ；当 $n=2$ 时的特征值多项式为

$f_2\left(s\right)=\left|\begin{array}{cc}s+a_1& a_2\\ -1& s\end{array}\right|=s{f}_1\left(s\right)+a_2=s\left(s+a_1\right)+a_2$

展开时先从右下角的s开始展开，然后向左上方推移得到

$f_3\left(s\right)=\left|\begin{array}{ccc}s+a_1& a_2& a_3\\ -1& s& 0\\ 0& -1& s\end{array}\right|=s{f}_2\left(s\right)-\left(-1\right)\left|\begin{array}{cc}s+a_1& a_3\\ -1& 0\end{array}\right|=s{f}_2\left(s\right)+a_3$

$\begin{array}{c}{f}_4\left(s\right)=\left|\begin{array}{cccc}s+a_1& a_2& a_3& a_4\\ -1& s& 0& 0\\ 0& -1& s& 0\\ 0& 0& -1& s\end{array}\right|=s{f}_3\left(s\right)-\left(-1\right)\left|\begin{array}{ccc}s+a_1& a_2& a_4\\ -1& s& 0\\ 0& -1& 0\end{array}\right|\\ =s{f}_3\left(s\right)+\left|\begin{array}{cc}s+a_1& a_4\\ -1& 0\end{array}\right|=s{f}_3\left(s\right)+a_4\end{array}$

由此猜测： $f_5\left(s\right)=s{f}_4\left(s\right)+a_5,\cdots ,f_n\left(s\right)=s{f}_{n-1}\left(s\right)+a_n$ ，代入化简得到

$\begin{array}{l}{f}_1\left(s\right)=s+a_1\\ f_2\left(s\right)=s\left(s+a_1\right)+a_2=s^2+s{a}_1+a_2\\ f_3\left(s\right)=s\left(s^2+s{a}_1+a_2\right)+a_3=s^3+s^2{a}_1+s{a}_2+a_3\\ f_4\left(s\right)=s\left(s^3+s^2{a}_1+s{a}_2+a_3\right)+a_4=s^4+s^3{a}_1+s^2{a}_2+s{a}_3+a_4\\ ⋮\\ f_n\left(s\right)=s^n+s^{n-1}{a}_1+s^{n-2}{a}_2+s^{n-3}{a}_3+\cdots +a_n=s^n+{\displaystyle \underset{i=1}{\overset{n}{\sum }}{s}^{n-i}{a}_i}\end{array}$

下面加以证明：当 $n=1$ 时， $f_1\left(s\right)=s+a_1$ ，

$\begin{array}{c}{f}_{n+1}\left(s\right)=s{f}_n\left(s\right)+\left(-1\right){\left(-1\right)}^{2n+1}\left|\begin{array}{cccccc}s+a_1& a_2& \cdots & a_{n-2}& a_{n-1}& a_{n+1}\\ -1& s& \cdots & 0& 0& 0\\ ⋮& ⋮& \ddots & ⋮& ⋮& ⋮\\ 0& 0& \cdots & -1& s& 0\\ 0& 0& \cdots & 0& -1& 0\end{array}\right|\\ =s{f}_n\left(s\right)+\left(-1\right){\left(-1\right)}^{2n-1}\left|\begin{array}{cccccc}s+a_1& a_2& \cdots & a_{n-3}& a_{n-2}& a_{n+1}\\ -1& s& \cdots & 0& 0& 0\\ ⋮& ⋮& \ddots & ⋮& ⋮& ⋮\\ 0& 0& \cdots & -1& s& 0\\ 0& 0& \cdots & 0& -1& 0\end{array}\right|\end{array}$

由于每一个行列式中元素−1所在位置的行数与列数之和为奇数，且该行其他元素的值均为0，因此只需要一步步地去算它的代数余子式即可。最后

$\begin{array}{c}{f}_{n+1}\left(s\right)=s{f}_n\left(s\right)+\left|\begin{array}{cc}s+a_1& a_{n+1}\\ -1& 0\end{array}\right|=s{f}_n\left(s\right)+a_{n+1}\\ =s\left(s^n+{\displaystyle \underset{i=1}{\overset{n}{\sum }}{a}_i{s}^{n-i}}\right)+a_{n+1}=s^{n+1}+{\displaystyle \underset{i=1}{\overset{n+1}{\sum }}{a}_i{s}^{n+1-i}}\end{array}$

得证。

归纳有从k到 $k+1$ 的归纳，有时还需要隔项进行归纳，比如从k到 $k+2$ 进行归纳。这时往往需要进行奇偶分析，因为奇数和偶数在化简时可能出现不同的递推公式。下面的两个例子，都是从k到 $k+2$ 项进行归纳。

3. 计算十字叉形壹矩阵的特征多项式

n阶十字叉形壹矩阵具有下列形式：

$A_n={\left(\begin{array}{ccccc}1& & & & 1\\ & 1& & 1& \\ & & \ddots & & \\ & 1& & 1& \\ 1& & & & 1\end{array}\right)}_{n\times n}$ (未写出部分的值均为0)，

$A_n$ 的特征多项式为

$f_n\left(s\right)=\left|s{I}_n-A_n\right|=\left|\begin{array}{ccccc}s-1& & & & -1\\ & s-1& & -1& \\ & & \ddots & & \\ & -1& & s-1& \\ -1& & & & s-1\end{array}\right|$

其中 $f_1\left(s\right)=s-1$ ， $f_2\left(s\right)=\left|\begin{array}{cc}s-1& -1\\ -1& s-1\end{array}\right|={\left(s-1\right)}^2-1=s^2-2s$ 。

此行列式 $f_n\left(s\right)$ 的对称性比较好，应该首先寻找关于 $f_n\left(s\right)$ 的递推公式。由于此n阶行列式和居中的 $n-2$ 阶行列式的结构非常相似，所以更倾向于去寻找 $f_n\left(s\right)$ 与 $f_{n-2}\left(s\right)$ 的递推关系。因为 $f_1\left(s\right)$ 与 $f_2\left(s\right)$ 均为已知，这样就能够得到递推关系式。当n的奇偶性不同时，行列式最中心的结构不同，所以需要分奇偶进行讨论。

① 当n为奇数时，

$\begin{array}{c}{f}_n\left(s\right)=\left(s-1\right)\left|\begin{array}{cccc}s-1& \cdots & -1& 0\\ ⋮& \ddots & ⋮& ⋮\\ -1& \cdots & s-1& 0\\ 0& \cdots & 0& s-1\end{array}\right|+\left(-1\right)\left|\begin{array}{cccc}0& \cdots & 0& -1\\ s-1& \cdots & -1& 0\\ ⋮& \ddots & ⋮& ⋮\\ -1& \cdots & s-1& 0\end{array}\right|\\ ={\left(s-1\right)}^2{f}_{n-2}\left(s\right)+\left(-1\right)\left(-1\right){\left(-1\right)}^n{f}_{n-2}\left(s\right)\\ =\left(s^2-2s\right)f_{n-2}(s)\end{array}$

② 当n为偶数时，

$\begin{array}{c}{f}_n\left(s\right)=\left(s-1\right)\left|\begin{array}{cccc}s-1& \cdots & -1& 0\\ ⋮& \ddots & ⋮& ⋮\\ -1& \cdots & s-1& 0\\ 0& \cdots & 0& s-1\end{array}\right|-\left(-1\right)\left|\begin{array}{cccc}0& \cdots & 0& -1\\ s-1& \cdots & -1& 0\\ ⋮& \ddots & ⋮& ⋮\\ -1& \cdots & s-1& 0\end{array}\right|\\ ={\left(s-1\right)}^2{f}_{n-2}\left(s\right)-\left(-1\right)\left(-1\right){\left(-1\right)}^n{f}_{n-2}\left(s\right)\\ =\left(s^2-2s\right)f_{n-2}(s)\end{array}$

所以当 $n\ge 3$ 时，有 $f_n\left(s\right)=\left(s^2-2s\right)f_{n-2}\left(s\right)$ ，又因为 $f_1\left(s\right)=s-1$ ， $f_2\left(s\right)=s^2-2s$ ，所以当n为奇数时， $f_n\left(s\right)=\left(s-1\right){\left(s^2-2s\right)}^{\frac{n-1}{2}}$ ；当n为偶数时， $f_n\left(s\right)={\left(s^2-2s\right)}^{\frac{n}{2}}$ 。所以

$f_n\left(s\right)=\{\begin{array}{l}\left(s-1\right){\left(s^2-2s\right)}^{\frac{n-1}{2}},n为奇数\\ {\left(s^2-2s\right)}^{\frac{n}{2}},n为偶数\end{array}$

对于呈中心对称型的行列式，也有其特殊的简化算法。

4. 计算块单位阵的特征值多项式

2n阶块单位阵 $A_{2n}={\left[\begin{array}{cc}{I}_n& I_n\\ I_n& I_n\end{array}\right]}_{2n\times 2n}$ 的特征多项式为

$f_{2n}\left(s\right):=\left|s{I}_{2n}-A_{2n}\right|=\left|\begin{array}{cccccc}s-1& & & -1& & \\ & \ddots & & & \ddots & \\ & & s-1& & & -1\\ -1& & & s-1& & \\ & \ddots & & & \ddots & \\ & & -1& & & s-1\end{array}\right|$

当 $n=1$ 时， $f_2\left(s\right)=\left|\begin{array}{cc}s-1& -1\\ -1& s-1\end{array}\right|=s\left(s-2\right)$ 。注意到此行列式为中心对称行列式，可以进行操作： $r_1+r_{2n}$ ， $r_2+r_{2n-1}$ ， $\cdots$ ， $r_n+r_{n+1}$ ( $r_i$ 表示第i行)，即把最后一行的值加到第1行上，把倒数第2行的值加到第2行上，依次类推，一直加到最中间的那两行。但此时也需要对n进行奇偶讨论。

① 当n为奇数时，

$f_{2n}\left(s\right)=\left|\begin{array}{cccccccccc}s-1& & & & -1& -1& & & & s-1\\ & \ddots & & ⋰& & & \ddots & & ⋰& \\ & & s-2& & & & & s-2& & \\ & ⋰& & \ddots & & & ⋰& & \ddots & \\ -1& & & & s-1& s-1& & & & -1\\ -1& & & & & s-1& & & & \\ & \ddots & & & & & \ddots & & & \\ & & -1& & & & & s-1& & \\ & & & \ddots & & & & & \ddots & \\ & & & & -1& & & & & s-1\end{array}\right|$

② 当n为偶数时，

$f_{2n}\left(s\right)=\left|\begin{array}{cccccccccccc}s-1& & & & & -1& -1& & & & & s-1\\ & \ddots & & & ⋰& & & \ddots & & & ⋰& \\ & & s-1& -1& & & & & -1& s-1& & \\ & & -1& s-1& & & & & s-1& -1& & \\ & ⋰& & & \ddots & & & ⋰& & & \ddots & \\ -1& & & & & s-1& s-1& & & & & -1\\ & & -I_n& & & & & & \left(s-1\right)I_n& & & \end{array}\right|$

但无论n为奇数还是偶数，对于整个行列式的每一列的上半列来说，都有 $c_1=c_{2n}$ ， $c_2=c_{2n-1}$ ， $\cdots$ ， $c_n=c_{n+1}$ ( $c_i$ 表示第i列)。此时可对此行列式进行如下变换： $c_{2n}-c_1$ ， $c_{2n-1}-c_2$ ， $\cdots$ ， $c_{n+1}-c_n$ 。这样整个行列式右上角的所有元均为零了，然后再利用行列式的计算性质进行化简。

① 当n为奇数时，

$\begin{array}{c}{f}_{2n}\left(s\right)=\left|\begin{array}{cccccccccc}s-1& & & & -1& & & & & \\ & \ddots & & ⋰& & & & & & \\ & & s-2& & & & & 0& & \\ & ⋰& & \ddots & & & & & & \\ -1& & & & s-1& & & & & \\ -1& & & & & s-1& & & & 1\\ & \ddots & & & & & \ddots & & ⋰& \\ & & -1& & & & & s& & \\ & & & \ddots & & & ⋰& & \ddots & \\ & & & & -1& 1& & & & s-1\end{array}\right|\\ =\left|\begin{array}{ccccc}s-1& & & & -1\\ & \ddots & & ⋰& \\ & & s-2& & \\ & ⋰& & \ddots & \\ -1& & & & s-1\end{array}\right|\cdot \left|\begin{array}{ccccc}s-1& & & & 1\\ & \ddots & & ⋰& \\ & & s& & \\ & ⋰& & \ddots & \\ 1& & & & s-1\end{array}\right|\end{array}$

这时可以利用上一例题结论，分别去寻找这两个行列式的n阶与其对应的 $n-2$ 阶行列式的关系进行求解，最终发现，无论是左边还是右边的行列式，都满足关系式： $g_n\left(s\right)=\left(s^2-2s\right)g_{n-2}\left(s\right)$ 。这种方法和结论在n为偶数时同样也适用。所以当n为奇数时，有

$\begin{array}{c}{f}_n\left(s\right)=\left(s-2\right){\left(s^2-2s\right)}^{\frac{n-1}{2}}\cdot s{\left(s^2-2s\right)}^{\frac{n-1}{2}}\\ ={\left(s^2-2s\right)}^n\end{array}$

② 当n为偶数时，

$\begin{array}{c}{f}_{2n}\left(s\right)=\left|\begin{array}{cccccccccccc}s-1& & & & & -1& & & & & & \\ & \ddots & & & ⋰& & & & & & & \\ & & s-1& -1& & & & & \begin{array}{l}\\ 0\end{array}& & & \\ & & -1& s-1& & & & & & & & \\ & ⋰& & & \ddots & & & & & & & \\ -1& & & & & s-1& & & & & & \\ -1& & & & & & s-1& & & & & 1\\ & \ddots & & & & & & \ddots & & & ⋰& \\ & & -1& & & & & & s-1& 1& & \\ & & & -1& & & & & 1& s-1& & \\ & & & & \ddots & & & ⋰& & & \ddots & \\ & & & & & -1& 1& & & & & s-1\end{array}\right|\\ =\left|\begin{array}{cccccc}s-1& & & & & -1\\ & \ddots & & & ⋰& \\ & & s-1& -1& & \\ & & -1& s-1& & \\ & ⋰& & & \ddots & \\ -1& & & & & s-1\end{array}\right|\cdot \left|\begin{array}{cccccc}s-1& & & & & 1\\ & \ddots & & & ⋰& \\ & & s-1& 1& & \\ & & 1& s-1& & \\ & ⋰& & & \ddots & \\ 1& & & & & s-1\end{array}\right|\\ =\left(s^2-2s\right){\left(s^2-2s\right)}^{\frac{n-2}{2}}\cdot \left(s^2-2s\right){\left(s^2-2s\right)}^{\frac{n-2}{2}}\\ ={\left(s^2-2s\right)}^n\end{array}$

所以矩阵 $A$ 的特征值多项式为 $f_n\left(s\right)={\left(s^2-2s\right)}^n$ 。

以上是对归纳法的一些分析，下面是一些对不同型行列式计算的特殊方法的举例。

对于每一行(列)的和都相同的行列式，可以把每一行(列)的和全部都加到第一行(列)上，然后将这一行(列)的公因式进行提取，从而简化行列式的计算。

5. 计算壹矩阵的特征值多项式

n阶壹矩阵具有下列形式：

$A={\left(\begin{array}{ccccc}1& 1& \cdots & 1& 1\\ 1& 1& \cdots & 1& 1\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ 1& 1& \cdots & 1& 1\\ 1& 1& \cdots & 1& 1\end{array}\right)}_{n\times n}$

壹矩阵的特征多项式为

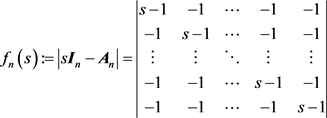
把每一列的值全部加到第1列上，即 $c_1+c_2$ ， $c_1+c_3$ ， $\cdots$ ， $c_1+c_n$ ：

$f_n\left(s\right)=\left|\begin{array}{ccccc}s-n& -1& \cdots & -1& -1\\ s-n& s-1& \cdots & -1& -1\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ s-n& -1& \cdots & s-1& -1\\ s-n& -1& \cdots & -1& s-1\end{array}\right|=\left(s-n\right)\cdot \left|\begin{array}{ccccc}1& -1& \cdots & -1& -1\\ 1& s-1& \cdots & -1& -1\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ 1& -1& \cdots & s-1& -1\\ 1& -1& \cdots & -1& s-1\end{array}\right|$

再把每1列加到其它列上，即 $c_2+c_1$ ， $c_3+c_1$ ， $\cdots$ ， $c_n+c_1$ ：

$f_n\left(s\right)=\left(s-n\right)\left|\begin{array}{ccccc}1& 0& \cdots & 0& 0\\ 1& s& \cdots & 0& 0\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ 1& 0& \cdots & s& 0\\ 1& 0& \cdots & 0& s\end{array}\right|=\left(s-n\right)s^{n-1}$

如果行列式的上三角和下三角的值不相同，那么这种方法就不适用了。对于这样的问题，需要先对行列式进行变形，然后才能利用原来的模型进行归纳或化简。

6. 计算斜对称矩阵的行列式

计算下列n阶斜对称矩阵的行列式( $b\ne c$ ) [5] ：

$A_n={\left|\begin{array}{ccccc}a& b& b& \cdots & b\\ c& a& b& \cdots & b\\ c& c& a& \cdots & b\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ c& c& c& \cdots & a\end{array}\right|}_{n\times n}$ ，

从第n行开始，将此行列式的每一行减去前一行，直到第一行，即 $r_n-r_{n-1}$ ， $r_{n-1}-r_{n-2}$ ， $\cdots$ ， $r_3-r_2$ ， $r_2-r_1$ ：

$\begin{array}{c}{A}_n=\left|\begin{array}{cccccc}a& b& b& \cdots & b& b\\ c& a& b& \cdots & b& b\\ c& c& a& \cdots & b& b\\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮\\ c& c& c& \cdots & a& b\\ c& c& c& \cdots & c& a\end{array}\right|\begin{array}{c}\underset{\_}{\underset{\_}{r}}\\ \end{array}\left|\begin{array}{cccccc}a& b& b& \cdots & b& b\\ c-a& a-b& 0& \cdots & 0& 0\\ 0& c-a& a-b& \cdots & 0& 0\\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮\\ 0& 0& 0& \cdots & a-b& 0\\ 0& 0& 0& \cdots & c-a& a-b\end{array}\right|\\ =a{\left(a-b\right)}^{n-1}+\left(a-c\right)\cdot b\left|\begin{array}{cccccc}1& 1& 1& \cdots & 1& 1\\ c-a& a-b& 0& \cdots & 0& 0\\ 0& c-a& a-b& \cdots & 0& 0\\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮\\ 0& 0& 0& \cdots & a-b& 0\\ 0& 0& 0& \cdots & c-a& a-b\end{array}\right|\end{array}$

令上述等式中的行列式的值为 $x_{n-1}$ ，代入上式于是有 $x_n=a{\left(a-b\right)}^{n-1}+b\left(a-c\right)x_{n-1}$ ，这样就把原来的问题转化为去求解一个新行列式的值的问题，与前面介绍的友矩阵的形式类似。

将此行列式按第一列进行展开，不难得到关于的递推公式

$x_{n-1}={\left(a-b\right)}^{n-2}+\left(a-c\right)x_{n-2}$

这样可以通过归纳来写出的表达式，进而求出 $x_n$ ，从而得到行列式的值。

$\begin{array}{l}{x}_1=1,\\ x_2=\left(a-b\right)+\left(a-c\right),\\ x_3={\left(a-b\right)}^2+\left(a-b\right)\left(a-c\right)+{\left(a-c\right)}^2,\\ x_4={\left(a-b\right)}^3+{\left(a-b\right)}^2\left(a-c\right)+\left(a-b\right){\left(a-c\right)}^2+{\left(a-c\right)}^3,\cdots \end{array}$

通过归纳，不难得到

$\begin{array}{c}{x}_{n-1}={\left(a-b\right)}^{n-2}+{\left(a-b\right)}^{n-3}\left(a-c\right)+\cdots +\left(a-b\right){\left(a-c\right)}^{n-3}+{\left(a-c\right)}^{n-2}\\ =\frac{{\left(a-b\right)}^{n-1}-{\left(a-c\right)}^{n-1}}{\left(a-b\right)-\left(a-c\right)}=\frac{{\left(a-b\right)}^{n-1}-{\left(a-c\right)}^{n-1}}{c-b}\end{array}$

即

$\begin{array}{c}{x}_n=a{\left(a-b\right)}^{n-1}+b\left(a-c\right)\cdot \frac{{\left(a-b\right)}^{n-1}-{\left(a-c\right)}^{n-1}}{c-b}\\ =\frac{a\left(c-b\right){\left(a-b\right)}^{n-1}+b\left(a-c\right){\left(a-b\right)}^{n-1}-b{\left(a-c\right)}^n}{c-b}\\ =\frac{c{\left(a-b\right)}^n-b{\left(a-c\right)}^n}{c-b}\end{array}$

7. 计算对称矩阵的行列式

1) 计算n阶行列式 [5] ：

$D_n=\left|\begin{array}{cccc}1+a_1& 1& \cdots & 1\\ 1& 1+a_2& \cdots & 1\\ ⋮& ⋮& \ddots & ⋮\\ 1& 1& \cdots & 1+a_n\end{array}\right|$ ，其中 $a_1{a}_2\cdots a_n\ne 0$ ；

2) $F_n=\left|\begin{array}{cccc}1+a_1& a_1& \cdots & a_1\\ a_2& 1+a_2& \cdots & a_2\\ ⋮& ⋮& \ddots & ⋮\\ a_n& a_n& \cdots & 1+a_n\end{array}\right|$ 。

行列式有一条加法的性质，即行列式的某一行是两组数的和，则这个行列式等于两个行列式的和。这两个行列式分别以其中某一组数作为该行，而其它行均与原行列式相同。如果用算式表达，即

$\left|\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ ⋮& ⋮& & ⋮\\ b_1+c_1& b_2+c_2& \cdots & b_n+c_n\\ ⋮& ⋮& & ⋮\\ a_{n1}& a_{n2}& \cdots & a_{nn}\end{array}\right|=\left|\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ ⋮& ⋮& & ⋮\\ b_1& b_2& \cdots & b_n\\ ⋮& ⋮& & ⋮\\ a_{n1}& a_{n2}& \cdots & a_{nn}\end{array}\right|+\left|\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ ⋮& ⋮& & ⋮\\ c_1& c_2& \cdots & c_n\\ ⋮& ⋮& & ⋮\\ a_{n1}& a_{n2}& \cdots & a_{nn}\end{array}\right|$

在解决问题时，很多行列式不只有一行的形式较为复杂，可以多次运用此公式来进行化简。如果行列式的每一行都有一些元素是多项之和时，那么此时可以用上述公式n次，让这个较复杂的行列式的每一行都利用上述公式进行展开。每利用公式展开一次，行列式的个数就会比原来多一倍。经过n次展开后，会得到 $2^n$ 个形式较为简单的子行列式。

对于(1)，不妨设 $A=\left(\begin{array}{cccc}1& 1& \cdots & 1\\ 1& 1& \cdots & 1\\ ⋮& ⋮& \ddots & ⋮\\ 1& 1& \cdots & 1\end{array}\right)$ ， $B=\left(\begin{array}{cccc}{a}_1& & & \\ & a_2& & \\ & & \ddots & \\ & & & a_n\end{array}\right)$ ，则 $D_n=\left|A+B\right|$ 。等价于求一个所有元素全是1的矩阵和一个对角阵的和矩阵的行列式。

如果从横向的角度去分析，从第一行开始拆成两个行列式，一直到最后一行，不仅工作量大，而且不好找出规律。因此我们可以从纵向的角度去分析，也就是从按照上述公式拆完之后的 $2^n$ 个行列式的性质进行分析。

也就是说从 $A$ 的第一列或者从 $B$ 的第一列当中任取一列，当做子行列式的第一列；从 $A$ 的第二列或者从 $B$ 的第二列当中任取一列，当做子行列式的第二列……一直到第n列为止。对于子行列式当中的每一列都有2种取法，所以最后会有 $2^n$ 种形式不同的子行列式，也刚好符合最初的判断。但对于这 $2^n$ 个子行列式，只要其中有大于等于两列来自于 $A$ 中，那么这个子行列式的值为零，剩下值不为零的子行列式要么只有一列来自 $A$ ，或者全来自于 $B$ 。从而使问题大大简化。因此有

$\begin{array}{c}{D}_n=\left(a_2{a}_3\cdots a_n+a_1{a}_3{a}_4\cdots a_n+a_1{a}_2{a}_4{a}_5\cdots a_n+\cdots +a_1{a}_2\cdots a_{n-1}\right)+a_1{a}_2\cdots a_n\\ =a_1{a}_2\cdots a_n\left(\frac{1}{a_1}+\frac{1}{a_2}+\cdots +\frac{1}{a_n}+1\right)\\ =a_1{a}_2\cdots a_n\left(1+{\displaystyle \underset{i=1}{\overset{n}{\sum }}\frac{1}{a_i}}\right)\end{array}$

基于上述分析与(1)的结果，问题(2)就易于求解了。不妨设

$A=\left(\begin{array}{cccc}1& & & \\ & 1& & \\ & & \ddots & \\ & & & 1\end{array}\right)$ ， $B=\left(\begin{array}{cccc}{a}_1& a{}_1& \cdots & a_1\\ a_2& a_2& \cdots & a_2\\ ⋮& ⋮& \ddots & ⋮\\ a_n& a_n& \cdots & a_n\end{array}\right)$ ，

则 $F_n=\left|A+B\right|$ 。同样对于展开之后的 $2^n$ 个子行列式来说，其中值不为零的行列式只包含两种情况：

① 子行列式中的每一列均来自于 $A$ ；

② 子行列式中有且只有一列来自于 $B$ 。

只有单位阵的行列式满足于第①种情况。现将第②种情况的子行列式的求法做一般项分析。假设子行列式中来自于 $B$ 的那一列是第i列，则

$\left|\begin{array}{cccccc}1& & & a_1& & \\ ⋮& 1& & a_2& & \\ ⋮& & \ddots & ⋮& & \\ 0& \cdots & \cdots & a_i& & \\ & & & ⋮& \ddots & \\ & & & a_n& & 1\end{array}\right|\begin{array}{c}\underset{\_}{\underset{\_}{c_1\leftrightarrow c_i}}\\ \end{array}-\left|\begin{array}{cccccc}{a}_1& & & 1& & \\ a_2& 1& & ⋮& & \\ ⋮& & \ddots & ⋮& & \\ a_i& \cdots & \cdots & 0& & \\ ⋮& & & & \ddots & \\ a_n& & & & & 1\end{array}\right|\begin{array}{c}\underset{\_}{\underset{\_}{r_1\leftrightarrow r_i}}\\ \end{array}\left|\begin{array}{cccccc}{a}_i& & & & & \\ a_2& 1& & & & \\ ⋮& & \ddots & & & \\ a_1& \cdots & \cdots & 1& & \\ ⋮& & & & \ddots & \\ a_n& & & & & 1\end{array}\right|=a_i$

所以所有满足于第二种情况的行列式之和为 $a_1+a_2+a_3+\cdots +a_n$ ，因此有

$F_n=1+a_1+a_2+\cdots +a_n$

8. 计算带状矩阵的行列式

还有一类特殊的行列式叫做带状行列式，下面计算一个特殊的带状矩阵的行列式 [6] 。

1) 试证： $\left|\begin{array}{cccccc}a+b& ab& 0& \cdots & 0& 0\\ 1& a+b& ab& \cdots & 0& 0\\ 0& 1& a+b& \cdots & 0& 0\\ ⋮& ⋮& ⋮& & ⋮& ⋮\\ 0& 0& 0& \cdots & 1& a+b\end{array}\right|=\frac{a^{n+1}-b^{n+1}}{a-b}$ $\left(a\ne b\right)$ 。

证：可以用数学归纳法证明。

当 $n=1$ 时，原式 $=a+b$ ；当 $n=2$ 时，原式 $=a^2+ab+b^2$ ，等式均成立。

假设当 $n=k$ 时等式成立；当 $n=k+1$ 时，

$\begin{array}{c}原式=\left(a+b\right)\cdot \left|\begin{array}{cccccc}a+b& ab& 0& \cdots & 0& 0\\ 1& a+b& ab& \cdots & 0& 0\\ 0& 1& a+b& \cdots & 0& 0\\ ⋮& ⋮& ⋮& & ⋮& ⋮\\ 0& 0& 0& \cdots & 1& a+b\end{array}\right|-\left|\begin{array}{cccccc}ab& 0& 0& \cdots & 0& 0\\ 1& a+b& ab& \cdots & 0& 0\\ 0& 1& a+b& \cdots & 0& 0\\ ⋮& ⋮& ⋮& & ⋮& ⋮\\ 0& 0& 0& \cdots & 1& a+b\end{array}\right|\\ =\left(a+b\right)\cdot \frac{a^{n+1}-b^{n+1}}{a-b}-ab\cdot \frac{a^n-b^n}{a-b}=\frac{a^{n+2}-b^{n+2}}{a-b}\end{array}$

所以当 $n=k+1$ 时，等式成立，证毕。

但对于一般形式的带状行列式，可能结果得到的式子就不会有这么好的对称性了，却很有研究价值。

2) 计算下列n阶带状矩阵的行列式：

$X_n=\left|\begin{array}{cccccc}a& b& 0& \cdots & 0& 0\\ c& a& b& \cdots & 0& 0\\ 0& c& a& \cdots & 0& 0\\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮\\ 0& 0& 0& \cdots & a& b\\ 0& 0& 0& \cdots & c& a\end{array}\right|$

不难得到关于 $X_n$ 的三项递推关系式：，其中 $X_1=a$ ， $X_2=a^2-bc$ 。 $X_n$ 实质上就是一个数列，对于这样的数列可以用特征方程去求解。

它的特征方程为 $y^2-ay+bc=0$ ，设此方程的两个根为 $y_1$ 和 $y_2$ ，有

$y_1=\frac{1}{2}a+\frac{1}{2}\sqrt{a^2-4bc}$ ， $y_2=\frac{1}{2}-\frac{1}{2}\sqrt{a^2-4bc}$

对于 $y_1$ 和 $y_2$ 的取值，需要做以下三类讨论：

① 当 $a^2-4bc>0$ 时， $y_1$ 和 $y_2$ 是两个不同的实根，则 $X_n=C_1{y}_1^n+C_2{y}_2^n$ ( $C_1$ 和 $C_2$ 为待定系数，它们的值取决于整个数列的前两项的值，即 $X_1$ 和 $X_2$ 的值，下同)。分别令 $n=1$ 和2，得到

$\{\begin{array}{l}{C}_1{y}_1+C_2{y}_2=X_1\\ C_1{y}_1^2+C_2{y}_2^2=X_2\end{array}$ ，解得 $C_1=\frac{X_2-X_1{y}_2}{y_1\left(y_1-y_2\right)}$ ， $C_2=\frac{X_2-X_1{y}_1}{y_2\left(y_2-y_1\right)}$ 。

② 当 $a^2-4bc<0$ 时， $y_1$ 和 $y_2$ 是两个相同的实根， $y_1=y_2=\frac{1}{2}a$ ，则 $X_n=\left(C_1+C_{2}n\right)y_1^n$ 。代入初值有

$\{\begin{array}{l}\left(C_1+C_2\right)y_1=X_1\\ \left(C_1+2C_2\right)y_1^2=X_2\end{array}$ ，解得 $C_1=\frac{2X_1{y}_1-X_2}{y_1^2}$ ， $C_2=\frac{X_2-X_1{y}_1}{y_1^2}$ 。

③ 当 $a^2-4bc<0$ 时，和是两个不同的复根 $r\left(\cos \theta \pm i\sin \theta \right)$ ，则

$X_n=r^n\left(C_1\cos n\theta +C_2\sin n\theta \right)$

这个问题我们不再继续对a，b，c的取值进行较为细致的分类讨论，此过程复杂而且繁琐，只要能够把一组具体的a，b，c的值所对应的行列式求解出来即可。

如果从归纳的角度来分析这个问题，得到的通项公式却是另一种结果。我们可以写出 $X_n$ 的前几项，再通过前几项归纳出 $X_n$ 的通项公式。

$\begin{array}{l}{X}_1=a\\ X_2=a^2-bc\\ X_3=a^3-2abc\\ X_4=a^4-3a^{2}bc+b^2{c}^2\\ X_5=a^5-4a^{3}bc+3a^2{b}^2{c}^2\end{array}$

$\begin{array}{l}{X}_6=a^6-5a^{4}bc+6a^2{b}^2{c}^2-b^3{c}^3\\ X_7=a^7-6a^{5}bc+10a^3{b}^2{c}^2-4a{b}^3{c}^3\\ X_8=a^8-7a^{6}bc+15a^4{b}^2{c}^2-10a^2{b}^3{c}^3+b^4{c}^4\\ X_9=\cdots \end{array}$

由此归纳 $X_n=a^n-C_{n-1}^1{a}^{n-2}bc+C_{n-2}^2{a}^{n-4}{b}^2{c}^2-C_{n-3}^3{a}^{n-6}{b}^3{c}^3+\cdots$ ，这个公式同样可以用数学归纳法进行证明，这里不再赘述。

通过以上两种方法均可以求出 $X_n$ 的表达式，但这两种表达式的形式却截然不同，那么这两种表达式之间是否存在一定的联系呢？

引申：如果把 $X_n$ 的每一项的系数的绝对值单独列出来，会组成一个这样的数表：

系数排布 每行求和

1 1

1 1 2

1 2 3

1 3 1 5

1 4 3 8

15 6 1 13

1 6 104 21

1 7 15101 34

1 8 21205 55

1 9 2835151 89

整个系数的排布就像是一个斜着的杨辉三角形，只不过杨辉三角形的每一横行在这里变成了一条由左上至右下的一条斜线了。而有意思的是每一行求和后组成的数列刚好都符合斐波那契数列的每一项。

此时不妨令 $a=1$ ， $b=1$ ， $c=-1$ ，这样 $X_n$ 当中的每一项 $X_i$ 的值刚好就等于对应的那一行(即第i行)的系数的绝对值之和，即 $X_1=1$ ， $X_2=2$ ， $X_3=3$ ， $X_4=5$ ， $\cdots$ 同样的还可以得到 $X_n=C_n^0+C_{n-1}^1+C_{n-2}^2+\cdots$ ，这都与斐波那契数列当中的某些项是对应的。

而从递推关系的角度来看，关于数列 $X_n$ 的递推公式为 $X_n=X_{n-1}+X_{n-2}$ ，也刚好符合斐波那契数列 $X_n$ 的递推公式，只不过数列的前两项与斐波那契数列不同，刚好错了一位。

不妨设斐波那契数列的通项公式为 $A_n$ ，那么不难得到

$A_n=X_{n-1}=C_{n-1}^0+C_{n-2}^1+C_{n-3}^2+\cdots \left(n\ge 2\right)$

当 $n=1$ 时， $A_n=C_0^0=1$ ，刚好也满足于上述的通项公式。这便是斐波那契数列的通项公式的另一种表现形式： $A_n=C_{n-1}^0+C_{n-2}^1+C_{n-3}^2+\cdots$ ，有别于用特征方程所得到的通项公式

$A_n=\frac{\sqrt{5}}{5}\left[{\left(\frac{1+\sqrt{5}}{2}\right)}^n-{\left(\frac{1-\sqrt{5}}{2}\right)}^n\right]$

但二者实际上是等价的。

这里不仅在于解决了一种特殊类型的行列式，更重要的是还通过对数列的归纳找到了杨辉三角，与斐波那契数列之间的潜在联系，并通过这种联系找到了斐波那契数列通项公式的另一种表示方法。

9. 计算范德蒙德矩阵的行列式

范德蒙德矩阵的行列式是计算其他矩阵行列式的基础，这里简单讨论。计算下列n阶范德蒙德矩阵的行列式：

$x_n=\left|\begin{array}{ccccc}1& 1& 1& \cdots & 1\\ a_1& a_2& a_3& \cdots & a_n\\ a_1^2& a_2^2& a_3^2& \cdots & a_n^2\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ a_1^{n-1}& a_2^{n-1}& a_3^{n-1}& \cdots & a_n^{n-1}\end{array}\right|$

从第n行开始，每一行减去前一行的 $a_1$ 倍，即 $r_n-a_1{r}_{n-1}$ ， $r_{n-1}-a_1{r}_{n-2}$ ， $\cdots$ ， $r_2-a_1{r}_1$ ，目的是将行列式的第一列的除了首个元素的其他元素的值全变为0。即

$x_n=\left|\begin{array}{cccccc}1& 1& 1& \cdots & 1& 1\\ 0& a_2-a_1& a_3-a_1& \cdots & a_{n-1}-a_1& a_n-a_1\\ 0& a_2^2-a_2{a}_1& a_3^2-a_3{a}_1& \cdots & a_{n-1}^2-a_{n-1}{a}_1& a_n^2-a_n{a}_1\\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮\\ 0& a_2^{n-2}-a_2^{n-3}{a}_1& a_3^{n-2}-a_3^{n-3}{a}_1& \cdots & a_{n-1}^{n-2}-a_{n-1}^{n-3}{a}_1& a_n^{n-2}-a_n^{n-3}{a}_1\\ 0& a_2^{n-1}-a_2^{n-2}{a}_1& a_3^{n-1}-a_3^{n-2}{a}_1& \cdots & a_{n-1}^{n-1}-a_{n-1}^{n-2}{a}_1& a_n^{n-1}-a_n^{n-2}{a}_1\end{array}\right|$

然后把每一列的公因式提出来

$\begin{array}{c}{x}_n=\left|\begin{array}{ccccc}{a}_2-a_1& a_3-a_1& \cdots & a_{n-1}-a_1& a_n-a_1\\ a_2\left(a_2-a_1\right)& a_3\left(a_3-a_1\right)& \cdots & a_{n-1}\left(a_{n-1}-a_1\right)& a_n\left(a_n-a_1\right)\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ a_2^{n-3}\left(a_2-a_1\right)& a_3^{n-3}\left(a_3-a_1\right)& \cdots & a_{n-1}^{n-3}\left(a_{n-1}-a_1\right)& a_n^{n-3}\left(a_n-a_1\right)\\ a_2^{n-2}\left(a_2-a_1\right)& a_3^{n-2}\left(a_3-a_1\right)& \cdots & a_{n-1}^{n-2}\left(a_{n-1}-a_1\right)& a_n^{n-2}\left(a_n-a_1\right)\end{array}\right|\\ =\left(a_2-a_1\right)\left(a_3-a_1\right)\cdots \left(a_n-a_1\right)\left|\begin{array}{ccccc}1& 1& \cdots & 1& 1\\ a_2& a_3& \cdots & a_{n-1}& a_n\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ a_2^{n-3}& a_3^{n-3}& \cdots & a_{n-1}^{n-3}& a_n^{n-3}\\ a_2^{n-2}& a_3^{n-2}& \cdots & a_{n-1}^{n-2}& a_n^{n-2}\end{array}\right|\end{array}$

上式当中的行列式就是 $n-1$ 阶范德蒙德行列式，这就是它的递推关系式。继续展开，得到

$x_n=\left(a_2-a_1\right)\left(a_3-a_1\right)\cdots \left(a_n-a_1\right)\cdot \left(a_3-a_2\right)\left(a_4-a_2\right)\cdots \left(a_n-a_2\right)\left|\begin{array}{ccccc}1& 1& \cdots & 1& 1\\ a_3& a_4& \cdots & a_{n-1}& a_n\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ a_3^{n-4}& a_4^{n-4}& \cdots & a_{n-1}^{n-4}& a_n^{n-4}\\ a_3^{n-3}& a_4^{n-3}& \cdots & a_{n-1}^{n-3}& a_n^{n-3}\end{array}\right|$

继续进行展开，一直展开到最后只剩下一个二阶行列式，即 $\left|\begin{array}{cc}1& 1\\ a_2& a_1\end{array}\right|=a_2-a_1$ ，也就是范德蒙德行列式可以分解成若干项的乘积的形式，只需从原始的行列式中的第二行任意选出两个数作差(这两个数当中靠右的那个数减去靠左的的那个数)，再把所有的项进行连乘，就能得到最后的结果，即

$x_n={\displaystyle \underset{1\le i<j\le n}{\prod }\left(a_j-a_i\right)}$

10. 范德蒙德矩阵的行列式的扩展

对于一个残缺的范德蒙德行列式，比如范德蒙德行列式当中少了某一行或者两行，再增加几列，或者这个行列式当中只有奇数次方项，那么这个行列式是否还能求解呢？答案是肯定的，下面举一些例子。

例：计算行列式 $\left|\begin{array}{cccc}1& 1& 1& 1\\ a_1& a_2& a_3& a_4\\ a_1^2& a_2^2& a_3^2& a_4^2\\ a_1^4& a_2^4& a_3^4& a_4^4\end{array}\right|$ 的值。

令此行列式的值为m。首先按照范德蒙德行列式的形式把这个行列式补齐，即

$\left|\begin{array}{ccccc}1& 1& 1& 1& 1\\ a_1& a_2& a_3& a_4& x\\ a_1^2& a_2^2& a_3^2& a_4^2& x^2\\ a_1^3& a_2^3& a_3^3& a_4^3& x^3\\ a_1^4& a_2^4& a_3^4& a_4^4& x^4\end{array}\right|$

此行列式展开后必然会得到一个关于x的五次多项式，其中 $a_1$ 、 $a_2$ 、 $a_3$ 、 $a_4$ 为这个五次多项式的多项式系数。

行列式m就是上述行列式中x³这一项的余子式，由于x³这一项在第四行第五列，所以x³的代数余子式的值是−m。从另一个角度去考虑，x³的代数余子式的值−m就是上述行列式展开之后x³项的系数，这样二者之间就联系起来了。

$\left|\begin{array}{ccccc}1& 1& 1& 1& 1\\ a_1& a_2& a_3& a_4& x\\ a_1^2& a_2^2& a_3^2& a_4^2& x^2\\ a_1^3& a_2^3& a_3^3& a_4^3& x^3\\ a_1^4& a_2^4& a_3^4& a_4^4& x^4\end{array}\right|=\left(x-a_1\right)\left(x-a_2\right)\left(x-a_3\right)\left(x-a_4\right){\displaystyle \underset{1\le i<j\le 4}{\prod }\left(a_j-a_i\right)}$

其中x³的系数为 $-\left(a_1+a_2+a_3+a_4\right){\displaystyle \underset{1\le i<j\le 4}{\prod }\left(a_j-a_i\right)}$ ，所以原行列式的值为。

$m=\left(a_1+a_2+a_3+a_4\right){\displaystyle \underset{1\le i<j\le 4}{\prod }\left(a_j-a_i\right)}$

对于只有奇数次方的范德蒙德行列式的求解过程比较复杂，这里不进行一般化的讨论，只拿出一个特殊的例子进行分析。

例：计算奇数次范德蒙的行列式 $\left|\begin{array}{cccc}1& 1& 1& 1\\ a_1& a_2& a_3& a_4\\ a_1^3& a_2^3& a_3^3& a_4^3\\ a_1^5& a_2^5& a_3^5& a_4^5\end{array}\right|$ 的值。

设此行列式的值为m。解决这个问题需要在这个行列之中添加两行两列，即

$\left|\begin{array}{cccccc}1& 1& 1& 1& 1& 1\\ a_1& a_2& a_3& a_4& x& y\\ a_1^2& a_2^2& a_3^2& a_4^2& x^2& y^2\\ a_1^3& a_2^3& a_3^3& a_4^3& x^3& y^3\\ a_1^4& a_2^4& a_3^4& a_4^4& x^4& y^4\\ a_1^5& a_2^5& a_3^5& a_4^5& x^5& y^5\end{array}\right|$

先以 $x^2$ 项进行展开，然后再以 $y^4$ 项进行展开，就可出现题目中的行列式的形式，只不过它的值为−m。而−m刚好就是上述行列式展开后的结果当中 $x^2{y}^4$ 项的系数，二者是一一对应的，所以上述行列式的值为

$\left(x-a_1\right)\left(x-a_2\right)\left(x-a_3\right)\left(x-a_4\right)\left(y-a_1\right)\left(y-a_2\right)\left(y-a_3\right)\left(y-a_4\right)\underset{\_}{\left(y-x\right)}{\displaystyle \underset{1\le i<j\le 4}{\prod }\left(a_j-a_i\right)}$

当划线部分取y时， $x^2{y}^4$ 项的系数为

$-\left({\displaystyle \underset{1\le i<j\le 4}{\prod }{a}_i{a}_j}\right)\left(a_1+a_2+a_3+a_4\right){\displaystyle \underset{1\le i<j\le 4}{\prod }\left(a_j-a_i\right)}$

当划线部分取−x时， $x^2{y}^4$ 项的系数为

$\left(a_1{a}_2{a}_3+a_1{a}_2{a}_4+a_1{a}_3{a}_4+a_2{a}_3{a}_4\right){\displaystyle \underset{1\le i<j\le 4}{\prod }\left(a_j-a_i\right)}$

所以 $x^2{y}^4$ 项的系数为

${\displaystyle \underset{1\le i<j\le 4}{\prod }\left(a_j-a_i\right)}\left[\left({\displaystyle \underset{1\le i<j<k\le 4}{\prod }{a}_i{a}_j{a}_k}\right)-\left({\displaystyle \underset{1\le i<j\le 4}{\prod }{a}_i{a}_j}\right)\left(a_1+a_2+a_3+a_4\right)\right]$

因此给定的行列式的值为

${\displaystyle \underset{1\le i<j\le 4}{\prod }\left(a_j-a_i\right)}\left[\left({\displaystyle \underset{1\le i<j\le 4}{\prod }{a}_i{a}_j}\right)\left(a_1+a_2+a_3+a_4\right)-\left({\displaystyle \underset{1\le i<j<k\le 4}{\prod }{a}_i{a}_j{a}_k}\right)\right]$

11. 结语

本文讨论一些特殊矩阵的行列式计算问题，包括友矩阵的特征多项式的计算。针对一些特殊矩阵，如带状矩阵、块单位阵的行列式或特征多项式的求解方法，有的运用归纳法，对于一个n阶行列式，处理起来可能比较困难，这时可以将问题简单化，进行局部的试验研究，当n的值比较小时可以算出行列式的值，比如令 $n=1$ ， $n=2$ 等进行计算，从这些计算结果当中进行归纳得到一般项的结果，再从归纳的角度进行证明，比如运用数学归纳法进行证明得到结果。