基于改进的蚁群算法的围堵罪犯模型

An Improved Ant Colony Algorithm-Based Model for Blocking Criminals

摘要: 交巡警服务平台散布在城区，能够依托情报系统实行联动，不但对犯罪分子起到震慑作用，而且对于突发重大刑事案件能进行快速反应。针对交巡警围堵罪犯问题，提出了一种每支警队可连续封锁多个路口的新型围堵方案。建立了封锁路线选择模型、封锁任务完成判定模型和路口封锁状态更新模型。使用了改进的蚁群算法，该算法在通常的蚁群算法中增加了任务否决变异机制。最后根据某市区的实际道路情况进行模拟，并分析证明了结果的合理性与算法的有效性。

Abstract: Traffic and patrol police service platforms are scattered in urban areas, which can rely on intelli-gence system to implement linkage. They not only deter criminals, but also respond quickly to sudden major criminal cases. Aiming at the problem of traffic and patrol police blocking criminals, this paper proposes a new blocking scheme, in which each police unit can block multiple intersec-tions continuously. A blockade route selection model, a blockade task completion decision model and an intersection blockade status update model are established. An improved ant colony algo-rithm is used, which adds a task rejection mutation mechanism to the common ant colony algorithm. Finally, according to the actual road situation of a certain urban area, the simulation and analysis prove the rationality of the results and the effectiveness of the algorithm.

1. 引言

在发生突发事件后，制定快速有效的围堵犯罪嫌疑人的方案是十分重要的。然而，日益复杂的交通网络给围堵工作带来了很大的困难。针对此问题，董小小等人提出了最小封堵圈的扩张算法 [1] ；周伟刚等人提出了点截集的围堵模型 [2] ；杨敏等人提出了基于闭集的快速围堵算法 [3] ；董金哲等人利用图论建立了围捕模型 [4] 。

上述研究都在一定程度上解决了围堵罪犯问题，但目前的路线封锁思想主要为简单的“一次性封锁”，即每个警队至多只能封锁一个路口，一旦一个警队对某个路口完成封锁后就不再执行其余任务，如此封锁可能会造成封锁范围过大而增加后续搜捕难度，所以通过现有的封锁方法往往不能达到及时封锁的目的。

本文在建立模型时，设计每支警队可以连续封锁多个路口的封锁方案来对罪犯进行围堵，通过对是否封锁路口的判断，对封锁路口先后顺序的选择，以达到提高封锁效率、减少对警力资源的要求的目的。

2. 模型的建立

2.1. 封锁路线选择体系的建立

罪犯从 $P$ 点开始逃跑，由于不知其具体逃跑方向，所以其之后可能的逃跑范围应为以 $P$ 点为中心、以 $R\left(t\right)$ 为辐散长度沿与 $P$ 连接的路线向外围辐散的区域，设罪犯的逃跑速度为 $V_1$ ，则 $R\left(t\right)$ 的计算公式如下：

$R\left(t\right)=v_1\cdot t$ (1)

设序号为 $i$ 的路口距离 $P$ 点的距离为 $x_i$ ，当 $P$ 点确定下来后， $x_i$ 就随之确定下来了。设罪犯从 $P$ 点开始逃跑到警察接到报警之间的时间为 $t_c$ 。设 $t$ 时刻第 $j$ 号警队距离第 $i$ 号路口的距离为 $r_{ij}\left(t\right)$ 。要对罪犯进行封锁，即要对 $t$ 时刻罪犯还未到达的路口进行封锁才可对罪犯完成封锁，其计算公式如下：

$R\left(t\right)\le x_i,\left(t\ge t_c,i\in A\right)$ (2)

其中 $A$ 为所有路口序号的集合。在 $t$ 时刻满足上式的路口才可被封锁。

对某个路口进行封锁还需警队在规定时间内能够赶到待封锁的路口，因此有如下约束条件：

$\frac{r_{ij}\left(t_{j1}\right)}{v_2}+t_{j1}\le t$ (3)

其中 $t_{j1}$ 为第 $j$ 号警队在刚到当前所在路口的时刻。

当满足(3)式时，第 $j$ 号警队才可前往第 $i$ 号路口进行封锁，且更新 $t_{j1}$ 的值以及相应的 $r_{ij}\left(t_{j1}\right)$ ， $t_{j1}$ 的计算公式如下：

$t_{j1}=\frac{r_{ij}\left(t_{j1}\right)}{v_2}+t_{j1}$ (4)

在警队对路口封锁时，假设警队到达路口后进行封锁的时间可忽略不计。

2.2. 封锁任务完成的确定

对罪犯而言，若警察未对其完成封锁，则意味着罪犯还可以从其当前已到达区域内某一路口向另一个未被封锁且罪犯尚未经过的路口逃跑。此处设 $D_{\text{1}}$ 为 $t$ 时刻罪犯已经经过的路口序号的集合， $D_2$ 为 $t$ 时刻未被封锁的路口的集合， $D_3$ 为 $t$ 时刻可以供罪犯选为下一个逃跑的路口序号的集合，则有如下关系式：

$\begin{array}{l}{D}_1\subseteq A\\ D_2\subseteq A\\ D_3\subseteq D_2\\ D_1\cap D_3=\varphi \end{array}$ (5)

根据 $D_3$ 的定义可知，当 $D_3=\varphi$ 时即完成了全部封锁任务，其对应的时刻即为完成所有任务的时刻，记为 $t_{all}$ 。

2.3. 路口状态的确定

当罪犯的逃跑区域扩大覆盖到序号为 $i$ 的路口时，该路口的状态可有两种：

1) 该路口已被封锁。

2) 该路口尚未被封锁。

设第 $i$ 号路口状态为 ${\text{flag}}_i$ ，第 $i$ 号路口尚未被封锁且罪犯尚未经过该路口时 ${\text{flag}}_i=0$ ；第 $i$ 号路口已被封锁时 ${\text{flag}}_i=1$ ；第 $i$ 号路口尚未被封锁且罪犯已经过该路口时 ${\text{flag}}_i=2$ 。所以当 ${\text{flag}}_i=2$ 时， $i\in D_1$ ，即：

$D_1=\left\{i\in A|{\text{flag}}_i=2\right\}$ (6)

对于 $D_1$ 中的元素，其在未被纳入 $D_1$ 中时，需有如下条件：

${\text{flag}}_i=0,\left(R\left(t\right)=x_i\right)$ (7)

即在罪犯当前可到达区域的边界刚刚覆盖到该路口时，该路口须还是未被封锁的路口。对于罪犯下一个逃往的路口，其必须是罪犯已经经过的某个路口的邻接路口，即对于下一个逃往的路口 $i\in D_2$ ，存在 $i_1\in D_1$ 使得 $i$ 与 $i_1$ 邻接：

$M\left(i,i_1\right)=1,i\in D_2,i_1\in D_1$ (8)

其中 $M$ 为罪犯的路口邻接矩阵，元素取1表示对应路口邻接，取0表示对应路口不邻接。

同时满足公式(7)、(8)时，其所对应的 $i$ 才可选入 $D_1$ 中，即：

$\{\begin{array}{l}{\text{flag}}_i=2,\text{if}\{\begin{array}{l}{\text{flag}}_i=0\\ R\left(t\right)=x_i\\ {\displaystyle \underset{i_1}{\sum }M\left(i,i_1\right)}\ge 1,i_1\in D_1\\ i\in D_2\end{array}\\ {\text{flag}}_i={\text{flag}}_i,\text{else}\end{array}$ (9)

根据 $D_2$ ， $D_{\text{3}}$ 的定义可知有如下公式：

$D_3=\left\{i\in D_2|{\displaystyle \underset{i_1}{\sum }M\left(i,i_1\right)}\ge 1,i_1\in D_1\right\}$ (10)

于是(9)式化简为：

$\{\begin{array}{cc}{\text{flag}}_i=2& \text{if}\{\begin{array}{l}{\text{flag}}_i=0\\ R\left(t\right)=x_i\\ i\in D_3\end{array}\\ {\text{flag}}_i={\text{flag}}_i& \text{else}\end{array}$ (11)

由(5)式还可知：

$D_3=D_3-\left\{i\right\},\text{if}{\text{flag}}_i=2$ (12)

2.4. 目标函数求解

本文设计新的封锁方案时，主要考虑实现如下几个目标：

1) 完成所有封锁任务的总用时尽量短；

2) 封锁的区域面积尽量少；

3) 被封锁的路口数量尽量少。

虽然在设计方案时希望找到符合上述目标的最优方案，但最终求得的结果很难同时满足上述三个目标分别达到最优解，因此需划分上述三个目标的优先级。封锁问题首要目的是在最短时间内完成围堵，因此考虑将目标1作为一级目标。因为若封锁区域过大，罪犯对封锁区域内的人群会造成更大的威胁，且逮捕难度也会大大增加，所以要在保证完成封锁任务的条件下，使封锁区域的面积尽量小，因此考虑以目标2作为二级目标。当被封锁路口数过多时，需要耗费更多的警力资源，且封锁时间和封锁区域的面积也可能会相应增多，所以考虑以目标3作为三级目标。

对一级目标和三级目标的求解分别如(13)、(14)式所示：

$\min t_{all}$ (13)

$\min \Vert \left\{i\in A|{\text{flag}}_i=1\right\}\Vert$ (14)

在计算二级目标时，我们考虑封锁面积一般为不规则图形，所以计算起来较为繁琐，因此本文中考虑以罪犯已经经过的路口数替代封锁面积来进行计算，于是二级目标计算公式为：

$\min \Vert D_1\Vert$ (15)

3. 模型的求解与算法设计

3.1. 改进的蚁群算法

在 $n$ 个路口中去依此搜索对应路口进行的封锁，继而对罪犯完成封锁任务，这是一个 $NP$ 问题。因此在实际求解时，通常需要利用启发式算法对问题进行求解。若用简单的蚁群算法 [5] [6] [7] ，则在搜索中很容易陷入对局部最优解的搜索，因此，本文采用改进的蚁群算法来对问题进行求解。我们在通常的蚁群算法中增加了任务否决变异机制，其主要思路为：当选定了某个位置的警队去执行当前路口的封锁任务时，以一定概率取消此次任务，这样就能够一定程度上避免局部搜索最优解的情况。为方便起见，之后我们称当前时刻需判断是否应被封锁的路口为目标路口。改进的蚁群算法步骤如下：

1) 初始化信息素矩阵

信息素矩阵是一个 $n$ 维矩阵，记作 $BR$ ， $n$ 表示路口总个数， $BR\left(i,j\right)$ 表示第 $$ 个路口的警察去第 $j$ 个路口进行封锁的匹配选择概率， $BR$ 的每一个元素初始化为0.5。

2) 封锁匹配选择算子：

搜索现在可以去封锁目标路口的警队，若搜索结果为空，则目标路口不能被封锁，若不为空则利用轮盘赌算法 [8] [9] ，求出各候选警队去执行此次封锁任务的概率 $p$ ，并依概率随机选出执行此次任务的警队序号。 $p$ 的计算方法如下：

$p\left(i,j\right)=\{\begin{array}{cc}\frac{BR{\left(i,j\right)}^{\alpha }\cdot {\left(1/S\left(i,j\right)\right)}^{\beta }}{{\displaystyle \underset{i}{\sum }BR{\left(i,j\right)}^{\alpha }\cdot {\left(1/S\left(i,j\right)\right)}^{\beta }}}& j\in POL\\ 0& \text{else}\end{array}$ (16)

其中 $POL$ 为候选警队序号集合， $\alpha$ 为信息素重要程度的参数， $\beta$ 为启发式因子重要程度参数， $S\left(i,j\right)$ 为当前罪犯从第 $i$ 个路口到第 $j$ 个路口之间的最短距离。

3) 任务否决变异机制：

固定执行任务否决变异概率，产生一个0至1之间的随机数，若随机数小于变异概率，则警队不执行此次封锁任务，反之则执行。

4) 更新路口状态：

每个路口的封锁状态存放到矩阵 $\text{Flag}$ 中，若路口被封锁则取1，否则取0，更新目标路口在 $\text{Flag}$ 中的数值。若目标路口被封锁，则删除与目标路口关联的有向路线更新 $S$ 矩阵。

5) 更新信息素矩阵：

信息素矩阵 $BR$ 中元素以挥发率 $\mu$ 进行挥发：

$B{R}_{ij}\left(t+1\right)=B{R}_{ij}\left(t\right)\cdot \left(1-\mu \right),\left(i,j\in A\right)$ (17)

根据此次循环的二级目标值和三级目标值更新信息素矩阵 $BR$ ：

$B{R}_{ij}\left(t+1\right)=B{R}_{ij}\left(t+1\right)+\left(1-B{R}_{ij}\left(t+1\right)\right)\cdot \left({\displaystyle \underset{i}{\overset{3}{\sum }}{\text{goal}}_i\cdot {\lambda }_i}\right)$ (18)

${\text{goal}}_i=\frac{g_i-\min G_i}{\max \left\{g_i+G_i\right\}-\min \left\{g_i+G_i\right\}}$ (19)

其中 $g_i$ 表示此次循环的第 $i$ 级目标值， $G_i$ 表示此前循环求得的 $g_i$ 元素组成的集合， $i=\text{1},\text{2},\text{3}$ ， ${\lambda }_i$ 为第 $i$ 级目标值的权重。

算法具体流程图如图1所示。

3.2. 警队最优封锁方案求解

Step 1：利用 $\text{Floyd}$ 算法求各路口之间的最短路程。

Step 2：随机生成 $P$ 点作为罪犯初始逃跑地点， $N=0$ 。

Step 3：初始化参数，令 $k=1$ 。

Step 4：计算 $P$ 点与各路口的最短路程及对应路线，存储到集合 $H$ 中。

Step 5：计算在 $H$ 条件下 $P$ 点与各个路口的距离所对应的时间，降序存储到 $T\left(k\right)$ 向量中。

Step 6：对 $T\left(k\right)$ 时刻对应的路口进行封锁任务选择。

Step 7：更新所有路口当前封锁状态，更新集合 $H$ ，令 $k=k+1$ 。

Step 8：判断对罪犯的全部封锁任务是否全部完成，若未完成则返回Step 4。

Step 9：计算三个目标函数值，并令 $N=N+1$ ，若 $N<N_{\max }$ 则返回Step 3。

Step 10：求 $\min t_{all}$ 、 $\min \Vert D_1\Vert$ 、 $\min \Vert \left\{i\in A|fla{g}_i=1\right\}\Vert$

警队最优封锁方案求解完整的算法流程图如图2所示。

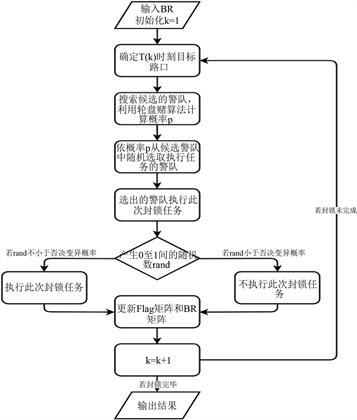
Figure 1. Flow chart of improved ant colony algorithm

图1. 改进得蚁群算法流程图

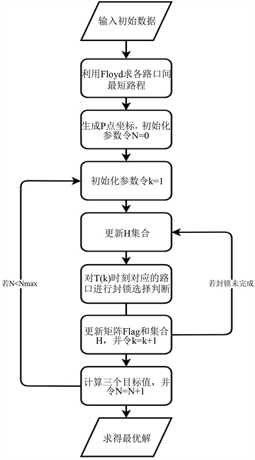
Figure 2. Flow chart for solving optimal blockade scheme

图2. 最优封锁方案求解流程图

4. 实例分析

现以2011年全国大学数学建模竞赛B题道路数据为例，利用上述算法进行模拟仿真。考虑罪犯在逃跑时将以尽可能快的速度逃离现场，并参考当地道路限速，因此假设罪犯的逃跑速度为60 km/h。假设接警后警车的行驶速度为60 km/h，且假设警队到达路口后封锁当下所在路口的时间忽略不计。

取接警时间间隔为3 min，任务否决变异概率为0.1， ${\lambda }_{\text{1}}$ 为0.5， ${\lambda }_2$ 为0.33， ${\lambda }_3$ 为0.17，初始逃跑地点为32号路口，初始路口封锁选择矩阵各元素值为0.5， $\alpha$ 值取1， $\beta$ 值取7， $\mu$ 取0.3，迭代次数为100，进行计算机仿真模拟，表1列出求解得到的部分结果：

Table 1. Solution results of three objective values

表1. 三种目标值求解结果

求解得到的最优封锁方案对应的警队封锁路线如表2所示：

Table 2. Optimal blockade scheme

表2. 最优封锁方案

最优解封锁示意图如图3所示：

其中正方形处为被封锁的路口，五角星处为罪犯最初逃跑位置，菱形处为各个路口位置。

最优方案对应的三个目标值分别为：

1) 总封锁用时：0.3050小时

2) 封锁区域内包含的路口数：27个

3) 被封锁的路口数：21个

下面是迭代的100次每次求解的总封锁时间：

图4的横坐标为迭代次数，纵坐标为总封锁时间。由图4可知算法收敛性较好。

5. 结论

本文研究了围堵罪犯问题，建立了封锁路线选择模型、封锁任务完成判定模型和路口封锁状态判定模型。设计并实现了改进的蚁群算法，求解出封锁罪犯的最佳围堵方案和最短封锁时间，提高了封锁效率。模型的求解算法全面严谨，有较大的实际应用价值。

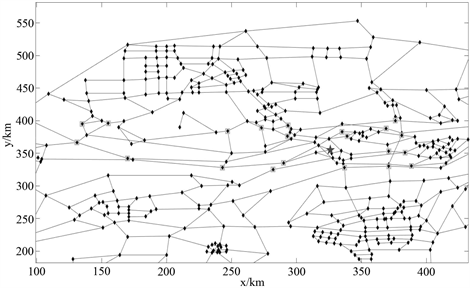
Figure 3. Schematic diagram of optimal blockade scheme

图3. 最优封锁方案示意图

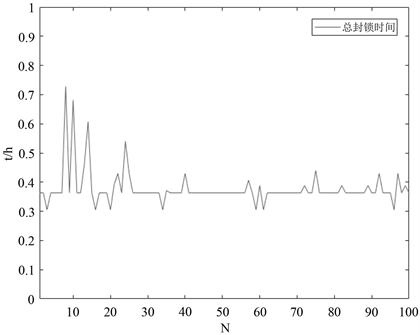
Figure 4. Effect of iteration number on total blockade time

图4. 迭代次数对总封锁时间的影响

本文中构建的模型未考虑若警队在执行当前任务时经过了未来需要被封锁的路口时是否对其进行封锁的问题，若警队在前往目标路口的过程中经过并封锁未来需要封锁的路口，可能会进一步提高封锁效率。本文中的算法因为利用了蚁群算法的思想，在执行程序时运行时间过长，从而要求算法迭代次数不宜过大，因此进一步优化程序算法和有关参数可能会得到更理想的结果。