矿山围岩蠕变破坏过程数值模拟

Numerical Simulation of Creep Failure Process of Mine Surrounding Rock

摘要: 矿山开采中围岩的蠕变特性是影响岩体工程长期稳定的重要因素。本文在幂函数模型基础上，基于损伤力学理论，建立了能够描述加速蠕变过程的非线性蠕变损伤模型。模型采用最大拉应变准则和摩尔–库仑准则作为损伤判断准则。借助有限元分析软件编程实现该模型的数值求解。首先将数值模拟得到的结果与已有试验数据进行对比分析，验证了模型的正确性。然后进行了单轴和三轴压缩蠕变数值模拟，模拟得到了岩石蠕变破裂的3个典型阶段，即初始、稳定和加速蠕变阶段。研究结果表明：所建立的蠕变模型适合于模拟预测岩石的蠕变破坏，复杂的宏观蠕变破坏可以用细观单元的损伤来解释。

Abstract: Creep property of rock mass has a significant impact on the stability of underground constructions. On the basis of classical power-law creep model, the time-dependent creep behavior of rock is in-vestigated based on damage mechanics principle, in which the damage evolution is considered as a key factor dominating the accelerating creep and a damage-based constitutive law for tertiary creep is proposed. The maximum tensile strain criterion and the Mohr-Coulomb criterion are utilized as two damage thresholds to control the rock damage. Then the damage-based creep model is implemented using finite element method by MATLAB programming, a powerful PDE-based multiphysics modeling environment. The model is firstly validated by comparing the numerical results with the previously published experimental observation and then used to simulate the rock creep under uniaxial and biaxial compression. The model accurately reproduces the classic tri-modal behaviour (primary, secondary and tertiary creep) seen in laboratory creep (constant stress) experiments. So the fact shows that the rheological model is appropriate to predict the nonlinear creep failure of rocks, and the complex macroscopic time-dependent behavior can be mechanically explained by the material degradation (damage) at the mesoscale.

1. 引言

矿山围岩的蠕变性是岩石的重要力学特性，许多岩体工程的失稳破坏都与蠕变变形有密切关系 [1] [2] [3] 。蠕变特性是用以解释和分析岩体工程长期稳定的重要依据。因此，深入研究岩石的蠕变特性具有重要的理论价值和实践意义。

对蠕变特性的研究多采用试验研究和理论分析的方法。岩石蠕变试验是认识岩石蠕变性质的主要途径和重要手段，通过对试验数据进行拟合分析和在一定假设基础上展开理论推演，得到相应的岩石蠕变本构模型 [4] [5] [6] 。在理论研究方面，通常采用如下三种方法建立蠕变模型：一种是通过流变试验，采用经验方程拟合岩石流变试验曲线 [7] ；二是基于流变试验结果，采用模型元件建立岩石流变模型，通过参数辨识、反演等方法确定出模型参数 [8] ；三是采用损伤力学理论来建立岩石流变模型 [9] 。应用损伤理论建立的蠕变损伤模型，可以较为满意地描述岩石的蠕变损伤特性，并考虑岩石的延展性变形、变位、变形硬化和变形恢复、损伤及损伤复原机制等。损伤理论应用于岩石流变分析中，首先损伤会引起岩石的非弹性流动，进而过渡到蠕变阶段，并在加速蠕变阶段损伤累积，直至最终发生加速蠕变破坏。缪协兴和陈至达 [10] 基于岩石蠕变试验结果，总结出了以能描述损伤历史的蠕变模量为参数的岩石蠕变损伤方程，由该方程能方便地定出任意蠕变时刻的损伤状态和进行蠕变损伤的测定。杨春和等 [11] 在谢和平 [12] 提出的岩石蠕变损伤模型的基础上建立了一种能反映盐岩蠕变全过程的蠕变损伤模型，且模型参数较少，便于从实验中求取。张强勇等 [13] 在考虑岩体的流变损伤劣化效应的基础上，建立了一个变参数的蠕变损伤模型，并推导了模型的三维差分表达式，将其在FLAC3D软件中实现了模块程序化，在大岗山水电站坝基边坡工程得到了应用。佘成学 [14] 引进岩石时效强度理论和Kachanov损伤理论，建立了以时间变量表示的岩石损伤表达式，并与黏塑性流变参数相联系，建立了黏塑性流变参数非线性表达式。

找到一种合理的方法将微观裂纹的扩展和宏观形式的破坏连接起来是蠕变模型研究的重点。典型的岩石蠕变全过程曲线包括三个阶段，减速和稳定阶段占据了大部分时间，加速蠕变阶段只有很小的一部分。虽然加速蠕变阶段所占时间很短，但加速蠕变在岩石的失稳破坏过程中却起着极其重要的作用，岩石的失稳破坏就是在这一阶段产生的。因此，本文在细观损伤力学的基础上建立了能够描述岩石加速蠕变的非线性蠕变损伤力学模型。通过与已有试验数据进行对比验证所建立模型的正确性，运用所建立的模型进行了蠕变数值模拟。

2. 蠕变损伤模型建立

2.1. 蠕变本构模型

蠕变试验过程中，在加载初始阶段存在瞬时的弹性变形，随加载时间增长，岩石的蠕变变形增加，此部分应变为蠕变应变。因此，假定岩石的应变由弹性应变和蠕变应变两部分组成：

$\epsilon ={\epsilon }_{\text{e}}+{\epsilon }_{\text{c}}$ (1)

岩石的蠕变本构关系采用如下的表达式示：

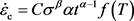(2)

式中： ${\stackrel{\dot{}}{\epsilon }}_{\text{c}}$ 为蠕变应变率； $\sigma$ 为轴向应力；C、 $\beta$ 和 $\alpha$ 为与材料有关的常数；，其中

B是比例因子， $\Delta H$ 是活化能，R是普适气体常数，T是温度。

由公式可知，在温度相等的条件下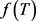，是常数，因此公式(2)经过简化可以用下式表达：

${\stackrel{\dot{}}{\epsilon }}_{\text{c}}=A{\sigma }^{\beta }\alpha t^{\alpha -1}$ (3)

式中：A为常数。

公式(3)表达的是一维状态下的本构方程，在实际问题中通常要采用三维模型，因此推广到三维条件下的表达式为

(4)

式中： ${\stackrel{\dot{}}{\epsilon }}_{cij}$ 为蠕变应变率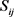；为偏应力。 ${\sigma }_{\text{e}}$ 是有效应力，可定义为：

${\sigma }_{\text{e}}=\left(\frac{1}{\sqrt{2}}\right){\left[{\left({\sigma }_{11}-{\sigma }_{22}\right)}^2+{\left({\sigma }_{33}-{\sigma }_{22}\right)}^2+{\left({\sigma }_{11}-{\sigma }_{33}\right)}^2+6\left({\sigma }_{12}^2+{\sigma }_{23}^2+{\sigma }_{13}^2\right)\right]}^{\frac{1}{2}}$ (5)

对公式(4)进行分析，可以知道它只能描述蠕变的前两个阶段，对于加速蠕变阶段无法进行模拟 [15] 。而岩石的加速蠕变阶段是本文研究的重点，需要建立一个非线性加速蠕变模型。

2.2. 损伤演化方程

岩石在受到压力后会在内部产生损伤区，损伤的累积会导致岩石的最总破裂，本文采用唐春安教授团队 [16] 提出的具有残余强度的弹性损伤关系(如图1所示)，结合前面的蠕变本构模型建立加速蠕变模型。

本构模型建立后需要考虑岩石损伤时的判断准则，本文采用最大拉应变准则和摩尔-库伦准则作为损伤判定准则：

$F_1\equiv -{\sigma }_3-f_{t0}=0$ 和 $F_2\equiv {\sigma }_1-{\sigma }_3\frac{1+\sin \theta }{1-\sin \theta }-f_{c0}=0$ (6)

式中 ${\sigma }_1$ 和 ${\sigma }_3$ 分别是最大主应力和最小主应力， $f_{c0}$ 和 $f_{t0}$ 分别是单元的单轴抗压和单轴抗拉强度， $\varphi$ 为内摩擦角。根据岩石的脆性特征，假定岩石在受到任何荷载条件下，拉伸损伤是优先判断的，结合公式(6)，如果细观单元满足能够满足拉伸准则，则不需要再判断该单元是否满足摩尔–库仑准则。只有未满足拉伸准则的单元，才判定其是否满足摩尔–库仑准则。

Figure 1. Elastic damage constitutive law of element under uniaxial tensile and compressive stress

图1. 细观单元单轴受拉(受压)时的弹性损伤关系

按照弹性损伤理论，单元的弹性模量按照如下关系式给出：

$E=\left(1-D\right)E_0$ (7)

式中：E和E₀分别为损伤前和损伤后的弹性模量。这里假定损伤及其演化都是各向同性的，故E、E₀和D都是标量。

细观单元在压缩和拉伸应力状态下的损伤变量D可表示为：

$D=\{\begin{array}{l}0F_1<0\text{and}{F}_2<0\\ 1-{\left|\frac{{\epsilon }_{t0}}{{\epsilon }_1}\right|}^n{F}_1=0\text{and}d{F}_1>0\\ 1-{\left|\frac{{\epsilon }_{c0}}{{\epsilon }_3}\right|}^n{F}_2=0\text{and}d{F}_2>0\end{array}$ (8)

式中 ${\epsilon }_1$ 和 ${\epsilon }_3$ 分别是最大和最小主应变； ${\epsilon }_{t0}$ 和 ${\epsilon }_{c0}$ 分别是当单元发生拉伸损伤和剪切损伤时对应的最大拉伸主应变和最大压缩主应变；n表示单元损伤演化系数，取n = 2。

3. 数值模拟

3.1. 数值模型验证

本文通过与邱贤德和杨春和已经发表的蠕变试验数据进行对比来验证所建模型的正确性 [17] [18] 。数值模型如图2所示，试样几何尺寸分别为100 mm × 50 mm和200 mm × 200 mm，类似于单轴压缩试验，模型底边在竖直方向固定，水平方向可以自由移动。为了保证验证的严格性，数值模型中的参数采用与邱贤德和杨春和论文中的岩石力学参数。弹性模量和泊松比分别为0.4 GPa、0.3和1.0 GPa、0.3。采用三角形网格划分，根据计算机的处理能力，分别划分了5024和12592个网格。

图3所示为数值模拟得到的蠕变曲线和邱贤德和杨春和得到的蠕变试验曲线。从图中可以看出模拟得到的蠕变曲线和蠕变试验曲线吻合的较一致。模拟得到了蠕变曲线的3个典型阶段，即初始、稳定和加速蠕变阶段。因此，可以说明我们提出的数值模型是正确的，可以用来研究岩石的蠕变特性。

Figure 2. Model boundary condition

图2. 模型边界条件

(a) 邱贤德的蠕变试验结果 (b) 杨春和的蠕变试验结果

Figure 3. Comparison between simulated creep curve and experimental creep curve

图3. 数值模拟蠕变曲线与试验蠕变曲线对比

3.2. 蠕变特性数值模拟

为了进一步研究岩石的蠕变特性，本文对泥岩进行了不同压力水平下的单轴和三轴蠕变数值模拟。在单轴压缩蠕变数值试验中，施加的恒定应力大小分别为10，11，12，13，14，15和16 MPa；在三轴压缩蠕变数值试验中侧压力为5 MPa，轴向压力为10，20，25，28，30，和40 MPa。

数值模型采用平面应变模型，试样尺寸为50 mm × 100 mm。如图4所示，单轴压缩蠕变数值试验中只有轴向的应力，对双轴压缩蠕变数值试验水平方向含有侧压力，模型的边界条件如图4所示。

Figure 4. Calculation model

图4. 计算模型

假定弹性模量和强度等岩石力学参数满足Weibull分布。在数值模拟前，我们进行了常规的单轴压缩强度试验，确定了岩石物理力学参数，如表1所示。

图5为单轴压缩蠕变数值模拟的岩石试样应变–时间曲线。施加的应力水平大小分别为试样瞬时单轴抗压强度的50%，55%，60%，60%，70%，75%和80%，也就是10，11，12，13，14，15和16 MPa。从图中可以看出，在加载瞬间有瞬时的弹性变形，应力水平不同瞬时弹性变形的大小也不同。加载应力水平大小对蠕变曲线有较大影响，加载应力较小时(10和11 MPa)，只出现了蠕变第一和第二阶段，岩石试件没有出现破坏。应变随着时间的增加逐渐变小，最后几乎接近于常数。对应10和11 MPa两个应力水平，应变率分别为为5 × 10⁻⁷ s⁻¹和9.5 × 10⁻⁷ s⁻¹。随着加载应力的增加，试件出现了破坏，蠕变的3个阶段也相应变得明显。

Table 1. Physico-mechanical parameters of model specimens

表1. 模型物理力学参数

Figure 5. Numerically obtained creep deformation curves under uniaxial compression creep

图5. 单轴压缩蠕变数值模拟时间–应变曲线

图6所示是加载应力为16 MPa时的损伤演化过程。损伤导致岩石弹性模量的降低，当单元完全损伤时以黑色表示，图中损伤的演化代表了裂纹的衍生过程，损伤单元以不同的颜色表示，白色和黑色分别代表剪切和拉伸破坏。

为了进一步研究岩石在不同应力状态下的蠕变特性，我们采用数值模拟进行了双轴压缩蠕变数值试验。图7所示为侧压力为5 MPa和不同轴压下的蠕变曲线。从实验结果可知，在较大的轴向压力(应力差较大)作用下，蠕变曲线的3个阶段比较明显，蠕变应变率随着时间的增加，由开始的逐渐减小到基本稳定最后发展到迅速增加。在较小的轴向应力(应力差较小)作用下，没有出现加速蠕变阶段。轴向应力增加，蠕变加快，相应的破坏时间减少。轴向应力(应力差)决定蠕变的变化快慢。

Figure 6. Failure process of rock specimen under uniaxial compression creep

图6. 单轴压缩蠕变数值模拟岩石试件破裂过程

Figure 7. Numerically obtained creep deformation curves under biaxial compression creep

图7. 双轴压缩蠕变数值模拟时间–应变曲线

4. 结论

建立了可以模拟岩石蠕变效应的数值模型，通过与已有试验数据进行对比验证了模型的正确性。并运用建立的数值模型进行了常规蠕变数值试验研究。研究结果表明，数值模拟结果和实验室试验得到的结果有较好的一致性。数值模拟得到了蠕变破裂的3个典型阶段：初始蠕变阶段、稳定蠕变阶段和加速蠕变阶段。所建立的模型适用于模拟岩石的蠕变破坏问题。轴向应力水平(应力差)对岩石蠕变有重要的影响。当施加的应力远小于屈服应力时，只有初始蠕变和稳定蠕变阶段；当施加的应力接近屈服应力时，蠕变的3个阶段都会出现。岩石的宏观蠕变破坏实质上是细观层次上单元损伤累计的结果。