1. 引言
天气概率预报初创于20世纪,但直到上世纪60年代前期为止,概率天气预报的进展比较缓慢。20世纪60年代最先由美国国家气象局把概率预报用于日常气象业务的试验;并于1965年开始在全国实施降水主观概率预报(SubpoPa)业务计划,1972年雷雨和强风暴概率预报投入业务运行,1974年短时局地强风暴概率预报系统进行试运行,1976年完成此系统的开发。20世纪70年代日本开始传送降水概率预报,并于l980年JE式对外发布东京的降水概率预报;1980年欧洲中心澳大利亚、加拿大等国和地区相继建立了降水概率预报业务系统。我国在20世纪80年代曾发布过概率预报,1995年在上海市、北京市相继发布了降水概率预报。1998年中国气象局决定在全国推行概率预报业务,但目前国内水平与美国、日本等发达国家相比还存在一定差距,不仅表现在数值预报模式的分辨率上、计算机速度上、预报产品分发处埋上,还表现在我国数值预报产品释用工作至今尚未形成完整业务。
大气自身的运动特征、数值模式的不完备、初始资料的不确定性等各类因素,促使了天气预报从从单一值的确定论向多值的概率论转变 [1] [2] 。
杜钧 [3] 、矫海燕 [4] 指出集合预报的产生和应用在一定程度上弥补了预报的不确定性,提高了预报精度,为概率预报的发展奠定了坚实的基础。Epstein [5] 提出了集合预报的思想和方法,这是一种动力随机预报方法。依据非线性理论,由于数值模式对初始状态的敏感性,集合预报方法使用多个成员来描述大气状态的不确定性,通过模式运行产生大量预报信息,可生成真正“概率论”意义下的预报结果。多模式集成方法是一种提高模式预测准确率的非常有效的后处理统计方法。多模式集成方法不仅适用于确定性预报,也可用于概率预报。其中集合概率预报可以定量评估不确定性,并且对天气变化的风险分析和决策制定提供更准确的值,从而实现经济最优化 [6] 。集合概率预报方法BMA,Raftery等 [7] 在2005年引入BMA方法,将其作为一种方法产生任何天气参数的概率密度函数。这种方法现在被广泛的用于气温、海平面气压、定量降水、风速以及风向的概率预报。贝叶斯模式平均方法(Bayesian Model Averaging,简称BMA)能够产生率定的高度集中的概率密度函数(Probability density function,简称PDF)。它对某一特定变量的概率预报是经过偏差校正的单个模式概率预报的加权平均,其权重是相应模式的后验概率,代表着每个模式在模式训练期相对的预报技巧。应用研究表明,基于BMA方法进行集合预报具有明显优势。用已有预测效果的PDF进行概率预报,这个有预测效果的PDF是经过偏差校正的各个中心的概率密度函数(PDF)的加权平均,其权重是相应模式的后验概率,代表着每个模式在模式训练阶段相对的预报技巧。
智协飞等 [8] 利用TIGGE多模式资料研究BMA方法对地面气温的10~15 d延伸期概率预报研究,结果表明BMA方法对概率预报技巧有一定的效果。智协飞等 [9] 利用多模式资料中地面气温资料进行BMA预测方法研究,结果表明,EMN的回报效果优于8个单模式的回报效果,而BMA的回报效果最好。另外,智协飞等 [10] 也比较了集合概率预报的两种不同的方法,结果发现利用BMA方法制作的概率预报的方差较小,减小了预报的不确定性,因此预报结果更接近大气的真实值。
在实际业务应用方面,如何通过有效的手段充分利用各种数值预报产品形成本地概率预报产品,十分迫切。盐城地处江苏中东部,拥有最长的海岸线和最远的沿海滩涂以及最广的海域面积,物产富饶,素有鱼米之乡的美称。冬季主要受极地变性大陆气团控制,夏季受副热带高压控制,一年四季均有灾害性天气,主要包括暴雨、大风、寒潮、高温等。本文以盐城为例,进行多模式集成将多种模式产品转化成所需的概率预报产品,进一步提升各种数值预报的客观指导价值,进一步提升本地预报水平,实现经济最优化。
2. 资料和方法
2.1. 资料
本文用包括欧洲中期天气预报中心(European Center for Medium-Range Weather Forecast, ECMWF)、美国国家环境预报中心(Global Forecast System, GFS)预报数据都是08时起报,预报未来3天96小时的2米气温。模式中心及其分辨率如表1所示。

Table 1. Basic characteristics of the two climate models
表1. 两个预报模式中心模式的基本信息
由于不同模式的分辨率不同,为便于比较,因此采用双线性插值统一将各个模式资料的2米气温统一插值到0.05˚ × 0.05˚。
本文使用Cressman插值将站点资料转换为格点资料作为观测场,与模式资料对应,格点分辨率为0.05˚ × 0.05˚。空间范围统一选取(32˚N~35˚N,119˚E~121˚E)。本文使用的2018年6~11月供6个月的气温模式在资料。
2.2. 方法
2.2.1. 贝叶斯模式平均
BMA是一种集合预报的前处理方法,可以产生有预测效果的概率预报,也可以产生确定性预报。它以实测样本隶属于某一模式的后验概率为权重,将各模式的条件概率密度函数进行加权平均,从而得到概率密度函数,其基本原理如下:
其中,
是权重,反映了第k个模式在训练期的相对贡献程度。
是非负的,且满足
。
是与单个模式回报结果
相联系的条件概率密度函数。
BMA模型的预报方差包括两项,BMA模型的预报方差包括两项,第一项是模式间的方差,反映了预报集合的离散度,第二项表示集合内的方差。
其中
分别表示格点的空间指标和时间指标,
表示第k个模式在格点
的回报结果。模式间方差反映了集合成员的离散度,模式内方差可用于衡量模式预报的不确定性。常规的概率预报方法通常只考虑了其中之一,造成了不确定性的低估。以简单集合平均为例,它仅考虑了模式间的方差,而忽略了模式内的方差,进而影响了预报效果。BMA预测了这种离散度–误差的关系,且这种关系是离散度偏小的,并可从理论上解释集合预报离散度偏低的可能性。由于模式方差也表征着预报不确定的大小,BMA方法为这种相互矛盾的现象提供了一定的理论框架,并给出了改进的方法。
2.2.2. Cressman插值
Cressman插值算法由Cressman等 [11] 在1959年提出,采用逐步订正的方法进行最优化插值,用实际资料与预备场或者初值场之差去改变和订正预备场或者初值场,得到一个新场,再求出新场与实际值之差,去订正上一次的场,直到订正后的场逼近观测记录为止。
Cressman插值算法的基本公式模型为:
其中
式中,
为任意一个气象要素(如:气温、降水等),
为变量
在格点
上的第一猜测值,
是变量
在格点
上的订正值,
为观测点k上的观测值与第一猜测值之差,
是权重因子,分别由橡胶形、椭圆形和圆形权重函数决定,在0.0~1.0之间,K是影响半径R内的台站数。
Cressman插值最重要的是权重函数
的确定,其一般形式为:
其一般取为1、2、4、7和10几个常数。
是格点
到观测点k的距离。
Cressman插值算法的基本思路如下:
S1:需要确定一个预备场,并设定一个逼近值范围,用于比较计算后的新值与实际资料的差值;
S2:计算权重
;
S3:将权重
放入插值计算中,得到一个新场;
S4:将这个新场与实际资料相比,计算他们的差是否在预定的逼近值范围内,如果不在逼近值范围内,就用这个新场与实际值的差,去订正上一次的场;
S5:对订正后的场和实际值进行比较,如果还是超过逼近值的范围,则继续订正,直到新场与实际值的差在预定的逼近值范围内。
2.3. 检验评估方法
本文采用以下三种常用的方法对BMA结果进行检验和评估。
1) 均方根误差(Root-mean-square error, RMSE),其定义为:
其中,n是训练期数据总和,
是模式回报值,
是观测值。RMSE值越小,则模式的回报效果越好。
2) 距平相关系数(Anomaly Correlation Coefficient, ACC),其定义为:
其中,n是空间场的格点样本数,
是模式回报值,
是观测值。ACC用来评估模式回报值与观测值的相似程度,因而ACC值越大,则模式的回报效果越好。
3) 连续分级概率评分(Continuous Ranked Probability Score, CRPS),其定义为:
其中,
是赫维赛德阶跃函数(Heaviside step function),如果
,
;反之,
。CRPS评分是评估概率预报效果的常用指标之一,反映了模式模拟值和观测值累计分布函数的区别,因而CRPS取值越小,则模式的模拟效果越好。
3. 检验评估
对多模式进行集合预报,并采用ACC、RMSE、预报误差1℃和2℃的预报准确率以及CRPS,对多模式集成结果进行气温预报效果评估。图1~4就是各个指标的评估效果。从ACC、RMSE以及预报误差在1℃和2℃的预报准确率可以看出大部分预报时效内,BMA的确定性结果都具有较好的预报效果。就从ACC来看,预报技巧最大幅度可以提高0.12,但随着预报时效的增大,提高的幅度逐渐减小。从RMSE来看,大部分预报时效预报技巧有提高,最高可以减少2.7℃,并且同样,随着预报时效逐渐变大,预报技巧提高幅度逐渐减小。对于地面气温预报误差在1℃的准确率最高可提高0.13,预报误差在2℃的准确率最高可提高0.13。
CRPS可以看出在所有预报时效内,BMA的预报技巧都高于其他两个模式,最高技巧提高幅度可达0.4,并且随着预报时效的增长,预报的技巧提高幅度逐渐减小。另外,对于所有时效,CRPS值还是比较大。说明各个模式以及BMA方法对盐城区域范围内2米气温预报仍存在一定的困难。也说明对盐城区域的气温的预报研究存在一定的实际意义。
4. BMA概率预报结果
4.1. 单点预报结果
对研究时段内但各个点的地面2 m气温进行BMA预报研究。图5给出格点(32˚N, 119.45˚E) 00~96 h预报期内的5%、25%、50%、75%、95%的概率折线图。对于大部分预报时效而言,观测值接近于50%的概率值附近,说明BMA方法预测出的预报值是最大概率值。
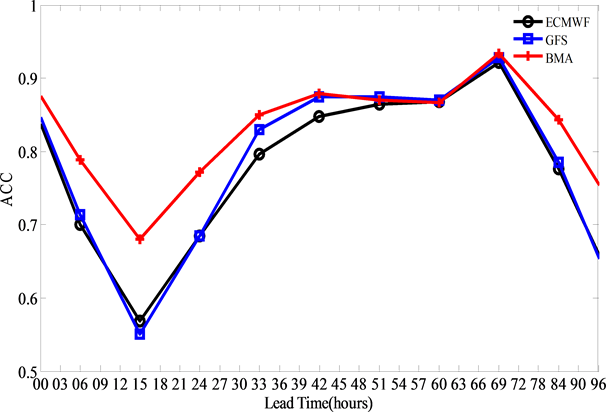
Figure 1. The variation of ACC with 96 h leading time at 08:00 for T2m by different model (ECMWF, GFS) and BMA
图1. 单模式(ECMWF, GFS)和BMA对T2m变量08:00时起报的96 h时效的预报期平均ACC

Figure 2. The variation of RMSE with 96 h leading time at 08:00 for T2m by different model (ECMWF, GFS) and BMA (unit: ˚C)
图2. 单模式(ECMWF, GFS)和BMA对T2m变量08:00时起报的96 h时效的预报期平均RMSE(单位:℃)
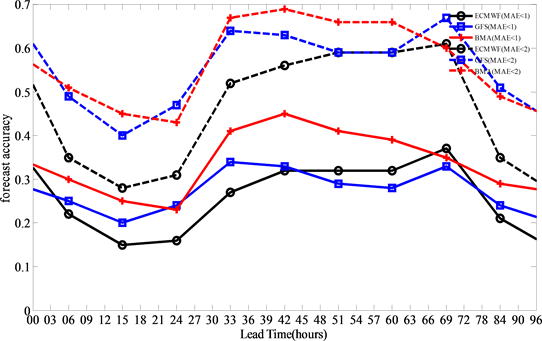
Figure 3. The variation of forecast accuracy of 1˚C and 2˚C with 96 h leading time at 08:00 for T2m by different model (ECMWF, GFS) and BMA
图3. 单模式(ECMWF, GFS)和BMA对T2m变量08:00时起报的96 h时效的预报期误差1℃和2℃的平均预报准确率

Figure 4. The variation if CRPS with 96 h leading time at 08:00 for T2m by different model (ECMWF, GFS) and BMA
图4. 单模式(ECMWF, GFS)和BMA对T2m变量08:00时起报的96 h时效的预报期平均CRPS
4.2. 区域预报结果特征
图6对预报期的2米最高气温作为预报值,可以看出其概率分布多集中在80%附近,即对于本次试验而言,80%的概率值下的温度可作为高温天气的预警。这对于高温预警具有一定的参考价值,也同样可以为用户和决策者提供这种预报结果的不确定量值。相应地,将该方法可应用于所需预报时段,不仅可以给出最高气温的阈值范围也可以给出最高气温发生概率的地理分布情况。图7地面2米的气温观测值的概率值分布,可以看出观测值更接近于40%概率,因此除了BMA提供的确定性预报之外,可以就
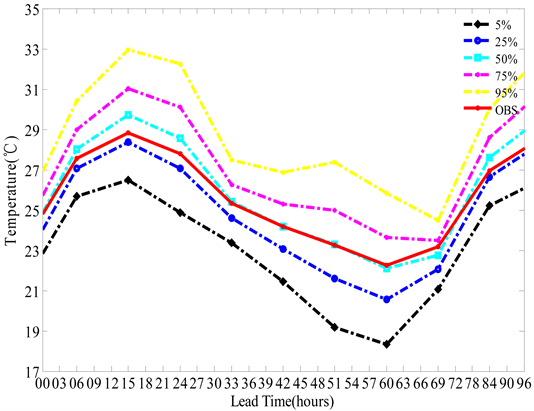
Figure 5. Surface air temperature of different probability (5%, 25%, 50%, 75%, 95%) in 00 - 96 h at the grid point (32˚N, 119.45˚E), the dotted curves are the BMA predictive, dashed curve is observation
图5. 格点(32˚N, 119.45˚E) 00~96 h预报期内的5%、25%、50%、75%、95%的概率分布,虚线是BMA预报值,实线是观测值
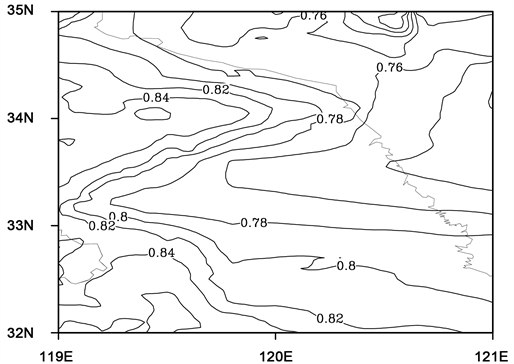
Figure 6. The spatial probability distribution of the observed maximum surface air temperature with a lead time of 000
图6. 地面气温预报时效000对应时效最高气温的概率分布
各地分布情况,将不同概率下的预报值作为温度预报的参考值。图8给出了气温概率分布的空间分布特征,给出不同概率下的温度分布(5%, 50%, 75%, 95%),从低概率到高概率,可以清晰看出,温度随着的概率的增加而升高。陆地和海洋相比,陆地温度的上升幅度会比较大,这与海陆热力性质的差异有很大关系。

Figure 7. The spatial probability distribution of the observed surface air temperature with a lead time of 000
图7. 预报时效000对应时效地面气温观测值的概率分布
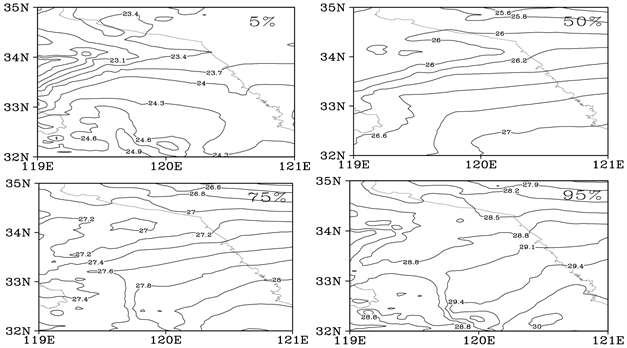
Figure 8. The spatial distribution of surface air temperature in probability of 5% - 95% in leading time 000 at 08:00
图8. 地面气温08时起报000预报时效下不同概率下(5%~95%)的温度分布
5. 总结
本文利用ECMWF、GFS两个模式的BMA预报结果进行2米气温0~96 h的概率预报研究,得到以下几个结论:
1) BMA方法对于0~96 h预报时效不仅可以提供确定性结果也可以做出概率预报,对于确定性结果,ACC、RMSE、误差在1℃和2℃的预报准确率而言,预报技巧都有提高。对于概率预报,CRPS预报技巧都有提高。
2) BMA提供的确定性预报结果可在实际精细化预报中发挥作用。
3) BMA概率预报,提供的80%概率下的预报值可作为最高气温的预警。这对于夏季高温预警有很好的警示作用。