1. 引言
在英国石油公司(British Petroleum) 2018年的世界能源统计年鉴 [1] 中,可以看到2017中国能源消费增长3.1%,目前中国仍然是世界上最大的能源消费国,占全球能源消费量的23.2%和全球能源消费增长的33.6%。尽管煤炭仍是中国能源消费中的主要燃料,但2017年其占比为60.4%,创历史新低。中国可再生能源消费增长31%,占全球增长的36.0%。中国可再生能源消费占全球总量的21.9%。在非化石能源中,中国太阳能消费增长最快,达76%,其次是生物质能,增长达25%,风能增长达21%,水电增长达0.5%。在能源的研究中,其分为一次能源和二次能源。一次能源是指自然界中以原有形式存在的、未经加工转换的能量资料,又称天然能源,如煤炭、石油、天然气、水能。目前中国已经是世界上第一大的能源消费国,但在科技进步和环境需求的共同驱动下,能源的结构正在向更清洁、更低碳的燃料转型。于是,对中国能源的消费研究是很有意义的工作,研究的结果不仅对能源的消费有更清晰的认识,也能为政策的制定提供可量化的科学依据。
在对数据预测分析中,指数曲线 [2] 是很重要且常见的一类预测模型,其主要描述的是各期的环比增长速度相同,或者时间序列的逐期趋势按一定的百分比递增或递减。2010年,秦尚林等 [3] 利用指数曲线拟合的方法对武广铁路专线的路基沉降进行了分析。刘芳等 [4] 于2013年将分段指数模型应用于风电功率的预测研究中,并取得了很好的结果。杨桂元 [5] 根据指数曲线预测模型的特点,对指数曲线预测模型的假设、参数估计、拟合误差及无偏性等若干问题进行了探讨。进一步,在经典的指数曲线的基础上增加一个常数项,即为修正的指数曲线 [2] 。它主要描述如某种刚问世的新产品,初期销售量增长可能很快,当市场拥有量接近饱和时,销售量逐渐趋于某一稳定的水平。李晓风 [6] 应用修正指数曲线模型对我国的人口未来发展情况进行了短期的预测。王吉权 [7] 在现有文献的基础上,给出了修正指数曲线参数估计的另一种新方法,并将其应用在电力负荷预测研究中。欧阳明等 [8] 构造了一个新的修正指数曲线模型,并以单桩静载荷试验数据进行拟合。计算结果表面修正的指数曲线比双曲线模型和指数模型都要好。石文杰 [9] 使用修正指数法来对某高速公路施工之后的软土路基的沉降问题进行了预测。
振荡序列预测问题是现实世界里广泛存在的一类比较复杂的问题,如能源消费与需求、应急资源需求预测、新产品销售预测等。在上述文献和文献 [10] 的综合启发下,本文提出一种新型的振荡型的指数曲线模型。结合最小二乘法和科学计算软件,给出了模型参数的计算方法和详细过程。最后将其应用在一次能源消费的预测上,并将计算结果与传统的指数模型、修正的指数模型进行对比。从数值结果上可以看出,本文提出的模型在一次能源预测上有更高的精度。
2. 指数曲线和修正的指数曲线
2.1. 指数曲线
由文献 [2] ,经典的指数曲线为
。 (1)
为了估计参数
,在手工计算中,一般首先将两端取对数,得
。 (2)
然后运用最小二乘法和方程(2),得到如下方程
,(3)
估计出参数
和
,再取反对数,即可得到参数
、
的估计值。
2.2. 修正指数曲线
在经典指数曲线的基础上增加一个常数
,即得到修正指数曲线方程
, (4)
其中,
、
、
为未知参数, ,
,
。
,
,
。
参数
、
、
估计的基本思想是三和法:把整个时间序列分成相等的三个数组,每个组有
项,根据趋势值
的三个局部总和分别等于原数列观察值
的三个局部总和来确定三个参数。具体为:设观察值的三个局部总和分别为
、
、
,得
,
,
。 (5)
由三和法得到如下方程
。 (6)
通过方程(6)解得
。 (7)
3. 振荡型的指数曲线
在上面指数模型的基础上,本文提出振荡型的新型指数曲线,其一般方程为
,(8)
相比于经典的指数模型和修正的模型,最大的一点是引入
部分以描述系统行为对序列的振荡性影响。但是,振荡型指数曲线带有5个未知参数,且方程(8)本身为非线性函数。所以,在对参数的估计时采用的是最小二乘法。
令原始序列为
。取序列前面的
个数据来求解最优的系统参数
。事实上,将得到的最优参数带入方程(8)有
(9)
为此,构造如下的最优化目标函数
。(10)
利用高等数学中多元函数极值问题的求解思路,对方程(10)关于系统参数求一阶导数,可得到如下的方程组
(11)
对于方程(11),求解系统参数的解析解几乎是一件不可能的事情。基于此,我们借助数值计算方法的Levenberg-Marquardt算法进行求解。一旦得到系统最优参数的取值,则可用模型对具体的序列进行建模、预测分析。在上述求解中,关于m值的选取并没有统一的标准,一般根据所建立的优化目标函数来确定。对于不同的问题,不同的优化目标函数,m值的选取是不一样的,但总的原则就是使目标函数达到最小值。
4. 应用实例
为了对新型振荡型的指数曲线的预测精度和拟合效果进行检验,本文选用实际数据来验证分析,并将计算结果与已有的指数曲线、修正的指数曲线模型的计算结果进行对比分析。本文选取中国一次能源消费2004年至2017的统计数据进行分析,数据见文献 [1] (表1)。
为了检验模型的预测精度,根据预测值与实际值确定绝对百分误差(APE)和平均绝对百分误差(MAPE)如下。

Table 1. The statistical data of the primary energy consumption of China (mtoe)
表1. 我国一次能源消费量的统计数据(百万吨油当量)
, (12)
。(13)
从表达式(13)可知,当
,MAPE为拟合误差,记为
;当
,MAPE为预测误差,记为
;当
,MAPE为总误差,记为
。
本文结合MATLAB编程软件,使用2004年至2013年共10年的我国一次能源消费统计数据对其进行模型拟合。以2014年至2017年共4年的数据为模型外推预测检验数据。使用指数曲线模型、修正的指数曲线模型、振荡型的指数曲线模型进行拟合建模和外推预测,并将计算结果进行对比分析。上述三种模型的数值计算结果见表2。相应的图形分别见图1、图2和图3。
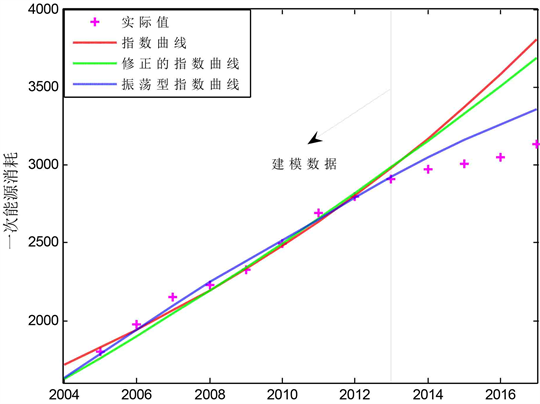
Figure 1. Modelling and forecasting the primary energy consumption by the exponential curve, the modified exponential curve and the oscillation exponential curve models
图1. 指数曲线、修正的指数曲线和振荡型的指数曲线对一次能源消费的拟合预测

Table 2. The results of China’s primary energy consumption by the exponential curve, the modified exponential curve and the oscillation exponential curve models
表2. 指数曲线、修正的指数曲线和振荡型的指数曲线对一次能源消费的计算结果
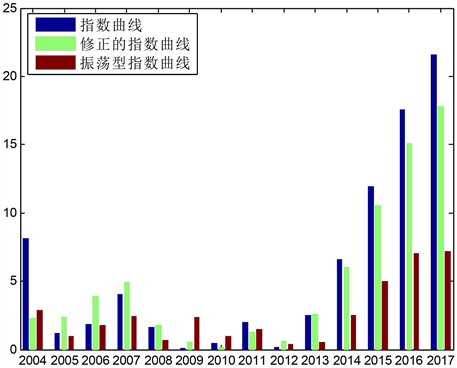
Figure 2. The absolute percentage errors of the primary energy consumption by the exponential curve, the modified exponential curve and the oscillation exponential curve models
图2. 指数曲线、修正的指数曲线和振荡型的指数曲线对一次能源消费的绝对百分误差
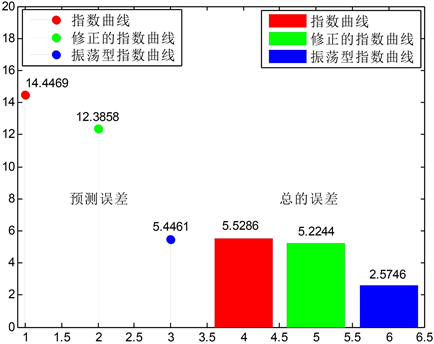
Figure 3. The forecasting error and the total error of the primary energy consumption by the exponential curve, the modified exponential curve and the oscillation exponential curve models
图3. 指数曲线、修正的指数曲线和振荡型的指数曲线对一次能源消费的预测误差和总误差
5. 结论
本文在传统的指数曲线基础上,引入振荡型来描述现实世界的振荡序列。通过最小二乘法构建最优目标函数来求解系统的各个参数的取值,并进一步将其应用在我国一次能源消耗的拟合预测中。新型振荡型的指数曲线模型预测精度高于指数曲线和修正指数曲线模型。本文所建立的新型振荡型的指数曲线模型计算简单,计算量小,可进一步考虑应用于其它能源、教育、经济等方面。