1. 引言
1994年,Dickey等人在《科学》杂志上发表论文,表明月亮远离地球的速度是每年3.82 ± 0.07厘米 [1] 。
月亮为什么远离地球?一般的学术、科普以及新闻解释是潮汐原因 [2] - [9] 。早在公元前三世纪,一些观星家就曾发现地球正在逐渐远离太阳。随着科学技术的进步,科学家们进一步测得地球与太阳之间的距离每年都会增加1.5厘米 [10] 。关于地球逐渐远离太阳的原因,科学家们长期以来一直争议不断。其中一个说法就是太阳正在通过核聚变和太阳风的方式失去其足够质量 [11] [12],而导致其引力逐渐减弱。另外的说法是潮汐作用 [13] 。
综上所述,月亮远离地球,地球远离太阳的原因是潮汐作用,而地球远离太阳多了一个太阳质量的损失原因。
潮汐作用看似是一个普遍的解释,因为既可以解释月亮远离地球,又可以解释地球远离太阳,但是,当我们把潮汐作用扩展到整个太阳系内行星远离太阳的时候,发现有些行星没有潮汐作用,比如火星,这就遇到了麻烦。而用太阳质量损失虽然可以解释八大行星的远离,但是,却不能解释月亮为什么远离地球,所以,这两种解释还不能算是一种在本质上的统一解释。
下面我们尝试用时空阶梯理论解释,尽量包括八大行星和月亮在内,发现一个统一的合理解释。
2. 时空阶梯理论简介
时空阶梯理论通过对比研究 [14],发现电是能量的压缩版,而磁场是中医气的压缩版,所以,对比电与磁,得出能量与中医气的结论就是:随时间变化的气场可以激发涡旋能量场,随时间变化的能量场可以激发涡旋气场,能量场和气场不是彼此孤立的,它们相互联系、相互激发组成一个统一的能量–气场。能量场的概念来自类比研究中的高斯定律(描述电场是怎样由电荷生成),所以,相应的能量场的描述为:能量线开始于能量收缩态,终止于能量膨胀态。从估算穿过某给定闭曲面的能量场线数量,即能量通量,可以得知包含在这闭曲面内的总能量。更详细地说,穿过任意闭曲面的能量通量与这闭曲面内的能量极化数量之间的关系。而时空阶梯理论进一步的解释是:能量场开始于能量收缩态,就是原子核状态,终止于能量膨胀态,而能量最大的膨胀态就是暗能量,而暗能量和原子核,在时空阶梯理论看来,就是形而上时空与形而下时空的一对矛盾统一体。之所以说是矛盾统一体,就是形而上时空暗能量是膨胀的,形而下时空原子核是收缩的,而且,暗能量膨胀的原因就是原子核的收缩,原子核收缩的原因就是暗能量的膨胀。能量场,开始于原子核的收缩态,终止于暗能量的膨胀态,说明,原子核和暗能量是一个统一体,都在能量场内。
气场的概念来自类比研究中的高斯磁定律(磁场的散度等于零),所以,相应的气场的描述为:由能量产生的气场是被一种称为偶极子的位形所生成。气偶极子最好是用能量流回路来表示。气偶极子好似不可分割地被束缚在一起的正气荷和负气荷,其净气荷为零。气场线没有初始点,也没有终止点。气场线会形成循环或延伸至无穷远。换句话说,进入任何区域的气场线,也必须从那区域离开。通过任意闭曲面的气通量等于零,气场是一个螺线矢量场 [14] 。
既然有了以上的能量场和气场的概念,下面我们就通过对比研究来发现更多的东西:
在电动力学里,洛伦兹力(Lorentz force)是运动于电磁场的带电粒子所受的力。根据洛伦兹力定律,洛伦兹力可以用方程,称为洛伦兹力方程,表达为:
其中,
是洛伦兹力,q是带电粒子的电荷量,
是电场强度,
是带电粒子的速度,B是磁感应强度。
洛伦兹力定律是一个基本公理,不是从别的理论推导出来的定律,而是由多次重复完成的实验所得到的同样的结果。
既然能量场类似电场,气场类似磁场,类似地,我们可以得到能量气场力方程,表达为:
其中,F是能量气场力,m是星体质量,E是能量场强度,v是星体的速度,Q是气感应强度。
在宇宙学研究中,哈勃定律成为宇宙膨胀理论的基础,以方程表示:
其中,
是由红移现象测得的星系远离速率,
是哈勃常数,D是星系与观察者之间的距离。
而能气场理论有:
其中,
是星体的运行速度,而Q是气感应强度,R是星体距离星系中心的距离。
对比
与
,发现唯一的区别就是
中有
项,假如星体运行方向与气场
垂直,
,那么,两个公式就完全相同。所以,哈勃常数对应的是能气场中的气感应强度(或者叫做气场强度也可以,因为这里没有历史的冲突问题。也就是说,气场强度和气感应强度是同一个指标)。
这样,我们就知道了暗能量或者宇宙膨胀原来与气场强度(气感应强度)有关。
我们以能量场为基础,计算出三个星系自转曲线的理论值,这些理论值与实际观测数值基本吻合。我们以气场理论为基础,把哈勃常数作为气场强度的对应值,计算出了先驱者号异常加速度的理论值,与之前的实际计算基本吻合。
这里的关键是,暗物质和暗能量的计算,来自同一理论基础,就是能气场理论,而两者的计算理论值与实际观测值都基本吻合,这证明能气场理论是正确的 [14] 。
3. 按照哈勃定律计算
我们首先按照哈勃定律计算月亮远离地球的距离,以及八大行星远离太阳的距离。
详细计算:
,v是月亮远离地球的速度,H是哈勃常数,而D是月亮到地球的距离,计算得到V = QD = 8.7935567e−10 m/s,一年远离0.0277313605米,就是2.77313605 cm,而测量得到月亮远离地球的距离是每年3.82 ± 0.07 cm [1],虽然不等,但是相差不多,感觉有些对。但是,接下来的计算就有些问题了,下面是按照哈勃定律公式计算得到的每年八大行星远离太阳的距离(按照
计算,D是行星的平均轨道半径) (表1)。

Table 1. The theoretical calculation distance of the eight planets away from the sun
表1. 八大行星远离太阳的理论计算距离
而实际观测的远离距离是表2 [11] 。

Table 2. The actual observation distance of the eight planets away from the sun
表2. 八大行星远离太阳的实际观测距离
对比表1的理论计算数值和表2的实际观测数值相差很多,初步断定,用哈勃定律算不出行星膨胀的距离。
4. 经验公式的建立
以上按照哈勃定律计算不出行星膨胀的距离,我们需要考虑形而下时空的收缩影响,或者说,行星或者卫星的膨胀速度需要乘以与膨胀有关的系数。
首先想到的公式就是类似哈勃定律的公式,但是,这里的哈勃常数改为气感应强度,因为时空阶梯理论揭示,哈勃常数对应气感应强度 [14],所以最先想到的公式如下:
v是行星(地球等)膨胀的速度,或者卫星(月亮等)膨胀的速度,Q是气感应强度,D是行星到太阳的距离,或者月亮到地球的距离。
膨胀速度由于受到引力收缩的影响,肯定缩小了,而想达到哈勃定律那样的速度,就需要乘以一个膨胀系数,而时空阶梯理论的基础就是宇宙以等角螺线的方式膨胀,所以,行星膨胀的速度乘以一个等角螺线的膨胀系数,就等于哈勃定律中的天体退行速度
(
),而气感应强度与哈勃常数相差一
个时空阶梯因子
(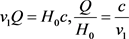 [14] ),所以乘以一个时空阶梯因子,就与哈勃定律中的
[14] ),所以乘以一个时空阶梯因子,就与哈勃定律中的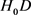 相当了。
相当了。
所以,最后得到的经验公式是:
又因为:
宇宙收缩加速度(
) = 宇宙膨胀加速度(
) [14],
所以最终的经验公式是:
这里的k1是膨胀系数(以等角螺线的方式膨胀),v是行星(地球)膨胀的速度,或者卫星(月亮)膨胀的速度,H0是哈勃常数,D是行星到太阳的距离,或者月亮到地球的距离。V1是行星或者月亮的轨道运行速度,c是光速。
哈勃常数有两个数值,一个来自欧洲空间局发射的普朗克探测卫星,2015年测量宇宙微波背景辐射,结果得出:哈勃常数为67.74 ± 0.46公里/秒∙百万秒差距(67.74 ± 0.46 km/s/Mpc)。另外一个是诺奖得主研究团队最新研究成果:73.45 ± 1.66公里/秒∙百万秒差距(73.45 ± 1.66 km/s/Mpc) [15] 。
计算得到哈勃常数平均值为:H0 = 70.595 km/s/Mpc = 70595 m/s/3.086e + 22 m = 2.28758911212 × 10−18/s。
月亮到地球的平均距离 = 384,403,900米,月亮的公转速度 = 1022 m/s,光速 = 299,792,458 m/s。
月亮膨胀的速度是 = 3.82 cm/年 [1] 。
代入各个数值算出膨胀系数是:K1 = 62466714487.987724 = 499.93341567673994。
为了容易计算,我们把膨胀系数改为K的四次方,所以公式改为:
而相应的膨胀系数就是:k = 499.9334156767399。
5. 验证经验公式
有了行星或者卫星的膨胀速度公式,我们可以验证各个行星的膨胀速度了。首先我们收集整理八大行星到太阳的平均距离和轨道平均速度(表3),然后逐一计算。

Table 3. Average distance from the eight planets to the sun and average orbital speed
表3. 八大行星到太阳的平均距离和轨道平均速度
八大行星只用一个膨胀系数k = 499.9334156767399 (月亮的膨胀系数),计算得到理论远离距离,我们可以从表4中看到,只有金星和地球的理论计算值和实际观测值比较接近。但是,这个结果,已经初步
判定,经验公式
适合月亮和地球,以及金星。但是,这个结果远远不够。我们需要发现膨胀系数的等角螺线公式,以便适合每一个行星。

Table 4. Distance of eight planets away from the sun calculated using only one expansion coefficient
表4. 八大行星只用一个膨胀系数计算得到的远离距离
我们按照八大行星的实际远离距离,算出八大行星的膨胀系数如下(表5)。

Table 5. Expansion coefficient calculated according to the actual distance
表5. 按照实际测量远离距离算出的膨胀系数
我们以地球的实际膨胀系数为基础,不难找到膨胀系数的等角螺旋公式如下:
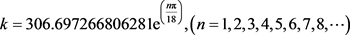
我们用这个膨胀系数的等角螺线公式计算理论膨胀系数,再与实际观测的膨胀系数对比(表6)。

Table 6. Comparison between theoretical expansion coefficient and actual expansion coefficient
表6. 理论膨胀系数与实际膨胀系数的对比
通过以上对比,我们发现,找到的膨胀系数螺线公式计算的膨胀系数与实际膨胀系数接近。
下面我们看看,以膨胀系数的螺线公式计算的远离距离与实际距离的差别(表7)。


Table 7. The difference between theory and actual distance
表7. 理论与实际远离距离的差别
以八大行星为标准,月亮的膨胀系数按照地球的膨胀系数(517.7331396)计算,得到的理论远离距离是:0.033211475349796515 m,而观测距离是0.0382 m [1],理论计算与实际观测相差0.004988525 m。
我们看到,理论计算的远离距离与实际观测的远离距离,已经非常接近了。
说明,经验公式:
已经适合太阳系的八大行星以及月亮了。
假如这个经验公式,可以算出木星卫星的远离距离,就更加证明这个经验公式适合太阳系的行星和卫星。
最后需要强调的是,虽然观测值与理论计算值接近,但是,差别还是有的,这个差别的产生,有两方面的原因,一个是理论计算方面有缺陷,需要改进,另外一个是实际观测不是太准确,有误差。另外,月亮远离地球的距离,按照地球的膨胀系数,计算的理论值小于观测值,这为潮汐作用的解释留有了空间。所以,时空阶梯理论的解释,尤其在月亮远离地球的原因上,不排斥潮汐作用的解释,也许,月亮远离地球的最终原因就是潮汐和宇宙膨胀两大原因。
6. 对经验公式的初步解释
建立了经验公式,初步验证实际膨胀距离与理论计算距离接近,但是,这个经验公式有什么意义吗?这个经验公式为什么是这个形式。我们需要研究明白。
我们把这个经验公式变换一下:把
变为
,这里的
是哈勃定律中的天体膨胀速度,而v是太阳系行星的膨胀速度,k是太阳系的膨胀系数。
在时空阶梯理论中,
是时空阶梯因子,有了这个因子,我们可以把所有的力综合起来,
[14],所以,它是时空阶梯因子,也是力的时空阶梯因子。
进一步研究发现,时空阶梯因子的倒数
原来与精细结构常数类似,事实上,精细结构常数的数值
就是基态轨道上电子的线速度与光速之比。而v1是行星的轨道运行速度,与电子在原子内的运行类似。精细结构常数是电磁相互作用中电荷之间耦合强度的一种度量,或者说,它就是电磁相互作用的强度。说到底,原来精细结构常数与电磁力的收缩力的大小程度有关,按照时空阶梯理论的理解,就是与形而下时空收缩程度有关,具体说就是与电磁力时空的收缩程度有关。而时空阶梯理论通过对比研究,发现
电是能量的压缩版,而磁场是中医气的压缩版,所以,到了这里,时空阶梯因子的倒数
成了太阳系内
的类似原子的精细结构常数。那么这个类似原子的太阳系精细结构常数的意义就是能气相互作用的强度,就是能气场力 [14] 收缩程度的一个量。
为什么是平方?相对应的电磁理论在这里:在索末斐模型中,不同角量子数的轨道之间的能级差正比于精细结构常数的平方 [16] 。
在量子电动力学中,任何电磁现象都可以用精细结构常数的幂级数来表达,精细结构常数被叫做耦
合相互作用常数。我们以此推测,太阳系内的能气现象都可以与太阳系内的时空阶梯因子
的等角螺线的膨胀系数倍数来表达。
通过对比研究,我们终于明白
是一个太阳系内能气场收缩程度的一个度量,公式
的意思是说,哈勃定律中天体的膨胀速度,消除了太阳系内的能气场收缩的影响,就是太阳系行星的膨胀速度。
一句话,太阳系内行星的膨胀速度,受到能气场收缩的制约,所以膨胀速度小于哈勃定律中星体的膨胀速度。
到了这里,我们终于看清楚,其实,哈勃定律是经验定律,需要增加能气场力对这个定律的修正。我们计算太阳系内行星的膨胀速度,就算是对哈勃定律的一种修正。至于像银河系或者更大的天体的计算,需要不断积累数据才能做到。
最后需要说明的是,K为什么叫膨胀系数,而不叫收缩系数?是因为在时空阶梯看来,形而下时空的收缩与形而上时空的膨胀是对等的,因为我们要研究行星的膨胀速度,所以就用了膨胀系数。事实上,形而下时空的收缩也是以等角螺线的方式收缩的,就是改用收缩系数,也是一样的公式和结果。
7. 精细结构常数的意义
既然太阳系内也有一个类似原子内的精细结构常数,我们就需要把精细结构常数的意义研究清楚。
精细结构常数是物理学重要的无量纲量,常用希腊字母
表示,精细结构指的是原子物理学中原子谱线分裂的样式。其定义为
,
或者:
其中:
e是基本电荷,
是真空电容率,
是约化普朗克常数,是普朗克常数,
c是光速。
精细结构常数,人们对它物理含义的第一个解释就是玻尔模型中处于基态的电子运动速度与光速的比值。然而随着量子力学的发展,薛定谔方程建立起来,人们开始用电子云和几率描述核外电子,抛弃了电子具有经典理论中确定的轨道和速度的概念。狄拉克把量子波动力学与相对论相结合,提出电子的相对论性量子力学方程——狄拉克方程。狄拉克方程认为光谱的精细结构是由电子的自旋–轨道作用引起的,是一种相对论效应。量子电动力学认为,精细结构常数是电磁相互作用中电荷之间耦合强度的度量,表征了电磁相互作用的强度。
通过以上介绍,我们知道原子的精细结构常数,是表征电磁相互作用的强度。假如精细结构常数变大了,就说明电磁相互作用的强度变大了,相对应的就是原子收缩了。
原子内
,太阳系内
,按照时空阶梯理论,宇宙膨胀,原子收缩,所以,
中的v变大了,就说明电子更靠近原子核了,原子的确是变小了,收缩了。而太阳系中的精细结构常数
,因为行星膨胀了,行星的轨道速度变慢了,所以,太阳系中的精细结构常数
变小了。时空阶梯理论揭示 [14],形而下时空原子收缩,形而上时空宇宙膨胀,是宇宙演化的两极,而太阳系虽然是属于形而下时空,但是,由于太阳系偏向整体宇宙的膨胀一端,所以太阳系还是偏向膨胀。从具体太阳系的变化,我们现在可以正确区分什么是形而下时空,什么是形而上时空了。形而下时空就是物质和暗物质时空,而形而上时空就是暗能量时空,从光速不变这个宇宙标尺来讲,等于和小于光速的时空都是形而下时空,大于光速的时空是形而上时空。大于光速的形而上时空是膨胀时空,所以太阳系的膨胀,其实是太阳系内形而上时空的膨胀,而具体的物质时空,太阳,地球还是偏向收缩的。
也就是说,太阳系和原子都含有形而上时空和形而下时空,形而上时空膨胀,形而下时空收缩,是两个相反相成的时空在同时运动,这个两个同时运动的时空,会对对原子内的电子和太阳系中的行星有不同的作用。在原子内,形而下时空的收缩和形而上时空的膨胀都很强,所以,原子内的电子虽然属于形而下时空,但是在强大的形而上时空膨胀的作用下,看似粒子的电子其实更像电子云,这个电子云在形而上时空膨胀强的时候,就像蒸发一样,进入了形而上时空,而在形而下时空收缩很强的时候,就像冷凝一样,进入形而下时空。所以,电子云就像地球的云彩一样,在天空和地面来回转换,一会是云,一会是雨。由于过去我们对于形而上时空一无所知,所以,就感觉量子力学有些怪异。其实,太阳系的形成,也是通过最早的原始太阳系星云开始的,有形而下时空的收缩,也有形而上时空的膨胀。形而下时空的收缩,逐渐形成太阳和八大行星,而其中的空间距离的增大其实就是形而上时空的膨胀。严格说起来,地球上水–云–雨–水的循环变化,其实也是形而上时空膨胀和形而下时空收缩导致的复杂运动变化。
有了以上说明,我们就不难理解这句话“然而随着量子力学的发展,薛定谔方程建立起来,人们开始用电子云和几率描述核外电子,抛弃了电子具有经典理论中确定的轨道和速度的概念”的具体含义了。薛定谔方程的革命意义,就是把形而上时空加入了方程,因为薛定谔方程不同于普通的波动方程的地方就是时空波动速度u,这速度u是相速度,而不是粒子的移动速度v [14] 。根据时空阶梯理论,相速度是形而上时空的速度。可见,薛定谔方程是形而上时空的波动方程。有了形而上时空的膨胀,就有了电子云,而电子云类似地球的云彩,在什么地方落雨,具有一定的概率,所以,对于波函数一直存在着德布罗意与薛定谔等人的实在论解释与玻恩等人的概率解释 [17] 。其实,两种解释都对,实在论的解释是从形而下时空看的,概率解释是从形而上时空看的。将来有一天,我们对于形而上时空的了解类似现代气象学对于地球天空的了解的时候,我们就不会对于量子现象感到有些诡异了。其实,古代人对于天气变化的困惑理解,就是我们对于量子力学的困惑理解,两者有本质上的相似性,就是古代人对于地球整体天空的了解很匮乏,而现在我们对于形而上时空的了解很匮乏。
“狄拉克方程认为光谱的精细结构是由电子的自旋–轨道作用引起的,是一种相对论效应”。相对论效应,在时空阶梯理论看来,就是给形而下时空一个划了一个界限,就是光速和光速以下的是形而下时空,形而下时空不可能超光速,而且形而下时空是收缩的,收缩是是逐渐增强的。狄拉克方程具有更丰富的形而下时空阶梯的内容,所以,狄拉克方程可以描述更丰富的粒子和粒子的自旋 [14] 。
这里,为什么用如此大的篇幅讨论这个问题,就是因为这是量子力学的最难理解的地方,这里用水–云–雨–水的比喻来形容电子云是最贴切的,其实,地球上的水–云–雨–水的循环变化就是类似电子云的变化。而天气预报的概率也印证着玻恩等人的概率解释其实是对的。当然,最诡异的地方是电子云可以蒸发为形而上时空,而形而上时空的速度是超光速,一切超光速的电子纠缠现象都是在形而上时空内完成相互联系的,时空阶梯理论揭示,形而下电磁力时空对应的形而上虚时空的波动速度是: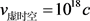 ,而一个普朗克长度的波弦,在一秒之中,以速度
可以形成整个宇宙(c是光速) [14],我们可以看到,
大
太多,所以,以量子纠缠的速度到达整个宇宙之内的任何地方几乎是毫无延迟的。但是,当这些形而上时空的电子云下降为粒子电子的时候,速度是小于光速的,而这些形而下时空电子现象倒是容易理解的。所以,最难理解的地方就是形而上时空方面,也就是暗能量方面,这将是未来研究的重点。我们相信,一旦我们进入形而上时空的研究,一切难以理解的量子力学的诡异现象都将烟消云散。
,而一个普朗克长度的波弦,在一秒之中,以速度
可以形成整个宇宙(c是光速) [14],我们可以看到,
大
太多,所以,以量子纠缠的速度到达整个宇宙之内的任何地方几乎是毫无延迟的。但是,当这些形而上时空的电子云下降为粒子电子的时候,速度是小于光速的,而这些形而下时空电子现象倒是容易理解的。所以,最难理解的地方就是形而上时空方面,也就是暗能量方面,这将是未来研究的重点。我们相信,一旦我们进入形而上时空的研究,一切难以理解的量子力学的诡异现象都将烟消云散。
量子电动力学认为,精细结构常数是电磁相互作用中电荷之间耦合强度的度量,表征了电磁相互作用的强度。量子电动力学把形而下时空的收缩发展到极致,以精细结构常数为基础,发展出耦合常数,而耦合常数把形而下时空的四种收缩力统一起来,就是形而下时空收缩有一个阶梯,这个阶梯最弱的就是牛顿引力,而最强的就是强相互作用力。在这个意义上讲,时空阶梯理论的力的总公式
与量子电动力学的力的解释等效,都是以精细结构常数为基础。
通过以上描述,我们现在知道,精细结构常数的意义,就是形而下时空收缩的一个重要指标。但是,在时空阶梯看来,精细结构常数的意义,除了以上意义,还有宇宙膨胀与否的意义。时空阶梯理论的核心就是原子收缩,宇宙膨胀,原子膨胀,宇宙收缩。现在证明,原子的精细结构常数在变大 [18] [19] [20],说明原子在收缩,而按照时空阶梯理论,原子收缩,那么,宇宙就膨胀,而现在的天文观测也证明宇宙正在膨胀 [21] [22],所以,时空阶梯理论的核心被证明是正确的。
下面我们总结一下精细结构常数的宇宙意义:
1) 原子的精细结构常数变大,说明宇宙膨胀。
2) 原子的精细结构常数变小,说明宇宙收缩。
3) 原子的精细结构常数不变,说明宇宙处于动态平衡状态。就是说,宇宙既不膨胀,也不收缩,或者说宇宙既膨胀又收缩,但是,膨胀和收缩处于动态平衡状态。
8. 宇宙以等角螺线的方式展开
时空阶梯理论建立之初,假设宇宙的展开是以等角螺旋的方式展开 [14],这次计算行星远离太阳的具体数据,更加证明这个假设是对的,不仅如此,这个等角螺线的展开方式,还是以量子化的方式展开的,
膨胀系数公式
中,n = 1时,是水星的膨胀系数,n = 2
时,是金星的膨胀系数,n = 3时,是地球的膨胀系数,n = 4时,是火星的膨胀系数,n = 5时,是木星的膨胀系数,n = 6时,是土星的膨胀系数,n = 7时,是天王星的膨胀系数,n = 8时,是海王星的膨胀系数,等等。
在大自然中,螺旋几乎无处不在,从银河系之外的宇宙到地球上的飓风,从爬藤植物的藤蔓到蓟、菠萝、松果的外皮,从鹦鹉螺壳上的螺旋花纹到向日葵的种子排列,从人体细胞内在的螺旋结构到外在的螺旋芦荟,等等,动物、植物、人体、天体中都有着神奇的螺旋结构。
以上种种螺旋结构和螺旋现象都是因为宇宙以等角螺旋的方式展开的原因,既然整个宇宙都是以等角螺旋的方式展开,那么宇宙内的万事万物都有螺旋现象就不奇怪了。其实,这也可以从种种螺旋现象事实证明宇宙是以等角螺旋的方式展开是对的。
9. 总结
月亮远离地球,行星远离太阳,都是源自宇宙正在膨胀,但是,这个膨胀速度和远离的距离受到能气场的收缩制约,所以每年的远离距离不符合哈勃定律。根据时空阶梯理论,建立了一个八大行星远离太阳和月亮远离地球的经验公式,计算结果与实际观测基本符合。在解释这个经验公式的时候,发现了太阳系内有自己的精细结构常数,而这个常数的表达式正是时空阶梯因子的倒数,从而发现时空阶梯理论的力的总公式与量子电动力学的力的解释等效,都是以精细结构常数为基础。这次研究发现了精细结构常数的意义,就是精细结构常数变大(原子收缩),宇宙膨胀,而实际观测也是如此,这是时空阶梯理论的核心内容,而这个核心内容被实际观测证明是正确的。通过这次研究,我们发现哈勃定律是经验定律,需要增加能气场力对这个定律的修正。我们计算太阳系内行星的膨胀速度,就算是对哈勃定律的一种修正。但是,时空阶梯理论的解释有偏差,需要完善和进步。我们相信,随着实际测量的不断精确,我们会发现八大行星远离太阳和月亮远离地球真正的原因的。